Regula fazelor
Substanțe pure (un singur component)Edit
Pentru substanțele pure C = 1 astfel încât F = 3 – P. Într-o condiție de fază unică (P = 1) a unui sistem de componente pure, două variabile (F = 2), cum ar fi temperatura și presiunea, pot fi alese independent pentru a fi orice pereche de valori compatibile cu faza. Cu toate acestea, dacă combinația de temperatură și presiune variază până la un punct în care componenta pură suferă o separare în două faze (P = 2), F scade de la 2 la 1. Atunci când sistemul intră în regiunea bifazică, nu mai este posibil să se controleze independent temperatura și presiunea.
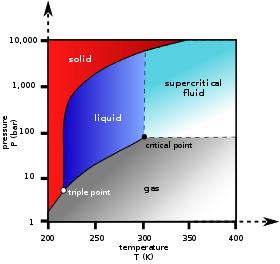
În diagrama de fază din dreapta, curba de graniță dintre regiunile lichidă și gazoasă trasează constrângerea dintre temperatură și presiune atunci când sistemul monocomponent s-a separat în fazele lichidă și gazoasă la echilibru. Singura modalitate de a crește presiunea pe linia celor două faze este prin creșterea temperaturii. Dacă temperatura este scăzută prin răcire, o parte din gaz se condensează, scăzând presiunea. De-a lungul ambelor procese, temperatura și presiunea rămân în relația prezentată de această curbă limită, cu excepția cazului în care una dintre faze este consumată în întregime prin evaporare sau condensare, sau dacă nu se atinge punctul critic. Atâta timp cât există două faze, există un singur grad de libertate, care corespunde poziției de-a lungul curbei frontierei de fază.
Punctul critic este punctul negru de la capătul frontierei lichid-gaz. Pe măsură ce se apropie de acest punct, fazele lichidă și gazoasă devin progresiv mai asemănătoare până când, la punctul critic, nu mai există o separare în două faze. Deasupra punctului critic și departe de curba frontierei de fază, F = 2, iar temperatura și presiunea pot fi controlate independent. Prin urmare, există o singură fază, iar aceasta are proprietățile fizice ale unui gaz dens, dar se mai numește și fluid supercritic.
Dintre celelalte două curbe de frontieră, una este curba de frontieră solid-lichid sau curba punctului de topire, care indică condițiile de echilibru între aceste două faze, iar cealaltă, la temperaturi și presiuni mai mici, este curba de frontieră solid-gaz.
Inclusiv pentru o substanță pură, este posibil ca trei faze, cum ar fi solidul, lichidul și vaporii, să existe împreună în echilibru (P = 3). Dacă există doar un singur component, nu există grade de libertate (F = 0) atunci când există trei faze. Prin urmare, într-un sistem cu un singur component, acest amestec trifazic poate exista doar la o singură temperatură și presiune, care este cunoscută sub numele de punct triplu. Aici există două ecuații μsol(T, p) = μliq(T, p) = μvap(T, p), care sunt suficiente pentru a determina cele două variabile T și p. În diagrama pentru CO2, punctul triplu este punctul în care se întâlnesc fazele solidă, lichidă și gazoasă, la 5,2 bar și 217 K. De asemenea, este posibil ca și alte seturi de faze să formeze un punct triplu, de exemplu, în sistemul apei există un punct triplu în care pot coexista gheața I, gheața III și lichidul.
Dacă patru faze ale unei substanțe pure ar fi în echilibru (P = 4), regula fazelor ar da F = -1, ceea ce nu are sens, deoarece nu pot exista -1 variabile independente. Acest lucru explică faptul că patru faze ale unei substanțe pure (cum ar fi gheața I, gheața III, apa lichidă și vaporii de apă) nu se găsesc în echilibru la nicio temperatură și presiune. În ceea ce privește potențialele chimice, există acum trei ecuații care, în general, nu pot fi satisfăcute de nicio valoare a celor două variabile T și p, deși, în principiu, ar putea fi rezolvate într-un caz special în care o ecuație este dependentă din punct de vedere matematic de celelalte două. Cu toate acestea, în practică, coexistența mai multor faze decât este permisă de regula fazelor înseamnă, în mod normal, că fazele nu sunt toate în echilibru real.
Sisteme cu doi componențiEdit
Pentru amestecuri binare de doi componenți independenți din punct de vedere chimic, C = 2, astfel încât F = 4 – P. În plus față de temperatură și presiune, celălalt grad de libertate este compoziția fiecărei faze, adesea exprimată ca fracție molară sau fracție masică a unui component.

Ca exemplu, considerați sistemul format din două lichide complet miscibile, cum ar fi toluenul și benzenul, în echilibru cu vaporii lor. Acest sistem poate fi descris printr-o diagramă a punctului de fierbere care arată compoziția (fracția molară) a celor două faze în echilibru în funcție de temperatură (la o presiune fixă).
Cele patru variabile termodinamice care pot descrie sistemul includ temperatura (T), presiunea (p), fracția molară a componentei 1 (toluen) în faza lichidă (x1L) și fracția molară a componentei 1 în faza de vapori (x1V). Cu toate acestea, deoarece sunt prezente două faze (P = 2) în echilibru, numai două dintre aceste variabile pot fi independente (F = 2). Acest lucru se datorează faptului că cele patru variabile sunt constrânse de două relații: egalitatea potențialelor chimice ale toluenului lichid și ale toluenului în stare de vapori și egalitatea corespunzătoare pentru benzen.
Pentru T și p date, vor exista două faze în echilibru atunci când compoziția globală a sistemului (punctul sistemului) se situează între cele două curbe. O linie orizontală (izotermă sau linie de legătură) poate fi trasată prin orice astfel de punct al sistemului și intersectează curba pentru fiecare fază la compoziția sa de echilibru. Cantitatea fiecărei faze este dată de regula pârghiei (exprimată în variabila corespunzătoare axei x, aici fracția molară).
Pentru analiza distilării fracționate, se consideră în schimb că cele două variabile independente sunt compoziția fazei lichide (x1L) și presiunea. În acest caz, regula fazelor implică faptul că temperatura de echilibru (punctul de fierbere) și compoziția în fază de vapori sunt determinate.
Diagramele de fază lichid-vapori pentru alte sisteme pot avea azeotropi (maxime sau minime) în curbele de compoziție, dar aplicarea regulii fazelor rămâne neschimbată. Singura diferență este că compozițiile celor două faze sunt egale exact la compoziția azeotropică.
.
Leave a Reply