Phasenregel

Reine Stoffe (eine Komponente)Bearbeiten

Für reine Stoffe ist C = 1, so dass F = 3 – P. In einem einphasigen (P = 1) Zustand eines Systems aus reinen Komponenten können zwei Variablen (F = 2), wie Temperatur und Druck, unabhängig voneinander so gewählt werden, dass sie ein beliebiges Wertepaar darstellen, das der Phase entspricht. Wenn jedoch die Temperatur- und Druckkombination bis zu einem Punkt reicht, an dem die reine Komponente eine Trennung in zwei Phasen (P = 2) erfährt, sinkt F von 2 auf 1. Wenn das System in den Zweiphasenbereich eintritt, ist es nicht mehr möglich, Temperatur und Druck unabhängig voneinander zu steuern.

Druck-Temperatur-Phasendiagramm von Kohlendioxid, das den Tripelpunkt und den kritischen Punkt von Kohlendioxid zeigt

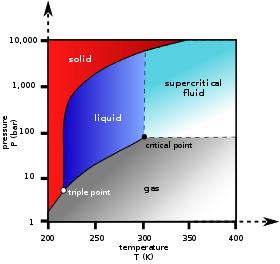
Im Phasendiagramm auf der rechten Seite zeigt die Grenzkurve zwischen dem Flüssigkeits- und dem Gasbereich die Beschränkung zwischen Temperatur und Druck, wenn sich das Einkomponentensystem im Gleichgewicht in eine flüssige und eine gasförmige Phase getrennt hat. Die einzige Möglichkeit, den Druck auf der Zweiphasenlinie zu erhöhen, besteht in einer Erhöhung der Temperatur. Wird die Temperatur durch Abkühlung gesenkt, kondensiert ein Teil des Gases, wodurch der Druck sinkt. Bei beiden Prozessen bleiben Temperatur und Druck in der durch diese Grenzkurve dargestellten Beziehung, es sei denn, eine Phase wird durch Verdampfung oder Kondensation vollständig verbraucht oder der kritische Punkt wird erreicht. Solange es zwei Phasen gibt, gibt es nur einen Freiheitsgrad, der der Position entlang der Phasengrenzkurve entspricht.

Der kritische Punkt ist der schwarze Punkt am Ende der Flüssigkeits-Gas-Grenze. Je mehr man sich diesem Punkt nähert, desto ähnlicher werden sich die flüssige und die gasförmige Phase, bis es am kritischen Punkt keine Trennung in zwei Phasen mehr gibt. Oberhalb des kritischen Punktes und abseits der Phasengrenzkurve ist F = 2 und Temperatur und Druck können unabhängig voneinander geregelt werden. Es gibt also nur eine Phase, die die physikalischen Eigenschaften eines dichten Gases hat, aber auch als überkritisches Fluid bezeichnet wird.

Von den anderen beiden Grenzkurven ist eine die Fest-Flüssig-Grenze oder Schmelzpunktkurve, die die Bedingungen für das Gleichgewicht zwischen diesen beiden Phasen angibt, und die andere bei niedrigerer Temperatur und niedrigerem Druck ist die Fest-Gas-Grenze.

Selbst bei einer reinen Substanz ist es möglich, dass drei Phasen, z. B. fest, flüssig und dampfförmig, im Gleichgewicht miteinander existieren (P = 3). Wenn es nur eine Komponente gibt, gibt es bei drei Phasen keine Freiheitsgrade (F = 0). Daher kann dieses Dreiphasengemisch in einem Einkomponentensystem nur bei einer einzigen Temperatur und einem einzigen Druck existieren, was als Tripelpunkt bezeichnet wird. Hier gibt es zwei Gleichungen μsol(T, p) = μliq(T, p) = μvap(T, p), die ausreichen, um die beiden Variablen T und p zu bestimmen. Im Diagramm für CO2 ist der Tripelpunkt der Punkt, an dem die feste, die flüssige und die gasförmige Phase zusammenkommen, bei 5,2 bar und 217 K. Es ist auch möglich, dass andere Phasensätze einen Tripelpunkt bilden, z. B. gibt es im System Wasser einen Tripelpunkt, in dem Eis I, Eis III und Flüssigkeit koexistieren können.

Wenn vier Phasen eines reinen Stoffes im Gleichgewicht wären (P = 4), würde die Phasenregel F = -1 ergeben, was sinnlos ist, da es keine -1 unabhängigen Variablen geben kann. Dies erklärt die Tatsache, dass vier Phasen einer reinen Substanz (wie Eis I, Eis III, flüssiges Wasser und Wasserdampf) bei keiner Temperatur und keinem Druck im Gleichgewicht sind. In Bezug auf die chemischen Potenziale gibt es nun drei Gleichungen, die im Allgemeinen nicht durch beliebige Werte der beiden Variablen T und p erfüllt werden können, obwohl sie im Prinzip in einem speziellen Fall gelöst werden könnten, in dem eine Gleichung mathematisch von den beiden anderen abhängt. In der Praxis bedeutet jedoch die Koexistenz von mehr Phasen, als die Phasenregel zulässt, normalerweise, dass sich die Phasen nicht alle im echten Gleichgewicht befinden.

ZweikomponentensystemeBearbeiten

Für binäre Gemische aus zwei chemisch unabhängigen Komponenten gilt C = 2, so dass F = 4 – P. Neben Temperatur und Druck ist der andere Freiheitsgrad die Zusammensetzung jeder Phase, die oft als Molen- oder Massenanteil einer Komponente ausgedrückt wird.

Siedepunktdiagramm

Betrachten wir als Beispiel das System zweier vollständig mischbarer Flüssigkeiten wie Toluol und Benzol, die mit ihren Dämpfen im Gleichgewicht sind. Dieses System kann durch ein Siedepunktsdiagramm beschrieben werden, das die Zusammensetzung (Molenbruch) der beiden Phasen im Gleichgewicht als Funktion der Temperatur (bei einem festen Druck) zeigt.

Vier thermodynamische Variablen, die das System beschreiben können, sind Temperatur (T), Druck (p), Molenbruch der Komponente 1 (Toluol) in der flüssigen Phase (x1L) und Molenbruch der Komponente 1 in der Dampfphase (x1V). Da jedoch zwei Phasen im Gleichgewicht vorhanden sind (P = 2), können nur zwei dieser Variablen unabhängig sein (F = 2). Dies liegt daran, dass die vier Variablen durch zwei Beziehungen eingeschränkt werden: die Gleichheit der chemischen Potenziale von flüssigem Toluol und Toluoldampf und die entsprechende Gleichheit für Benzol.

Bei gegebenem T und p gibt es zwei Phasen im Gleichgewicht, wenn die Gesamtzusammensetzung des Systems (Systempunkt) zwischen den beiden Kurven liegt. Eine horizontale Linie (Isotherme oder Verbindungslinie) kann durch jeden solchen Systempunkt gezogen werden und schneidet die Kurve für jede Phase bei ihrer Gleichgewichtszusammensetzung. Die Menge jeder Phase ist durch die Hebelregel gegeben (ausgedrückt in der Variablen, die der x-Achse entspricht, hier der Molenbruch).

Für die Analyse der fraktionierten Destillation werden die beiden unabhängigen Variablen stattdessen als Zusammensetzung der flüssigen Phase (x1L) und Druck betrachtet. In diesem Fall impliziert die Phasenregel, dass die Gleichgewichtstemperatur (Siedepunkt) und die Dampfphasenzusammensetzung bestimmt werden.

Flüssig-Dampf-Phasendiagramme für andere Systeme können Azeotrope (Maxima oder Minima) in den Zusammensetzungskurven aufweisen, aber die Anwendung der Phasenregel ist unverändert. Der einzige Unterschied besteht darin, dass die Zusammensetzungen der beiden Phasen genau bei der azeotropen Zusammensetzung gleich sind.