相の法則

純物質（一成分）編

純物質の場合 F = 3 – PとなるようにC = 1。純成分系の単相（P = 1）条件では、温度と圧力などの2変数（F = 2）は独立して相と一致する任意の値のペアで選ぶことができる。 しかし、温度と圧力の組み合わせが、純成分が2相に分離する（P = 2）ところまで及ぶと、Fは2から1へと減少する。

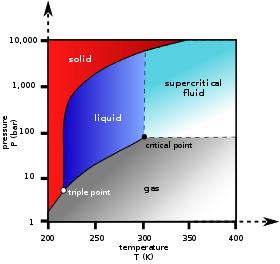
二酸化炭素の三重点と臨界点を示す圧力-温度相図

右の相図において、液体領域と気体領域の境界曲線は単一成分系が平衡状態で液相と気相に分離したときの温度-圧力間の拘束をマッピングしたもので、この境界曲線は液体相が気相に分離したときの温度-圧力間の境界を表す。 二相線上の圧力を上げるには、温度を上げるしかない。 冷却して温度を下げれば、気体の一部が凝縮し、圧力が下がる。 いずれの過程でも、蒸発や凝縮で一方の相が完全に消費されるか、臨界点に達しない限り、温度と圧力はこの境界曲線で示される関係に保たれる。 2つの相がある限り、自由度は1つしかなく、それは相境界曲線に沿った位置に対応する。

臨界点は液相気相境界の端にある黒い点である。 この点に近づくと、液相と気相は徐々に似てきて、臨界点ではもはや2相に分かれることはない。 臨界点以上、相境界曲線から離れるとF=2となり、温度と圧力は独立に制御できるようになる。

他の2つの境界曲線のうち、1つは固液境界または融点曲線で、これらの2相の間の平衡条件を示し、より低い温度と圧力でのもう1つは固気境界である。

純粋な物質であっても、固体、液体、蒸気といった三相が平衡に存在することがある（P=3）。 成分が1つしかない場合、3相が存在しても自由度はない(F=0)。 したがって、単成分の系では、この三相混合物は単一の温度と圧力にしか存在できず、これを三重点という。 ここで、2つの方程式μsol(T, p) = μliq(T, p) = μvap(T, p)があり、これらは2つの変数Tとpを決めるのに十分である。CO2の図では、固相、液相、気相が一緒になる点が三重点で、5.2気圧、217Kである。 例えば水系では氷I、氷III、液体が共存する三重点がある。

純物質の4相が平衡状態（P=4）であれば、位相律はF=-1となるが、独立変数が-1であるはずがないので意味がない。 これは純物質の4相（氷Ⅰ、氷Ⅲ、水、水蒸気など）がどの温度、圧力でも平衡にならないことを説明するものである。 化学ポテンシャルの観点からは、3つの方程式が存在し、これらは一般に2つの変数Tとpの値によっては満たすことができない。ただし、1つの方程式が他の2つの方程式に数学的に依存している特殊なケースでは、原理的に解くことができるかもしれない。

二成分系編集

化学的に独立な二成分の二元混合物では、C=2なのでF=4 – Pとなる。 温度と圧力に加えて、もう一つの自由度は各相の組成で、しばしば一方の成分のモル分率や質量分率で表される。

沸点図

例として、トルエンとベンゼンなどの完全に混和した2液と、その蒸気の平衡系について考えてみよう。 この系は、平衡状態にある2相の組成（モル分率）を温度（固定圧力）の関数として示す沸点図によって記述することができる。

この系を記述できる熱力学変数には、温度（T）、圧力（p）、液相中の成分1（トルエン）のモル分率（x1L）、気相中の成分1のモル分率（x1V）などがある。 しかし、平衡状態では2つの相が存在する（P = 2）ので、これらの変数のうち2つだけが独立である（F = 2）ことができる。 これは4つの変数が、液体トルエンとトルエンベーパーの化学ポテンシャルの等式と、それに対応するベンゼンの等式という2つの関係によって制約されているからです。

与えられたTとpに対して、系の全体組成（系点）が2つの曲線の間にあるとき、平衡状態で2相が存在することになります。 このような系点を通る水平線(等温線またはタイライン)を引くと、各相の平衡組成で曲線と交差する。 各相の量はてこの法則（x軸に対応する変数、ここではモル分率で表す）で与えられる。

分留の解析では、代わりに液相組成（x1L）と圧力という二つの独立変数が考えられている。

他の系の液-蒸気相図では、組成曲線に共沸点（最大または最小）がある場合があるが、位相則の適用に変わりはない。 唯一の違いは、2つの相の組成が共沸組成で正確に等しくなることである

。