Règle de phase
Substances pures (un composant)Edit
Pour les substances pures C = 1 de sorte que F = 3 – P. Dans une condition de phase unique (P = 1) d’un système de composants purs, deux variables (F = 2), telles que la température et la pression, peuvent être choisies indépendamment pour être n’importe quelle paire de valeurs compatibles avec la phase. Cependant, si la combinaison de température et de pression s’étend jusqu’à un point où le composant pur subit une séparation en deux phases (P = 2), F diminue de 2 à 1. Lorsque le système entre dans la région biphasée, il ne devient plus possible de contrôler indépendamment la température et la pression.
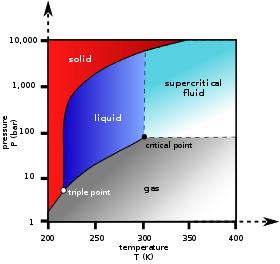
Dans le diagramme de phase à droite, la courbe limite entre les régions liquide et gazeuse cartographie la contrainte entre la température et la pression lorsque le système à un seul composant s’est séparé en phases liquide et gazeuse à l’équilibre. La seule façon d’augmenter la pression sur la ligne à deux phases est d’augmenter la température. Si la température est diminuée par refroidissement, une partie du gaz se condense, ce qui diminue la pression. Tout au long des deux processus, la température et la pression restent dans la relation illustrée par cette courbe limite, sauf si une phase est entièrement consommée par évaporation ou condensation, ou si le point critique est atteint. Tant qu’il y a deux phases, il n’y a qu’un seul degré de liberté, qui correspond à la position le long de la courbe de limite de phase.
Le point critique est le point noir à l’extrémité de la limite liquide-gaz. À mesure que l’on s’approche de ce point, les phases liquide et gazeuse se rapprochent progressivement jusqu’à ce que, au point critique, il n’y ait plus de séparation en deux phases. Au-dessus du point critique et à l’écart de la courbe de limite de phase, F = 2 et la température et la pression peuvent être contrôlées indépendamment. Dès lors, il n’y a qu’une seule phase, et elle a les propriétés physiques d’un gaz dense, mais on parle aussi de fluide supercritique.
Parmi les autres courbes à deux limites, l’une est la limite solide-liquide ou courbe du point de fusion qui indique les conditions d’équilibre entre ces deux phases, et l’autre à température et pression plus faibles est la limite solide-gaz.
Même pour une substance pure, il est possible que trois phases, comme le solide, le liquide et la vapeur, puissent exister ensemble en équilibre (P = 3). S’il n’y a qu’un seul composant, il n’y a pas de degrés de liberté (F = 0) lorsqu’il y a trois phases. Par conséquent, dans un système à un seul composant, ce mélange triphasé ne peut exister qu’à une seule température et une seule pression, que l’on appelle un point triple. Il existe ici deux équations μsol(T, p) = μliq(T, p) = μvap(T, p), qui suffisent à déterminer les deux variables T et p. Dans le diagramme du CO2, le point triple est le point où les phases solide, liquide et gazeuse se rejoignent, à 5,2 bars et 217 K. Il est également possible que d’autres ensembles de phases forment un point triple, par exemple dans le système de l’eau, il existe un point triple où la glace I, la glace III et le liquide peuvent coexister.
Si quatre phases d’une substance pure étaient en équilibre (P = 4), la règle des phases donnerait F = -1, ce qui n’a aucun sens, puisqu’il ne peut y avoir -1 variable indépendante. Cela explique le fait que les quatre phases d’une substance pure (comme la glace I, la glace III, l’eau liquide et la vapeur d’eau) ne sont pas en équilibre, quelles que soient la température et la pression. En termes de potentiels chimiques, il y a maintenant trois équations, qui ne peuvent en général pas être satisfaites par n’importe quelles valeurs des deux variables T et p, bien qu’en principe elles puissent être résolues dans un cas spécial où une équation dépend mathématiquement des deux autres. En pratique, cependant, la coexistence de plus de phases que ne le permet la règle des phases signifie normalement que les phases ne sont pas toutes en équilibre réel.
Systèmes à deux composantsModification
Pour les mélanges binaires de deux composants chimiquement indépendants, C = 2 de sorte que F = 4 – P. En plus de la température et de la pression, l’autre degré de liberté est la composition de chaque phase, souvent exprimée en fraction molaire ou en fraction massique d’un composant.

À titre d’exemple, considérons le système de deux liquides complètement miscibles tels que le toluène et le benzène, en équilibre avec leurs vapeurs. Ce système peut être décrit par un diagramme de point d’ébullition qui montre la composition (fraction molaire) des deux phases en équilibre en fonction de la température (à une pression fixe).
Quatre variables thermodynamiques qui peuvent décrire le système comprennent la température (T), la pression (p), la fraction molaire du composant 1 (toluène) dans la phase liquide (x1L), et la fraction molaire du composant 1 dans la phase vapeur (x1V). Cependant, puisque deux phases sont présentes (P = 2) en équilibre, seules deux de ces variables peuvent être indépendantes (F = 2). En effet, les quatre variables sont contraintes par deux relations : l’égalité des potentiels chimiques du toluène liquide et du toluène vapeur, et l’égalité correspondante pour le benzène.
Pour des T et p donnés, il y aura deux phases à l’équilibre lorsque la composition globale du système (point du système) se situe entre les deux courbes. Une ligne horizontale (isotherme ou ligne de liaison) peut être tracée à travers un tel point du système, et coupe la courbe pour chaque phase à sa composition d’équilibre. La quantité de chaque phase est donnée par la règle du levier (exprimée dans la variable correspondant à l’axe des x, ici la fraction molaire).
Pour l’analyse de la distillation fractionnée, on considère plutôt que les deux variables indépendantes sont la composition de la phase liquide (x1L) et la pression. Dans ce cas, la règle de phase implique que la température d’équilibre (point d’ébullition) et la composition de la phase vapeur sont déterminées.
Les diagrammes de phase liquide-vapeur pour d’autres systèmes peuvent avoir des azéotropes (maxima ou minima) dans les courbes de composition, mais l’application de la règle de phase est inchangée. La seule différence est que les compositions des deux phases sont égales exactement à la composition azéotropique.
Leave a Reply