RL – DQN Deep Q-network

Pot juca calculatoarele jocuri video ca un om? În 2015, DQN a învins experți umani în multe jocuri Atari. Dar, odată ajuns la jocuri complexe de strategie de război, AI nu se descurcă prea bine. În 2017, o echipă de profesioniști a învins cu ușurință un program DeepMind AI în Starcraft 2.
Cum este citat din lucrarea DeepMind:
Este o problemă multi-agent cu mai mulți jucători care interacționează; există informații imperfecte din cauza unei hărți observate parțial; are un spațiu de acțiune mare care implică selectarea și controlul a sute de unități; are un spațiu de stare mare care trebuie observat numai din planurile de caracteristici de intrare brute; și are o atribuire întârziată a creditelor care necesită strategii pe termen lung pe mii de pași.
Să reîncepem călătoria noastră înapoi la rețeaua Deep Q-Network DQN. În jocul Seaquest de mai jos, DQN învață cum să citească scorurile, să împuște inamicul și să salveze scafandrii din imaginile brute, de una singură. Ea descoperă, de asemenea, cunoștințe la care ne putem referi ca strategie, cum ar fi, când să aducem submarinul la suprafață pentru oxigen.

Învățarea Q învață funcția acțiune-valoare Q(s, a): cât de bine este să iei o acțiune la o anumită stare. De exemplu, pentru poziția pe tabla de joc de mai jos, cât de bine este să muți pionul cu doi pași înainte. La propriu, atribuim o valoare scalară asupra beneficiului de a face o astfel de mutare.
Q se numește funcția acțiune-valoare (sau funcția Q-valoare în acest articol).

În învățarea Q, construim un tabel de memorie Q pentru a stoca valorile Q pentru toate combinațiile posibile de s și a. Dacă sunteți un jucător de șah, acesta este foaia de trișat pentru cea mai bună mutare. În exemplul de mai sus, ne putem da seama că mutarea pionului cu 2 pași înainte are cele mai mari valori Q față de toate celelalte. (Consumul de memorie va fi prea mare pentru jocul de șah. Dar haideți să rămânem cu această abordare un pic mai mult timp.)
Tehnic vorbind, eșantionăm o acțiune din starea curentă. Aflăm recompensa R (dacă există) și noua stare s’ (noua poziție pe tablă). Din tabelul de memorie, determinăm următoarea acțiune a’ care trebuie efectuată și care are maximul Q(s’, a’).
Într-un joc video, obținem puncte (recompense) dacă doborâm inamicul. Într-un joc de șah, recompensa este +1 atunci când câștigăm sau -1 dacă pierdem. Așadar, se oferă o singură recompensă și este nevoie de ceva timp pentru a o obține.
Învățarea Q se referă la crearea foii de înșelăciune Q.

Potem să luăm o singură mutare a și să vedem ce recompensă R putem obține. Acest lucru creează o privire înainte cu un singur pas. R + Q(s’, a’) devine ținta pe care dorim să o fie Q(s, a). De exemplu, să spunem că toate valorile Q sunt egale cu unu acum. Dacă mișcăm joystick-ul spre dreapta și obținem 2 puncte, vrem să apropiem Q(s, a) de 3 (adică 2 + 1).

Pe măsură ce continuăm să jucăm, menținem o medie curentă pentru Q. Valorile se vor îmbunătăți și, cu câteva trucuri, valorile lui Q vor converge.
Algoritmul de învățare a lui Q
În cele ce urmează este algoritmul de ajustare a lui Q cu recompensele eșantionate. Dacă γ (factorul de actualizare este mai mic decât unu, există o șansă bună ca Q să converge.

Cu toate acestea, dacă combinațiile de stări și acțiuni sunt prea mari, memoria și necesarul de calcul pentru Q vor fi prea mari. Pentru a rezolva acest aspect, trecem la o rețea profundă Q (DQN) pentru a aproxima Q(s, a). Algoritmul de învățare se numește Deep Q-learning. Cu noua abordare, generalizăm aproximarea funcției de valoare Q, mai degrabă decât să ne amintim soluțiile.
Ce provocări întâmpină RL în comparație cu DL?
În învățarea supravegheată, dorim ca datele de intrare să fie i.i.d. (independente și identic distribuite), adică.
- Eșantioanele sunt randomizate între loturi și, prin urmare, fiecare lot are aceeași distribuție a datelor (sau una similară).
- Eșantioanele sunt independente între ele în același lot.
Dacă nu, modelul poate fi supraadaptat pentru o anumită clasă (sau grupuri) de eșantioane la momente diferite și soluția nu va fi generalizată.
În plus, pentru aceeași intrare, eticheta sa nu se schimbă în timp. Acest tip de condiție stabilă pentru intrare și ieșire asigură condițiile pentru ca învățarea supravegheată să funcționeze bine.
În învățarea prin întărire, atât intrarea cât și ținta se schimbă constant în timpul procesului și fac ca instruirea să fie instabilă.
Țintă instabilă: Construim o rețea profundă pentru a învăța valorile lui Q, dar valorile sale țintă se schimbă pe măsură ce cunoaștem mai bine lucrurile. După cum se arată mai jos, valorile țintă pentru Q depind de Q însuși, urmărim o țintă nestaționară.

i.i.d.: Există o altă problemă legată de corelațiile din cadrul unei traiectorii. În cadrul unei iterații de instruire, actualizăm parametrii modelului pentru a apropia Q(s, a) de adevărul de bază. Aceste actualizări vor avea un impact asupra altor estimări. Atunci când tragem în sus valorile Q în rețeaua profundă, valorile Q din stările înconjurătoare vor fi trase în sus, de asemenea, ca o rețea.

Să spunem că tocmai am obținut o recompensă și ajustăm rețeaua Q pentru a o reflecta. În continuare, facem o altă mișcare. Noua stare va arăta asemănător cu ultima, în special dacă folosim imagini brute pentru a reprezenta stările. Noul Q(s’, a’) recuperat va fi mai mare și noua noastră țintă pentru Q se va deplasa mai sus, de asemenea, indiferent de meritul noii acțiuni. Dacă actualizăm rețeaua cu o secvență de acțiuni pe aceeași traiectorie, aceasta amplifică efectul dincolo de intenția noastră. Acest lucru destabilizează procesul de învățare și sună ca niște câini care își fugăresc coada.
Care este provocarea fundamentală în antrenarea RL? În RL, deseori depindem de politica sau de funcțiile de valoare pentru a eșantiona acțiunile. Cu toate acestea, acest lucru se schimbă frecvent pe măsură ce știm mai bine ce să explorăm. Pe măsură ce desfășurăm jocul, cunoaștem mai bine valorile de adevăr de bază ale stărilor și acțiunilor. Astfel, ieșirile noastre țintă se schimbă și ele. Acum, încercăm să învățăm o cartografiere f pentru o intrare și o ieșire în continuă schimbare!
Din fericire, atât intrarea cât și ieșirea pot converge. Deci, dacă încetinim suficient de mult schimbările atât la intrare cât și la ieșire, am putea avea o șansă de a modela f, permițându-i în același timp să evolueze.
Soluții
Reproducerea experienței: De exemplu, punem ultimul milion de tranziții (sau cadre video) într-un buffer și eșantionăm un mini-lot de eșantioane de dimensiune 32 din acest buffer pentru a antrena rețeaua profundă. Astfel se formează un set de date de intrare care este suficient de stabil pentru antrenare. Pe măsură ce eșantionăm aleatoriu din bufferul de reluare, datele sunt mai independente unele de altele și mai apropiate de i.i.d.
Rețeaua țintă: Creăm două rețele profunde θ- și θ. O folosim pe prima pentru a prelua valorile Q, în timp ce a doua include toate actualizările în procesul de instruire. După, să zicem, 100 000 de actualizări, sincronizăm θ- cu θ. Scopul este de a fixa temporar țintele valorilor Q, astfel încât să nu avem de urmărit o țintă în mișcare. În plus, modificările parametrilor nu au un impact imediat asupra lui θ- și, prin urmare, chiar și intrarea poate să nu fie 100% i.i.d., nu va amplifica în mod incorect efectul său, așa cum s-a menționat anterior.

Atât cu reluarea experienței, cât și cu rețeaua țintă, avem o intrare și o ieșire mai stabile pentru a antrena rețeaua și se comportă mai mult ca o instruire supravegheată.
Reproducerea experienței are cea mai mare îmbunătățire a performanței în DQN. Îmbunătățirea rețelei țintă este semnificativă, dar nu la fel de critică precum reluarea. Dar devine mai importantă atunci când capacitatea rețelei este mică.
Învățare Q profundă cu reluarea experienței
Iată algoritmul:

unde ϕ preprocesează ultimele 4 cadre de imagine pentru a reprezenta starea. Pentru a capta mișcarea, folosim patru cadre pentru a reprezenta o stare.
Detalii de implementare
Funcția de pierdere
Să trecem în revistă alte câteva detalii de implementare pentru a îmbunătăți performanța. DQN utilizează pierderea Huber (curba verde), unde pierderea este pătratică pentru valori mici ale lui a și liniară pentru valori mari.


Introducerea pierderii Huber permite schimbări mai puțin dramatice care adesea afectează RL.
Optimizare
Învățarea RL este sensibilă la metodele de optimizare. Programarea simplă a ratei de învățare nu este suficient de dinamică pentru a face față schimbărilor de intrare în timpul antrenamentului. Multe antrenamente RL utilizează RMSProp sau optimizatorul Adam. DQN este antrenat cu RMSProp. Utilizarea metodei de optimizare avansată în metodele Policy Gradient este, de asemenea, intens studiată.
ϵ-greedy
DQN utilizează ϵ-greedy pentru a selecta prima acțiune.
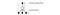
Pentru a îmbunătăți instruirea, ϵ începe la 1 și se recoace la 0.1 sau 0,05 pe parcursul primului milion de cadre folosind următoarea politică.

unde m este numărul de acțiuni posibile. La începutul antrenamentului, selectăm în mod uniform acțiunile posibile, dar pe măsură ce antrenamentul avansează, selectăm mai frecvent acțiunea optimă a*. Acest lucru permite o explorare maximă la început care, în cele din urmă, trece la exploatare.
Dar chiar și în timpul testării, putem menține ϵ la o valoare mică, cum ar fi 0,05. O politică deterministă poate rămâne blocată într-un optim local. O politică nedeterministă ne permite să ieșim pentru o șansă de a ajunge la un optim mai bun.

Arhitectura
Iată arhitectura DQN. Luăm ultimele 4 cadre video anterioare și le introducem în straturi convoluționale urmate de straturi complet conectate pentru a calcula valorile Q pentru fiecare acțiune.

În exemplul de mai jos, dacă nu mișcăm paleta în sus la cadrul 3, vom rata mingea. Așa cum era de așteptat din DQN, valoarea Q a mișcării paletei în sus este mult mai mare în comparație cu alte acțiuni.


Îmbunătățiri aduse DQN
Multe îmbunătățiri sunt aduse DQN. În această secțiune, vom prezenta câteva metode care demonstrează îmbunătățiri semnificative.
Double DQN
În învățarea Q, folosim următoarea formulă pentru valoarea țintă pentru Q.

Cu toate acestea, operația max creează o polarizare pozitivă față de estimările Q.

Din exemplul de mai sus, observăm că max Q(s, a) este mai mare decât valoarea convergentă 1.0. Adică operația max supraestimează Q. Prin teorie și experimente, performanța DQN se îmbunătățește dacă folosim rețeaua online θ pentru a selecta greșit acțiunea și rețeaua țintă θ- pentru a estima valoarea Q.

Reproducere prioritară a experienței
DQN eșantionează în mod uniform tranzițiile din bufferul de reproducere. Cu toate acestea, ar trebui să acordăm mai puțină atenție eșantioanelor care este deja aproape de țintă. Ar trebui să eșantionăm tranzițiile care au un decalaj mare față de țintă:

Prin urmare, putem selecta tranzițiile din memoria tampon
- în funcție de valoarea erorii de mai sus (se aleg mai frecvent tranzițiile cu eroare mai mare) sau
- se clasifică în funcție de valoarea erorii și se selectează în funcție de rang (se alege mai frecvent cea cu rang mai mare).
Pentru detalii cu privire la ecuațiile privind datele de eșantionare, vă rugăm să consultați documentul Prioritized Experience Replay.
Dueling DQN
În Dueling DQN, Q este calculat cu o formulă diferită de mai jos cu funcția de valoare V și o funcție de avantaj de acțiune A, dependentă de stare, de mai jos:

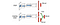
În loc să învățăm Q, folosim două capete separate pentru a calcula V și A. Experimentele empirice arată că performanța se îmbunătățește. DQN actualizează funcția de valoare Q a unei stări numai pentru o anumită acțiune. DQN în duel actualizează V, de care pot profita și alte actualizări Q(s, a’). Astfel, se consideră că fiecare iterație de instruire a DQN Dueling DQN are un impact mai mare.
Neturi zgomotoase pentru explorare
DQN utilizează ϵ-greedy pentru a selecta acțiunile. Alternativ, NoisyNet o înlocuiește prin adăugarea de zgomot parametric la stratul liniar pentru a ajuta explorarea. În NoisyNet, ε-greedy nu este utilizat. Acesta utilizează o metodă greedy pentru a selecta acțiunile din funcția de valoare Q. Dar pentru straturile complet conectate ale aproximatorului Q, adăugăm zgomot parametrizat antrenabil dedesubt pentru a explora acțiunile. Adăugarea de zgomot la o rețea profundă este adesea echivalentă sau mai bună decât adăugarea de zgomot la o acțiune ca cea din metoda ϵ-greedy.

Mai multe gânduri
DQN aparține unei clase importante de RL, și anume învățarea valorilor. În practică, deseori combinăm gradienții de politici cu metodele de învățare a valorilor în rezolvarea problemelor din viața reală.
.
Leave a Reply