RL – DQN Deep Q-network

Wir können einen einzelnen Zug a nehmen und sehen, welche Belohnung R wir bekommen können. Dies erzeugt einen Ein-Schritt-Blick nach vorn. R + Q(s‘, a‘) wird zu dem Ziel, das wir mit Q(s, a) anstreben. Nehmen wir zum Beispiel an, alle Q-Werte sind jetzt gleich eins. Wenn wir den Joystick nach rechts bewegen und 2 Punkte erzielen, wollen wir Q(s, a) näher an 3 (d.h. 2 + 1) heranbringen.

Während wir weiter spielen, halten wir einen laufenden Durchschnitt für Q aufrecht. Die Werte werden besser und mit einigen Tricks konvergieren die Q-Werte.

Q-Lernalgorithmus

Im Folgenden wird der Algorithmus zur Anpassung von Q an die gesampelten Belohnungen beschrieben. Wenn γ (Diskontierungsfaktor) kleiner als eins ist, besteht eine gute Chance, dass Q konvergiert.

Wenn jedoch die Kombinationen von Zuständen und Aktionen zu groß sind, werden der Speicher- und der Rechenbedarf für Q zu hoch. Um dem zu begegnen, wechseln wir zu einem tiefen Netzwerk Q (DQN), um Q(s, a) zu approximieren. Der Lernalgorithmus wird Deep Q-learning genannt. Mit dem neuen Ansatz verallgemeinern wir die Approximation der Q-Wert-Funktion, anstatt uns die Lösungen zu merken.

Welchen Herausforderungen steht RL im Vergleich zu DL gegenüber?

Beim überwachten Lernen wollen wir, dass die Eingabe i.i.d. (unabhängig und identisch verteilt) ist, d.h.

• Die Stichproben werden unter den Stapeln randomisiert und daher hat jeder Stapel die gleiche (oder eine ähnliche) Datenverteilung.
• Die Stichproben sind innerhalb einer Charge unabhängig voneinander.

Andernfalls kann das Modell für einige Klassen (oder Gruppen) von Stichproben zu verschiedenen Zeitpunkten überangepasst sein, und die Lösung wird nicht verallgemeinert.

Darüber hinaus ändert sich die Bezeichnung für dieselbe Eingabe im Laufe der Zeit nicht. Diese Art von stabilen Bedingungen für die Eingabe und die Ausgabe ist die Voraussetzung dafür, dass das überwachte Lernen gut funktioniert.

Beim Reinforcement Learning ändern sich sowohl die Eingabe als auch das Ziel während des Prozesses ständig und machen das Training instabil.

Ziel instabil: Wir bauen ein tiefes Netzwerk auf, um die Werte von Q zu lernen, aber seine Zielwerte ändern sich, wenn wir etwas besser wissen. Wie unten gezeigt, hängen die Zielwerte für Q von Q selbst ab, wir verfolgen ein nicht-stationäres Ziel.

i.i.d.: Es gibt ein weiteres Problem im Zusammenhang mit den Korrelationen innerhalb einer Trajektorie. Innerhalb einer Trainingsiteration aktualisieren wir die Modellparameter, um Q(s, a) näher an die Grundwahrheit zu bringen. Diese Aktualisierungen wirken sich auf andere Schätzungen aus. Wenn wir die Q-Werte im tiefen Netz nach oben ziehen, werden die Q-Werte in den umliegenden Zuständen ebenfalls wie ein Netz nach oben gezogen.

Angenommen, wir haben gerade eine Belohnung erhalten und das Q-Netz entsprechend angepasst. Als nächstes machen wir einen weiteren Zug. Der neue Zustand wird ähnlich aussehen wie der letzte, insbesondere wenn wir Rohbilder zur Darstellung von Zuständen verwenden. Das neu ermittelte Q(s‘, a‘) wird höher sein und unser neues Ziel für Q wird sich ebenfalls nach oben bewegen, unabhängig vom Wert der neuen Aktion. Wenn wir das Netzwerk mit einer Abfolge von Aktionen auf derselben Bahn aktualisieren, wird der Effekt über unsere Absicht hinaus verstärkt. Das destabilisiert den Lernprozess und klingt, als würden Hunde ihren Schwanz jagen.

Was ist die grundlegende Herausforderung beim Training von RL? In RL verlassen wir uns oft auf die Richtlinien- oder Wertfunktionen, um Handlungen zu testen. Dies ändert sich jedoch häufig, da wir besser wissen, was wir erforschen wollen. Während wir das Spiel spielen, wissen wir besser über die wahren Werte von Zuständen und Aktionen Bescheid. Daher ändern sich auch unsere Zielausgaben. Nun versuchen wir, eine Abbildung f für eine sich ständig ändernde Eingabe und Ausgabe zu lernen!

Glücklicherweise können sowohl Eingabe als auch Ausgabe konvergieren. Wenn wir also die Veränderungen von Input und Output ausreichend verlangsamen, haben wir vielleicht eine Chance, f zu modellieren, während wir ihm erlauben, sich zu entwickeln.

Lösungen

Erfahrungen wiederholen: Wir legen zum Beispiel die letzte Million Übergänge (oder Videobilder) in einen Puffer und entnehmen diesem Puffer einen Mini-Stapel von Samples der Größe 32, um das Deep Network zu trainieren. Dies bildet einen Eingabedatensatz, der stabil genug für das Training ist. Da wir nach dem Zufallsprinzip Stichproben aus dem Wiedergabepuffer ziehen, sind die Daten unabhängiger voneinander und näher am i.i.d.

Zielnetzwerk: Wir erstellen zwei tiefe Netzwerke θ- und θ. Wir verwenden das erste, um Q-Werte abzurufen, während das zweite alle Aktualisierungen in das Training einbezieht. Nach etwa 100.000 Aktualisierungen synchronisieren wir θ- mit θ. Der Zweck besteht darin, die Q-Wert-Ziele vorübergehend zu fixieren, damit wir kein bewegliches Ziel zu verfolgen haben. Außerdem wirken sich Parameteränderungen nicht sofort auf θ- aus, so dass selbst die Eingabe nicht zu 100 % i.i.d. sein kann,

Mit sowohl der Erfahrungswiederholung als auch dem Zielnetz haben wir eine stabilere Eingabe und Ausgabe, um das Netz zu trainieren, und es verhält sich eher wie ein überwachtes Training.

Die Erfahrungswiederholung hat die größte Leistungsverbesserung im DQN. Die Verbesserung des Zielnetzes ist signifikant, aber nicht so kritisch wie die Wiederholung. Sie wird jedoch wichtiger, wenn die Kapazität des Netzes gering ist.

Deep Q-learning with experience replay

Hier ist der Algorithmus:

wobei ϕ die letzten 4 Bildframes vorverarbeitet, um den Zustand darzustellen. Um Bewegungen zu erfassen, verwenden wir vier Bilder, um einen Zustand zu repräsentieren.

Implementierungsdetails

Verlustfunktion

Lassen Sie uns ein paar weitere Implementierungsdetails durchgehen, um die Leistung zu verbessern. DQN verwendet den Huber-Verlust (grüne Kurve), wobei der Verlust für kleine Werte von a quadratisch und für große Werte linear ist.

Die Einführung des Huber-Verlustes ermöglicht weniger drastische Änderungen, die RL oft schaden.

Optimierung

RL-Training ist empfindlich gegenüber Optimierungsmethoden. Ein einfacher Lernratenplan ist nicht dynamisch genug, um Änderungen der Eingaben während des Trainings zu verarbeiten. Viele RL-Trainings verwenden RMSProp oder Adam-Optimierer. DQN wird mit RMSProp trainiert. Die Verwendung von fortschrittlichen Optimierungsmethoden in Policy-Gradient-Methoden wird ebenfalls intensiv untersucht.

ϵ-greedy

DQN verwendet ϵ-greedy, um die erste Aktion auszuwählen.

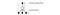
Um das Training zu verbessern, beginnt ϵ bei 1 und glüht auf 0.1 oder 0,05 über die erste Million Frames unter Verwendung der folgenden Strategie.

wobei m die Anzahl der möglichen Aktionen ist. Zu Beginn des Trainings wählen wir die möglichen Aktionen gleichmäßig aus, aber mit dem Fortschreiten des Trainings wählen wir die optimale Aktion a* häufiger aus. Dies ermöglicht eine maximale Exploration zu Beginn, die schließlich in eine Ausnutzung übergeht.

Aber auch während des Testens können wir ϵ auf einem kleinen Wert wie 0,05 halten. Eine deterministische Politik kann in einem lokalen Optimum stecken bleiben. Eine nicht-deterministische Politik erlaubt es uns, auszubrechen, um ein besseres Optimum zu erreichen.

Architektur

Hier ist die DQN-Architektur. Wir nehmen die letzten 4 vorherigen Videobilder und speisen sie in Faltungsschichten ein, gefolgt von vollständig verbundenen Schichten, um die Q-Werte für jede Aktion zu berechnen.

Im folgenden Beispiel werden wir den Ball verfehlen, wenn wir das Paddel bei Bild 3 nicht nach oben bewegen. Wie von der DQN erwartet, ist der Q-Wert beim Hochziehen des Schlägers im Vergleich zu anderen Aktionen viel höher.

Verbesserungen des DQN

Viele Verbesserungen wurden am DQN vorgenommen. In diesem Abschnitt werden einige Methoden vorgestellt, die signifikante Verbesserungen darstellen.

Doppel-DQN

Beim Q-Lernen wird die folgende Formel für den Zielwert für Q verwendet.

Die Max-Operation erzeugt jedoch eine positive Verzerrung der Q-Schätzungen.

Aus dem obigen Beispiel geht hervor, dass max Q(s, a) höher ist als der konvergierte Wert 1.0. d.h. die max-Operation überschätzt Q. Nach Theorie und Experimenten verbessert sich die DQN-Leistung, wenn wir das Online-Netzwerk θ zur gierigen Auswahl der Aktion und das Zielnetzwerk θ- zur Schätzung des Q-Wertes verwenden.

Priorisierte Erfahrungswiedergabe

DQN sampelt gleichmäßig Übergänge aus dem Wiedergabepuffer. Wir sollten jedoch weniger auf Übergänge achten, die sich bereits in der Nähe des Ziels befinden. Wir sollten Übergänge abtasten, die einen großen Abstand zum Ziel haben:

Daher können wir Übergänge aus dem Puffer

• auf der Grundlage des obigen Fehlerwerts auswählen (Übergänge mit höherem Fehler häufiger auswählen), oder
• sie nach dem Fehlerwert ordnen und nach Rang auswählen (den mit dem höheren Rang häufiger auswählen).

Einzelheiten zu den Gleichungen für Stichprobendaten finden Sie in dem Dokument Priorisierte Erfahrungswiederholung.

Duelles DQN

Im Duellierenden DQN wird Q mit einer anderen Formel unten mit der Wertfunktion V und einer zustandsabhängigen Aktionsvorteilsfunktion A unten berechnet:

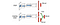
Anstatt Q zu lernen, verwenden wir zwei separate Köpfe zur Berechnung von V und A. Empirische Experimente zeigen, dass sich die Leistung verbessert. DQN aktualisiert die Q-Wert-Funktion eines Zustands nur für eine bestimmte Aktion. Dueling DQN aktualisiert V, was andere Q(s, a‘)-Updates ebenfalls nutzen können. Daher wird davon ausgegangen, dass jede Dueling-DQN-Trainingsiteration eine größere Auswirkung hat.

Noisy Nets for Exploration

DQN verwendet ϵ-greedy zur Auswahl von Aktionen. Alternativ dazu ersetzt NoisyNet diese Methode, indem es parametrisches Rauschen zur linearen Schicht hinzufügt, um die Exploration zu unterstützen. In NoisyNet wird ε-greedy nicht verwendet. Es verwendet eine gierige Methode, um Aktionen aus der Q-Wert-Funktion auszuwählen. Für die vollständig verbundenen Schichten des Q-Approximators fügen wir jedoch trainierbares parametrisches Rauschen hinzu, um Aktionen zu erkunden. Das Hinzufügen von Rauschen zu einem tiefen Netz ist oft gleichwertig oder besser als das Hinzufügen von Rauschen zu einer Aktion wie bei der ϵ-greedy-Methode.

Weitere Gedanken

DQN gehört zu einer wichtigen Klasse von RL, nämlich dem Value-Learning. In der Praxis kombinieren wir bei der Lösung realer Probleme oft Policy-Gradienten mit Value-Learning-Methoden.