Restricted Boltzmann Machines – Simplified
Co to są Restricted Boltzmann Machines?
RBM są dwuwarstwowymi sztucznymi sieciami neuronowymi o zdolnościach generatywnych. Mają one zdolność uczenia się rozkładu prawdopodobieństwa na swoim zbiorze danych wejściowych. RBM zostały wynalezione przez Geoffrey’a Hintona i mogą być używane do redukcji wymiarowości, klasyfikacji, regresji, filtrowania kolaboracyjnego, uczenia cech i modelowania tematycznego.
RBM są specjalną klasą maszyn Boltzmanna i są ograniczone pod względem połączeń pomiędzy jednostkami widocznymi i ukrytymi. Ułatwia to ich implementację w porównaniu z maszynami Boltzmanna. Jak wspomniano wcześniej, są one dwuwarstwową siecią neuronową (jedna to warstwa widoczna, a druga to warstwa ukryta) i te dwie warstwy są połączone grafem w pełni dwudzielnym. Oznacza to, że każdy węzeł w warstwie widocznej jest połączony z każdym węzłem w warstwie ukrytej, ale żadne dwa węzły w tej samej grupie nie są połączone ze sobą. To ograniczenie pozwala na zastosowanie bardziej wydajnych algorytmów treningowych niż te, które są dostępne dla ogólnej klasy maszyn Boltzmanna, w szczególności gradientowego algorytmu dywergencji kontrastowej.
Zwężona maszyna Boltzmanna wygląda tak:
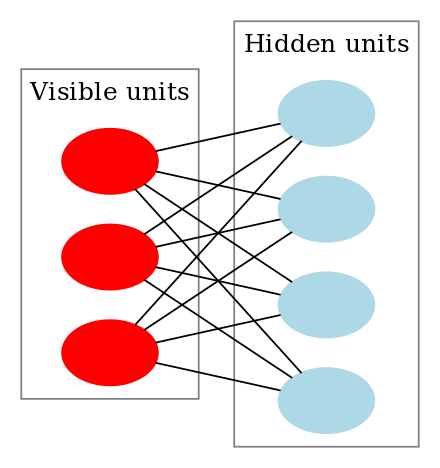
Jak działają ograniczone maszyny Boltzmanna?
W RBM mamy symetryczny graf dwudzielny, w którym żadne dwie jednostki w obrębie tej samej grupy nie są połączone. Wiele RBM może być również stacked i mogą być dostrojone poprzez proces zejścia gradientowego i wstecznej propagacji. Taka sieć nazywana jest Deep Belief Network. Chociaż RBM są sporadycznie używane, większość ludzi w społeczności głębokiego uczenia zaczęła zastępować ich użycie przez General Adversarial Networks lub Variational Autoencoders.
RBM jest Stochastyczną Siecią Neuronową, co oznacza, że każdy neuron będzie miał pewne losowe zachowanie, gdy jest aktywowany. Istnieją dwie inne warstwy jednostek uprzedzenia (ukryte uprzedzenie i widoczne uprzedzenie) w RBM. To jest to, co odróżnia RBM od autoenkoderów. Ukryty bias RBM produkuje aktywację podczas przechodzenia w przód, a widoczny bias pomaga RBM zrekonstruować dane wejściowe podczas przechodzenia w tył. Zrekonstruowane wejście zawsze różni się od rzeczywistego, ponieważ nie ma połączeń między widocznymi jednostkami, a zatem nie ma sposobu na przekazywanie informacji między nimi.

Powyższy obrazek pokazuje pierwszy etap treningu RBM z wieloma wejściami. Dane wejściowe są mnożone przez wagi, a następnie dodawane do błędu systematycznego. Wynik jest następnie przepuszczany przez sigmoidalną funkcję aktywacji, a wyjście określa, czy stan ukryty zostanie aktywowany, czy nie. Wagi będą macierzą z liczbą węzłów wejściowych jako liczbą wierszy i liczbą węzłów ukrytych jako liczbą kolumn. Pierwszy węzeł ukryty otrzyma iloczyn wektorowy wejść pomnożonych przez pierwszą kolumnę wag, zanim zostanie do niego dodany odpowiedni człon diagonalny.
A jeśli zastanawiasz się, czym jest funkcja sigmoidalna, oto wzór:

Więc równanie, które otrzymamy w tym kroku brzmiałoby,
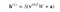
gdzie h(1) i v(0) są odpowiednimi wektorami (macierzami kolumnowymi) dla warstwy ukrytej i widocznej z indeksem górnym jako iteracją (v(0) oznacza wejście, które dostarczamy do sieci), a a jest wektorem nierówności warstwy ukrytej.
(Zauważ, że mamy tu do czynienia z wektorami i macierzami, a nie wartościami jednowymiarowymi.)

Teraz ten obraz pokazuje fazę odwrotną lub fazę rekonstrukcji. Jest to podobne do pierwszego przejścia, ale w przeciwnym kierunku. Równanie wychodzi następująco:
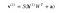
.
Leave a Reply