Restricted Boltzmann Machines – Vereenvoudigd
Wat zijn Restricted Boltzmann Machines?
RBMs zijn een tweelagig kunstmatig neuraal netwerk met generatieve mogelijkheden. Ze hebben de mogelijkheid om een kansverdeling te leren over de set van invoer. RBM’s zijn uitgevonden door Geoffrey Hinton en kunnen worden gebruikt voor dimensionaliteitsreductie, classificatie, regressie, collaborative filtering, feature learning, en topic modeling.
RBM’s zijn een speciale klasse van Boltzmann Machines en ze zijn beperkt in termen van de verbindingen tussen de zichtbare en de verborgen eenheden. Daardoor zijn zij gemakkelijker te implementeren dan Boltzmannmachines. Zoals eerder gezegd, zijn zij een neuraal netwerk met twee lagen (de zichtbare laag en de verborgen laag) en deze twee lagen zijn verbonden door een volledig bipartiete grafiek. Dit betekent dat elk knooppunt in de zichtbare laag verbonden is met elk knooppunt in de verborgen laag, maar dat geen twee knooppunten in dezelfde groep met elkaar verbonden zijn. Deze beperking maakt efficiëntere trainingsalgoritmen mogelijk dan wat beschikbaar is voor de algemene klasse van Boltzmannmachines, in het bijzonder het op gradiënten gebaseerde contrastieve divergentiealgoritme.
Een Restricted Boltzmann Machine ziet er als volgt uit:
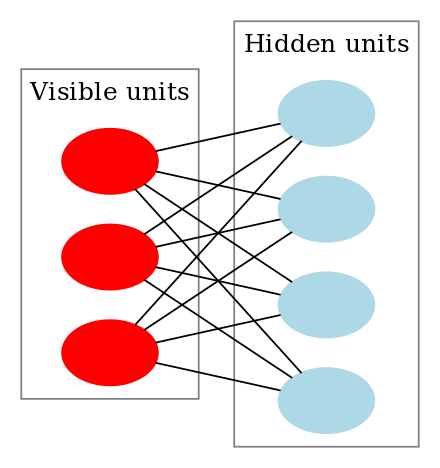
Hoe werken Restricted Boltzmann Machines?
In een RBM hebben we een symmetrische tweeledige grafiek waarin geen twee eenheden binnen dezelfde groep met elkaar verbonden zijn. Meervoudige RBM’s kunnen ook stacked en kunnen worden verfijnd door het proces van gradiëntafdaling en back-propagatie. Een dergelijk netwerk wordt een Deep Belief Network genoemd. Hoewel RBM’s af en toe worden gebruikt, zijn de meeste mensen in de deep-learning gemeenschap begonnen het gebruik ervan te vervangen door General Adversarial Networks of Variational Autoencoders.
RBM is een Stochastisch Neuraal Netwerk, wat betekent dat elk neuron een zeker willekeurig gedrag zal vertonen wanneer het wordt geactiveerd. Er zijn twee andere lagen van bias-eenheden (verborgen bias en zichtbare bias) in een RBM. Dit is wat RBM’s onderscheidt van autoencoders. De verborgen bias van RBM’s produceert de activering tijdens de voorwaartse passage en de zichtbare bias helpt RBM’s de input te reconstrueren tijdens een achterwaartse passage. De gereconstrueerde invoer verschilt altijd van de werkelijke invoer, aangezien er geen verbindingen tussen de zichtbare eenheden zijn en er bijgevolg geen manier is om informatie onderling over te dragen.

De bovenstaande afbeelding toont de eerste stap in het trainen van een RBM met meerdere ingangen. De inputs worden vermenigvuldigd met de gewichten en vervolgens opgeteld bij de bias. Het resultaat wordt vervolgens door een sigmoïde activeringsfunctie geleid en de output bepaalt of de verborgen staat wordt geactiveerd of niet. De gewichten zullen een matrix zijn met het aantal inputknooppunten als het aantal rijen en het aantal verborgen knooppunten als het aantal kolommen. De eerste verborgen knoop ontvangt de vectorvermenigvuldiging van de ingangen, vermenigvuldigd met de eerste kolom van de gewichten, voordat de bijbehorende bias-term eraan wordt toegevoegd.
En als u zich afvraagt wat een sigmoid-functie is, hier is de formule:

Dus de vergelijking die we in deze stap krijgen zou zijn,
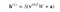
waarbij h(1) en v(0) de overeenkomstige vectoren (kolommatrices) zijn voor de verborgen en de zichtbare lagen met het superscript als de iteratie (v(0) betekent de input die we aan het netwerk geven) en a is de biasvector van de verborgen laag.
(Merk op dat we hier te maken hebben met vectoren en matrices en niet met eendimensionale waarden.)

Nu toont deze afbeelding de omgekeerde fase of de reconstructiefase. Deze is vergelijkbaar met de eerste pas, maar dan in omgekeerde richting. De vergelijking luidt:
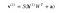
Leave a Reply