Restricted Boltzmann Machines – Simplified
制限付きボルツマンマシンとは?
RBMは生成能力を持つ2層構造の人工神経回路網です。 入力の集合に対する確率分布を学習する能力がある。 RBMはGeoffrey Hintonによって発明され、次元削減、分類、回帰、協調フィルタリング、特徴学習、トピックモデリングに使用できる。
RBMはボルツマンマシンの特殊クラスで、可視ユニットと隠れユニットの間の接続が制限されている。 そのため、ボルツマンマシンと比較すると、実装が容易である。 前述のように、ボルツマンマシンは2層のニューラルネットワーク(一方が可視層、もう一方が隠れ層)で、この2層は完全2部グラフで接続されている。 つまり、可視層のすべてのノードは隠れ層のすべてのノードに接続されているが、同じグループの2つのノードが互いに接続されていることはない。 この制限により、ボルツマンマシンの一般クラスで利用可能なものよりも効率的な学習アルゴリズム、特に勾配に基づくコントラストダイバージェンスアルゴリズムを利用することができる。
制限付きボルツマン マシンは次のようになります。
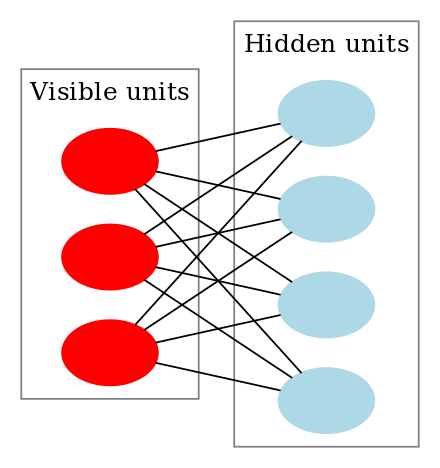
How do Restricted Boltzmann Machines work?
RBM では、同じグループ内の 2 つのユニットは接続しない対称二部グラフが存在します。 複数のRBMもstacked可能で、勾配降下とバックプロパゲーションのプロセスを通じて微調整が可能です。 このようなネットワークはディープ・ビリーフ・ネットワークと呼ばれる。 RBM は時々使用されますが、深層学習コミュニティのほとんどの人は、その使用を一般的な逆説的ネットワークまたは変分オートエンコーダーに置き換え始めています。
RBM は確率的ニューラル ネットワークで、各ニューロンはアクティブになるといくつかのランダムな動作をすることを意味します。 また、RBMではバイアスユニットが2層(隠れバイアスと可視バイアス)になっています。 これがRBMがオートエンコーダーと異なる点である。 隠れバイアスのRBMは前方通過時に活性化を生成し、可視バイアスは後方通過時にRBMが入力を再構成するのに役立つ。

上の画像は、複数の入力でRBMを学習する最初のステップを示したものです。 入力は重みで乗算され、バイアスに加えられます。 その結果はシグモイド活性化関数に渡され、出力によって隠れた状態が活性化されるかどうかが決定されます。 重みは、入力ノードの数を行数、隠れノードの数を列数とする行列となる。 最初の隠れノードには、対応するバイアス項が追加される前に、重みの最初の列によって乗算された入力のベクトル積が送られます。
また、シグモイド関数が何であるか疑問である場合、以下はその公式です。 My Blog
つまり、このステップで得られる方程式は、次のようになります。
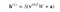
ここで h(1) と v(0) は隠れ層と可視層の対応ベクトルで、上付き文字が反復です( v(0) はネットワークに与える入力)、a は隠れ層のバイアスベクトルです。
(ここではベクトルと行列を扱っており、一次元の値ではないことに注意してください)

さてこの画像では逆相、つまり再構成段階を表しています。 これは最初のパスと似ていますが、逆方向です。 式は次のようになります:
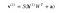
Leave a Reply