RL – DQN Deep Q-network

A számítógépek tudnak úgy játszani videojátékokkal, mint az emberek? 2015-ben a DQN számos Atari-játékban legyőzte az emberi szakértőket. De ha egyszer összetett háborús stratégiai játékokra kerül sor, az AI nem teljesít jól. 2017-ben egy profi csapat könnyedén legyőzte a DeepMind AI programját a Starcraft 2-ben.

A DeepMind tanulmányából idézve:

Ez egy multiágens probléma több játékos interakciójával; tökéletlen információval rendelkezik a részben megfigyelt térkép miatt; nagy akciótérrel rendelkezik, amely több száz egység kiválasztását és irányítását foglalja magában; nagy állapottérrel rendelkezik, amelyet kizárólag nyers bemeneti jellemzősíkok alapján kell megfigyelni; és késleltetett kreditkiosztással rendelkezik, amely több ezer lépés hosszú távú stratégiát igényel.

Kezdjük újra az utazásunkat vissza a Deep Q-Network DQN-hez. Az alábbi Seaquest játékban a DQN a nyers képekből magától megtanulja, hogyan olvassa a pontszámokat, hogyan lője le az ellenséget, és hogyan mentse ki a búvárokat. Olyan ismereteket is felfedez, amelyeket stratégiának nevezhetünk, például, hogy mikor kell a tengeralattjárót oxigénért a felszínre hozni.

A Q-learning megtanulja a Q(s, a) akcióérték-függvényt: hogy egy adott állapotban mennyire jó egy akciót végrehajtani. Például az alábbi táblaállás esetében, hogy mennyire jó a gyalogot két lépést előre lépni. Szó szerint egy skalárértéket rendelünk az ilyen lépés megtételének hasznához.

Q-t akcióérték-függvénynek (vagy ebben a cikkben Q-érték-függvénynek) nevezzük.

A Q-tanulásban egy Q memóriatáblát építünk, amelyben az s és a összes lehetséges kombinációjának Q-értékét tároljuk. Ha sakkozó vagy, ez a legjobb lépés puskája. A fenti példában rájöhetünk, hogy a 2 lépéssel előrébb lépő gyalog mozgatása a legmagasabb Q-értékkel rendelkezik az összes többihez képest. (A memóriafogyasztás túl nagy lesz a sakkjátszma számára. De maradjunk még egy kicsit ennél a megközelítésnél.)

Technikai értelemben az aktuális állapotból mintavételezünk egy akciót. Megtudjuk a jutalmat R (ha van) és az új s’ állapotot (az új táblaállást). A memóriatáblából meghatározzuk a következő a’ akciót, amelyik a maximális Q(s’, a’).

Egy videojátékban az ellenség lelövésével pontokat (jutalmat) szerzünk. Egy sakkjátékban a jutalom +1, ha nyerünk, vagy -1, ha veszítünk. Tehát csak egy jutalom van megadva, és annak megszerzéséhez időre van szükség.

A Q-tanulás arról szól, hogy létrehozzuk a Q puskát.

Megnézzük, hogy egyetlen lépéssel a milyen jutalmat R kaphatunk. Ez egy egylépéses előretekintést hoz létre. R + Q(s’, a’) lesz az a cél, amit Q(s, a)-nak szeretnénk. Tegyük fel például, hogy most minden Q érték egyenlő eggyel. Ha a joystickot jobbra mozgatjuk, és 2 pontot szerzünk, akkor a Q(s, a) értéket közelebb akarjuk vinni a 3-hoz (azaz 2 + 1).

Amíg játszunk, fenntartjuk a Q folyó átlagát. Az értékek egyre jobbak lesznek, és néhány trükkel a Q értékek konvergálni fognak.

Q-tanuló algoritmus

A következő algoritmus a Q-t a mintavételezett jutalmakkal illeszti össze. Ha γ (diszkontfaktor) kisebb, mint egy, akkor jó esély van arra, hogy a Q konvergál.

Ha azonban az állapotok és akciók kombinációi túl nagyok, akkor a Q memória- és számítási igénye túl nagy lesz. Ennek megoldására áttérünk a Q(s, a) közelítésére a Q(s, a) mély hálózatra (DQN). A tanulási algoritmust Deep Q-learningnek nevezzük. Az új megközelítéssel a megoldások megjegyzése helyett a Q-értékfüggvény közelítését általánosítjuk.

Milyen kihívásokkal néz szembe az RL a DL-hez képest?

A felügyelt tanulásban azt akarjuk, hogy a bemenet i.i.d. (független és azonosan elosztott) legyen, azaz:

• A mintákat véletlenszerűen osztjuk szét a tételek között, ezért minden tétel azonos (vagy hasonló) adateloszlással rendelkezik.
• A minták függetlenek egymástól ugyanabban a tételben.

Ha nem, akkor a modell túlillesztett lehet a minták bizonyos osztályára (vagy csoportjaira) különböző időpontokban, és a megoldás nem lesz általánosítható.

Ezeken kívül ugyanazon bemenet esetén a címkéje nem változik idővel. A bemenet és a kimenet ilyen stabil állapota biztosítja a felügyelt tanulás jó teljesítményének feltételét.

A megerősített tanulásban mind a bemenet, mind a cél folyamatosan változik a folyamat során, és instabillá teszi a képzést.

A cél instabil: Építünk egy mélyhálót, hogy megtanulja a Q értékeit, de a célértékei változnak, ahogy jobban megismerjük a dolgokat. Mint alább látható, a Q célértékei magától a Q-tól függnek, nem stacionárius célt kergetünk.

i.i.d.: Van egy másik probléma is, amely a pályán belüli korrelációkkal kapcsolatos. Egy képzési iteráción belül frissítjük a modell paramétereit, hogy a Q(s, a) közelebb kerüljön az alapigazsághoz. Ezek a frissítések hatással lesznek más becslésekre. Amikor a Q-értékeket felfelé húzzuk a mélyhálóban, a környező állapotok Q-értékei is felfelé húzódnak, mint egy háló.

Tegyük fel, hogy éppen egy jutalmat kapunk, és ennek megfelelően módosítjuk a Q-hálót. Ezután újabb lépést teszünk. Az új állapot különösen akkor fog hasonlítani az előzőhöz, ha nyers képeket használunk az állapotok ábrázolására. Az újonnan kinyert Q(s’, a’) magasabb lesz, és az új Q célunk is magasabbra fog mozogni, függetlenül az új akció érdemességétől. Ha a hálózatot azonos pályán futó akciósorozattal frissítjük, az a szándékunkon túlmenően felnagyítja a hatást. Ez destabilizálja a tanulási folyamatot, és úgy hangzik, mintha a kutyák kergetnék a farkukat.

Mi az alapvető kihívás az RL képzésében? Az RL-ben gyakran függünk a politikától vagy az értékfüggvényektől a cselekvések mintavételezéséhez. Ez azonban gyakran változik, mivel egyre jobban tudjuk, hogy mit kell felfedezni. Ahogy játsszuk a játékot, egyre jobban ismerjük az állapotok és akciók alapigazság-értékeit. Így a célkimeneteink is változnak. Most megpróbálunk megtanulni egy f leképezést egy folyamatosan változó bemenetre és kimenetre!

Szerencsés esetben mind a bemenet, mind a kimenet konvergálhat. Tehát ha eléggé lelassítjuk mind a bemenet, mind a kimenet változását, akkor lehet esélyünk arra, hogy úgy modellezzük az f-et, hogy közben hagyjuk fejlődni.

Megoldások

Tapasztalat-visszajátszás: Például az utolsó egymillió átmenetet (vagy videóképet) egy pufferbe tesszük, és ebből a pufferből 32 méretű miniatűr mintákat veszünk a mély hálózat edzéséhez. Ez egy olyan bemeneti adathalmazt képez, amely elég stabil a képzéshez. Mivel véletlenszerűen veszünk mintát a visszajátszási pufferből, az adatok függetlenebbek egymástól és közelebb állnak az i.i.d.

célhálózathoz: Két mély hálózatot hozunk létre θ- és θ. Az elsőt a Q értékek lekérdezésére használjuk, míg a második az összes frissítést tartalmazza a képzésben. Mondjuk 100 000 frissítés után szinkronizáljuk a θ–t a θ-vel. A cél az, hogy ideiglenesen rögzítsük a Q-értékek célpontjait, hogy ne kelljen mozgó célpontot üldöznünk. Ráadásul a paraméterek változásai nem hatnak azonnal a θ- re, ezért még a bemenet sem biztos, hogy 100%-ban i.i.d., nem fogja helytelenül felnagyítani a hatását, ahogy korábban említettük.

A tapasztalatok visszajátszásával és a célhálózattal egyaránt stabilabb bemenetet és kimenetet kapunk a hálózat képzéséhez, és jobban viselkedik, mint a felügyelt képzés.

A tapasztalatok visszajátszásával a legnagyobb teljesítményjavulás a DQN-ben. A célhálózat javulása jelentős, de nem olyan kritikus, mint a visszajátszás. De fontosabbá válik, ha a hálózat kapacitása kicsi.

Mély Q-tanulás tapasztalati visszajátszással

Itt az algoritmus:

ahol ϕ előfeldolgozza az utolsó 4 képkockát az állapot ábrázolásához. A mozgás rögzítéséhez négy képkockát használunk egy állapot reprezentálására.

Implementációs részletek

Veszteségfüggvény

Nézzünk át még néhány implementációs részletet a teljesítmény javítása érdekében. A DQN Huber-veszteséget használ (zöld görbe), ahol a veszteség kis a értékek esetén kvadratikus, nagy értékek esetén pedig lineáris.

A Huber-veszteség bevezetése kevésbé drámai változásokat tesz lehetővé, amelyek gyakran ártanak az RL-nek.

Optimalizálás

Az RL képzés érzékeny az optimalizálási módszerekre. Az egyszerű tanulási sebesség ütemezése nem elég dinamikus ahhoz, hogy kezelni tudja a bemenet változását a képzés során. Sok RL képzés RMSProp vagy Adam optimalizálót használ. A DQN-t RMSProp segítségével képzik. A Policy Gradient módszereknél az előzetes optimalizálási módszer használata szintén erősen tanulmányozott.

ϵ-greedy

A DQN ϵ-greedy-t használ az első akció kiválasztására.

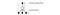
A képzés javítása érdekében a ϵ 1-ről indul és 0-ra lágyul.1 vagy 0,05 az első egymillió képkocka alatt a következő szabályzattal.

ahol m a lehetséges cselekvések száma. A képzés elején egyenletesen választjuk ki a lehetséges akciókat, de a képzés előrehaladtával egyre gyakrabban választjuk ki az optimális a* akciót. Ez lehetővé teszi a maximális felfedezést az elején, amely végül kihasználásra vált.

De még a tesztelés során is fenntarthatjuk ϵ egy kis értéket, például 0,05-öt. A determinisztikus politika megrekedhet egy lokális optimumban. Egy nemdeterminisztikus politika lehetővé teszi számunkra, hogy kitörjünk egy jobb optimum elérésének esélyéért.

Architektúra

Itt a DQN architektúra. Az utolsó 4 előző videóképet vesszük és betápláljuk a konvolúciós rétegekbe, majd a teljesen összekapcsolt rétegekbe, hogy kiszámítsuk a Q értékeket minden egyes akcióhoz.

Az alábbi példában, ha nem mozdítjuk felfelé az ütőt a 3. képkockán, akkor elhibázzuk a labdát. Ahogy a DQN alapján várható volt, az evező felfelé mozgatásának Q értéke sokkal magasabb a többi akcióhoz képest.

A DQN javításai

A DQN-ben számos javítás történt. Ebben a részben bemutatunk néhány módszert, amelyek jelentős fejlesztéseket mutatnak be.

Dupla DQN

A Q-tanulásban a következő képletet használjuk a Q célértékére.

A max művelet azonban pozitív torzítást eredményez a Q becslések felé.

A fenti példából látható, hogy a max Q(s, a) nagyobb, mint a konvergens 1 érték.0. azaz a max művelet túlbecsüli a Q-t. Az elmélet és a kísérletek alapján a DQN teljesítménye javul, ha a θ online hálózatot használjuk a művelet mohó kiválasztására és a θ- célhálózatot a Q érték becslésére.

Prioritized Experience Replay

DQN az átmeneteket a visszajátszási pufferből egyenletesen veszi ki. Kevesebb figyelmet kell azonban fordítanunk azokra a mintákra, amelyek már közel vannak a célhoz. Azokat az átmeneteket kell mintavételeznünk, amelyeknek nagy a céltávolsága:

Ezért a pufferből

• a fenti hibaérték alapján választhatunk átmeneteket (a nagyobb hibával rendelkező átmeneteket gyakrabban választjuk ki), vagy
• a hibaérték alapján rangsoroljuk őket, és a rangsor szerint választjuk ki (a magasabb rangúakat gyakrabban választjuk ki).

A mintavételi adatokra vonatkozó egyenletek részleteit lásd a Prioritized Experience Replay című dokumentumban.

Dueling DQN

A Dueling DQN-ben a Q-t az alábbiakban egy másik képlettel számítjuk ki V értékfüggvénnyel és egy állapotfüggő A akcióelőny-függvénnyel:

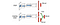
A Q megtanulása helyett két külön fejet használunk V és A kiszámítására. Empirikus kísérletek azt mutatják, hogy a teljesítmény javul. A DQN csak egy adott akcióhoz frissíti az állapot Q-értékfüggvényét. A párbajozó DQN frissíti V-t, amit más Q(s, a’) frissítések is kihasználhatnak. Így minden egyes Dueling DQN képzési iterációról azt gondoljuk, hogy nagyobb hatással van.

Noisy Nets for Exploration

A DQN ϵ-greedy-t használ az akciók kiválasztására. Alternatívaként a NoisyNet úgy helyettesíti azt, hogy a lineáris réteghez parametrikus zajt ad a felfedezés segítésére. A NoisyNet-ben az ε-greedy nem használatos. Egy mohó módszert használ a Q-érték függvényből történő akciók kiválasztására. A Q approximátor teljesen összekapcsolt rétegeihez azonban a cselekvések felfedezéséhez képezhető paraméteres zajt adunk az alábbiakban. A zaj hozzáadása egy mély hálózathoz gyakran egyenértékű vagy jobb, mint a ϵ-greedy módszerhez hasonló zaj hozzáadása egy akcióhoz.

Még több gondolat

A DQN az RL egyik fontos osztályába, az értéktanulásba tartozik. A gyakorlatban a valós problémák megoldása során gyakran kombináljuk a politika gradienseket az értéktanulási módszerekkel.