Beszűkített Boltzmann-gépek – egyszerűsítve
Mi a korlátozott Boltzmann-gépek?
Az RBM-ek egy kétrétegű mesterséges neurális hálózat generatív képességekkel. Képesek megtanulni egy valószínűségi eloszlást a bemeneti halmazon. Az RBM-eket Geoffrey Hinton találta fel, és dimenziócsökkentésre, osztályozásra, regresszióra, kollaboratív szűrésre, jellemzőtanulásra és témamodellezésre használhatók.
Az RBM-ek a Boltzmann-gépek egy speciális osztálya, és a látható és a rejtett egységek közötti kapcsolatok tekintetében korlátozottak. Ez megkönnyíti a megvalósításukat a Boltzmann-gépekhez képest. Mint korábban említettük, kétrétegű neurális hálózatról van szó (az egyik a látható réteg, a másik a rejtett réteg), és ez a két réteg egy teljesen kétosztatú gráffal van összekötve. Ez azt jelenti, hogy a látható réteg minden csomópontja kapcsolódik a rejtett réteg minden csomópontjához, de két azonos csoportba tartozó csomópont nem kapcsolódik egymáshoz. Ez a korlátozás hatékonyabb képzési algoritmusokat tesz lehetővé, mint ami a Boltzmann-gépek általános osztályára rendelkezésre áll, különösen a gradiens alapú kontrasztív divergencia algoritmust.
Egy korlátozott Boltzmann-gép így néz ki:
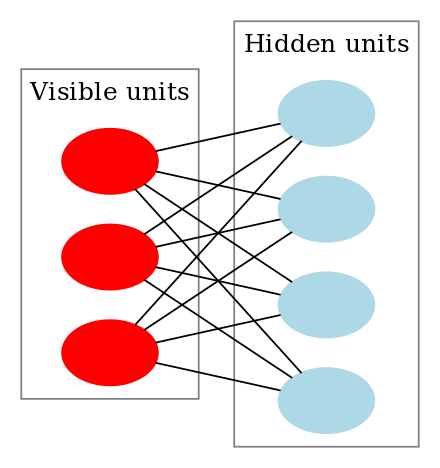
Hogyan működnek a korlátozott Boltzmann-gépek?
Egy RBM-ben egy szimmetrikus kétrészes gráffal rendelkezünk, ahol nincs két olyan egység, amely ugyanazon csoporton belül összekapcsolódik. Több RBM is lehet stacked és finomhangolható a gradiens süllyedés és a back-propagáció folyamatával. Az ilyen hálózatot Deep Belief Networknek nevezzük. Bár az RBM-eket alkalmanként használják, a legtöbb ember a mélytanulási közösségben elkezdte felváltani a használatukat az általános adverzális hálózatokkal vagy a variációs autókódolókkal.
A RBM egy sztochasztikus neurális hálózat, ami azt jelenti, hogy minden neuron valamilyen véletlenszerű viselkedést mutat aktiváláskor. Az RBM-ben két további torzító egységréteg van (rejtett torzítás és látható torzítás). Ez különbözteti meg az RBM-et az autoencodertől. A rejtett előfeszítésű RBM az aktiválást az előremenő átmeneten állítja elő, a látható előfeszítés pedig segít az RBM-nek a bemenet rekonstruálásában a visszafelé történő átmenet során. A rekonstruált bemenet mindig különbözik a tényleges bemenettől, mivel a látható egységek között nincsenek kapcsolatok, és ezért nem tudnak információt átadni egymás között.

A fenti kép a több bemenettel rendelkező RBM képzésének első lépését mutatja. A bemeneteket megszorozzuk a súlyokkal, majd hozzáadjuk az előfeszítést. Az eredményt ezután egy szigmoid aktiválási függvényen vezetjük át, és a kimenet határozza meg, hogy a rejtett állapot aktiválódik-e vagy sem. A súlyok egy mátrix lesznek, amelyben a bemeneti csomópontok száma a sorok száma, a rejtett csomópontok száma pedig az oszlopok száma. Az első rejtett csomópont a bemeneteknek a súlyok első oszlopával megszorzott vektorszorzatát kapja, mielőtt a megfelelő előfeszítési kifejezés hozzáadódik.
És ha kíváncsi vagy, mi az a szigmoid függvény, íme a képlet:

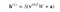
ahol h(1) és v(0) a rejtett és a látható réteg megfelelő vektorai (oszlopmátrixai), a felirat az iterációt jelenti (v(0) a bemenetet jelenti, amit a hálózatnak adunk), a pedig a rejtett réteg előfeszítési vektora.
(Megjegyezzük, hogy itt vektorokról és mátrixokról van szó, nem pedig egydimenziós értékekről.)

Ez a kép most a fordított fázist vagy a rekonstrukciós fázist mutatja. Hasonló az első menethez, de ellentétes irányban. Az egyenlet így jön ki:
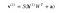
Leave a Reply