Machines de Boltzmann restreintes – Simplifiées
Qu’est-ce que les machines de Boltzmann restreintes ?
Les RBM sont un réseau neuronal artificiel à deux couches doté de capacités génératives. Elles ont la capacité d’apprendre une distribution de probabilité sur son ensemble d’entrée. Les RBM ont été inventés par Geoffrey Hinton et peuvent être utilisés pour la réduction de la dimensionnalité, la classification, la régression, le filtrage collaboratif, l’apprentissage de caractéristiques et la modélisation de sujets.
Les RBM sont une classe spéciale de machines de Boltzmann et ils sont restreints en termes de connexions entre les unités visibles et cachées. Cela facilite leur mise en œuvre par rapport aux machines de Boltzmann. Comme indiqué précédemment, il s’agit d’un réseau neuronal à deux couches (l’une étant la couche visible et l’autre la couche cachée) et ces deux couches sont connectées par un graphe entièrement biparti. Cela signifie que chaque nœud de la couche visible est connecté à chaque nœud de la couche cachée, mais que deux nœuds du même groupe ne sont pas connectés l’un à l’autre. Cette restriction permet des algorithmes d’apprentissage plus efficaces que ce qui est disponible pour la classe générale des machines de Boltzmann, en particulier, l’algorithme de divergence contrastive basé sur le gradient.
Une machine de Boltzmann restreinte ressemble à ceci :
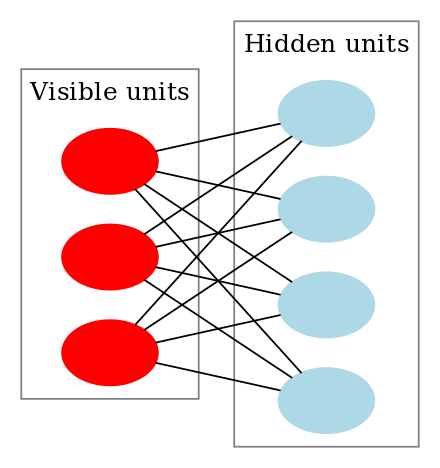
Comment fonctionnent les machines de Boltzmann restreintes ?
Dans une RBM, nous avons un graphe biparti symétrique où aucune unité du même groupe n’est connectée. Plusieurs RBM peuvent également être stackedet peuvent être affinés par le processus de descente de gradient et de rétropropagation. Un tel réseau est appelé réseau de croyance profond. Bien que les RBM soient occasionnellement utilisés, la plupart des personnes de la communauté de l’apprentissage profond ont commencé à remplacer leur utilisation par des réseaux adversariens généraux ou des autoencodeurs variationnels.
Le RBM est un réseau neuronal stochastique, ce qui signifie que chaque neurone aura un certain comportement aléatoire lorsqu’il sera activé. Il y a deux autres couches d’unités de biais (biais caché et biais visible) dans un RBM. C’est ce qui rend les RBM différents des autoencodeurs. Le biais caché du RBM produit l’activation lors du passage en avant et le biais visible aide le RBM à reconstruire l’entrée lors d’un passage en arrière. L’entrée reconstruite est toujours différente de l’entrée réelle car il n’y a pas de connexions entre les unités visibles et donc, aucun moyen de transférer des informations entre elles.

L’image ci-dessus montre la première étape de la formation d’un RBM avec plusieurs entrées. Les entrées sont multipliées par les poids, puis ajoutées au biais. Le résultat est ensuite passé par une fonction d’activation sigmoïde et la sortie détermine si l’état caché est activé ou non. Les poids seront une matrice avec le nombre de nœuds d’entrée comme nombre de lignes et le nombre de nœuds cachés comme nombre de colonnes. Le premier nœud caché recevra la multiplication vectorielle des entrées multipliées par la première colonne de poids avant que le terme de biais correspondant ne lui soit ajouté.
Et si vous vous demandez ce qu’est une fonction sigmoïde, voici la formule :

Donc l’équation que nous obtenons dans cette étape serait,
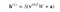
où h(1) et v(0) sont les vecteurs correspondants (matrices colonnes) pour les couches cachées et visibles avec l’exposant comme itération (v(0) signifie l’entrée que nous fournissons au réseau) et a est le vecteur de biais de la couche cachée.
(Notez que nous traitons ici des vecteurs et des matrices et non des valeurs unidimensionnelles.)

Maintenant cette image montre la phase inverse ou la phase de reconstruction. Elle est similaire à la première passe mais dans la direction opposée. L’équation s’avère être :
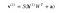
.
Leave a Reply