El cuarteto de Anscombe

19 de septiembre, 2018 – 2 min read

Siempre he creído en aquello de «los cálculos numéricos son exactos, pero las gráficas son aproximadas». Viniendo de una persona que acaba de empezar a aprender Data Analytics, era difícil para mí entender la importancia de la Visualización de Datos junto con las estadísticas de resumen. Pero todo cambió después de asistir a este Meetup de Visualización de Datos, que es cuando me presentaron el Cuarteto de Anscombe.

El Cuarteto de Anscombe fue desarrollado por el estadístico Francis Anscombe. Comprende cuatro conjuntos de datos, cada uno de los cuales contiene once pares (x,y). Lo esencial de estos conjuntos de datos es que comparten los mismos estadísticos descriptivos. Pero las cosas cambian completamente, y debo subrayar COMPLETAMENTE, cuando se grafican. Cada gráfico cuenta una historia diferente, independientemente de que sus estadísticas de resumen sean similares.

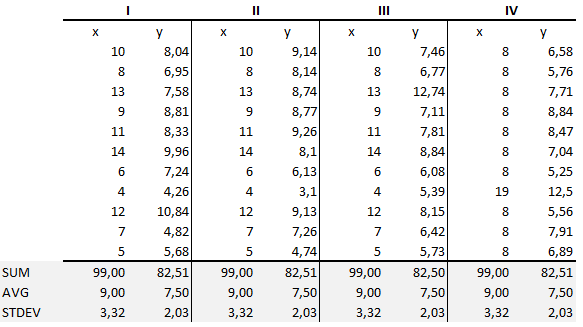
Las estadísticas de resumen muestran que las medias y las varianzas eran idénticas para x e y en todos los grupos :

• La media de x es 9 y la de y es 7.50 para cada conjunto de datos.
• De igual manera, la varianza de x es 11 y la varianza de y es 4,13 para cada conjunto de datos
• El coeficiente de correlación (cuán fuerte es la relación entre dos variables) entre x e y es 0.816 para cada conjunto de datos

Cuando trazamos estos cuatro conjuntos de datos en un plano de coordenadas x/y, podemos observar que muestran las mismas líneas de regresión también pero cada conjunto de datos está contando una historia diferente :

• El conjunto de datos I parece tener modelos lineales limpios y bien ajustados.
• El conjunto de datos II no se distribuye con normalidad.
• En el conjunto de datos III la distribución es lineal, pero la regresión calculada está desviada por un valor atípico.
• El conjunto de datos IV muestra que un valor atípico es suficiente para producir un alto coeficiente de correlación.

Este cuarteto destaca la importancia de la visualización en el análisis de datos. La observación de los datos revela gran parte de la estructura y una imagen clara del conjunto de datos.

Un ordenador debe realizar tanto cálculos como gráficos. Ambos tipos de resultados deben ser estudiados; cada uno contribuirá a la comprensión.