Omezené Boltzmannovy stroje – zjednodušeně
Co jsou to omezené Boltzmannovy stroje?
RBM jsou dvouvrstvé umělé neuronové sítě s generativními schopnostmi. Mají schopnost naučit se pravděpodobnostní rozdělení nad svou množinou vstupů. RBM vynalezl Geoffrey Hinton a lze je použít pro redukci dimenzionality, klasifikaci, regresi, kolaborativní filtrování, učení příznaků a modelování témat.
RBM jsou speciální třídou Boltzmannových strojů a jsou omezeny z hlediska spojení mezi viditelnými a skrytými jednotkami. To usnadňuje jejich implementaci ve srovnání s Boltzmannovými stroji. Jak již bylo uvedeno, jsou to dvouvrstvé neuronové sítě (jedna je viditelná vrstva a druhá skrytá vrstva) a tyto dvě vrstvy jsou propojeny plně bipartitním grafem. To znamená, že každý uzel ve viditelné vrstvě je propojen s každým uzlem ve skryté vrstvě, ale žádné dva uzly ve stejné skupině nejsou propojeny navzájem. Toto omezení umožňuje použít efektivnější tréninkové algoritmy, než jaké jsou k dispozici pro obecnou třídu Boltzmannových strojů, zejména algoritmus kontrastní divergence založený na gradientu.
Omezený Boltzmannův stroj vypadá takto:
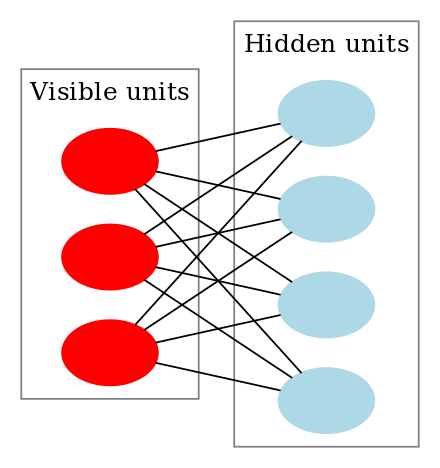
Jak fungují omezené Boltzmannovy stroje?
V RBM máme symetrický bipartitní graf, kde žádné dvě jednotky ve stejné skupině nejsou propojeny. Více RBM může být také stackeda lze je jemně doladit pomocí procesu gradientního sestupu a zpětného šíření. Taková síť se nazývá Deep Belief Network. Přestože se RBM občas používají, většina lidí v komunitě hlubokého učení začala jejich používání nahrazovat obecnými adverzními sítěmi nebo variačními autoenkodéry.
RBM je stochastická neuronová síť, což znamená, že každý neuron bude mít při aktivaci určité náhodné chování. V RBM existují další dvě vrstvy zkreslujících jednotek (skryté zkreslení a viditelné zkreslení). Tím se RBM liší od autoenkodérů. Skryté zkreslení RBM vytváří aktivaci při dopředném průchodu a viditelné zkreslení pomáhá RBM rekonstruovat vstup při zpětném průchodu. Rekonstruovaný vstup se vždy liší od skutečného vstupu, protože mezi viditelnými jednotkami neexistují žádná spojení, a proto si mezi sebou nemohou předávat informace.

Výše uvedený obrázek ukazuje první krok při trénování RBM s více vstupy. Vstupy se vynásobí váhami a poté se přičtou ke zkreslení. Výsledek pak projde sigmoidní aktivační funkcí a výstup určí, zda se skrytý stav aktivuje, nebo ne. Váhy budou matice s počtem vstupních uzlů jako počtem řádků a počtem skrytých uzlů jako počtem sloupců. První skrytý uzel obdrží vektorový násobek vstupů vynásobený prvním sloupcem vah, než se k němu přičte příslušný člen zkreslení.
A pokud vás zajímá, co je to sigmoidní funkce, zde je vzorec:

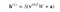
kde h(1) a v(0) jsou odpovídající vektory (sloupcové matice) pro skrytou a viditelnou vrstvu s horním indexem jako iterací (v(0) znamená vstup, který poskytujeme síti) a a je vektor zkreslení skryté vrstvy.
(Všimněte si, že zde máme co do činění s vektory a maticemi, nikoli s jednorozměrnými hodnotami)

Nyní tento obrázek ukazuje zpětnou fázi neboli fázi rekonstrukce. Je podobná prvnímu průchodu, ale v opačném směru. Rovnice vychází takto:
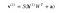
.
Leave a Reply