Anscombovo kvarteto

19. září, 2018 – 2 minuty čtení

Vždycky jsem věřil, že „numerické výpočty jsou přesné, ale grafy jsou hrubé“. Vzhledem k tomu, že pocházím z člověka, který se právě začal učit analýzu dat, bylo pro mě těžké pochopit význam vizualizace dat spolu se souhrnnou statistikou. Ale vše se změnilo po účasti na tomto Data Visualization Meetup, kdy jsem se seznámil s Anscombovým kvartetem.

Anscombův kvartet vyvinul statistik Francis Anscombe. Skládá se ze čtyř datových sad, z nichž každá obsahuje jedenáct dvojic (x,y). Podstatné u těchto datových sad je, že mají stejnou popisnou statistiku. Věci se však zcela změní, a musím zdůraznit ÚPLNĚ, když se zobrazí v grafech. Každý graf vypovídá o něčem jiném bez ohledu na jejich podobné souhrnné statistiky.

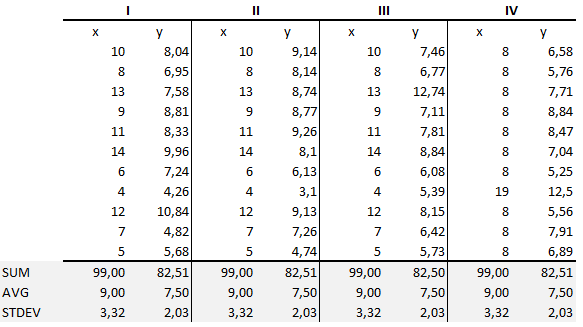
Souhrnné statistiky ukazují, že průměry a rozptyly byly pro x a y ve všech skupinách stejné :

• Prostřední hodnota x je 9 a průměrná hodnota y je 7. To znamená, že každý graf vypovídá o něčem jiném.50 pro každý soubor dat.
• Podobně rozptyl x je 11 a rozptyl y je 4,13 pro každý soubor dat
• Koeficient korelace (jak silný je vztah mezi dvěma proměnnými) mezi x a y je 0 %.816 pro každý soubor dat

Když tyto čtyři soubory dat vyneseme do souřadnicové roviny x/y, můžeme pozorovat, že ukazují i stejné regresní přímky, ale každý soubor dat vypovídá o něčem jiném :

• Datový soubor I se zdá mít čisté a dobře padnoucí lineární modely.
• Datová sada II nemá normální rozdělení.
• V datové sadě III je rozdělení lineární, ale vypočtenou regresi shazuje odlehlá hodnota.
• Datová sada IV ukazuje, že k vytvoření vysokého korelačního koeficientu stačí jedna odlehlá hodnota.

Toto kvarteto zdůrazňuje význam vizualizace při analýze dat. Pohled na data odhalí velkou část struktury a jasný obraz datové sady.

Počítač by měl provádět výpočty i grafy. Oba druhy výstupů by se měly studovat; každý z nich přispěje k pochopení.