Was ist analytische Geometrie?
Was ist analytische Geometrie?
Die analytische Geometrie ist ein Zweig der Algebra, der zur Modellierung geometrischer Objekte verwendet wird – Punkte, (gerade) Linien und Kreise sind die grundlegendsten davon. Die analytische Geometrie ist eine großartige Erfindung von Descartes und Fermat.
In der ebenen analytischen Geometrie sind Punkte als geordnete Zahlenpaare definiert, z.B. (x, y), während die Geraden wiederum als Punktmengen definiert sind, die lineare Gleichungen erfüllen, siehe die ausgezeichneten Darstellungen von D. Pedoe oder D. Brannan et al. Aus der Sicht der analytischen Geometrie sind geometrische Axiome ableitbare Theoreme. Zum Beispiel gibt es für zwei beliebige Punkte (x1, y1) und (x2, y2) eine einzige Linie ax + by + c = 0, die durch diese Punkte verläuft. Ihre Koeffizienten a, b, c lassen sich (bis auf einen konstanten Faktor) aus dem linearen System zweier Gleichungen
| ax1 + by1 + c = 0 ax2 + by2 + c = 0 finden, |
oder direkt aus der Determinantengleichung
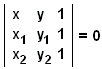 |
Allerdings kann keine axiomatische Theorie auf unbestimmte Elemente verzichten. In der Mengenlehre, die einem Großteil der Mathematik und insbesondere der analytischen Geometrie zugrunde liegt, bleibt der grundlegendste Begriff der Menge undefiniert.
Die Geometrie des dreidimensionalen Raums wird mit Dreiergruppen von Zahlen (x, y, z) modelliert und eine 3D-Lineargleichung ax + by + cz + d = 0 definiert eine Ebene. Im Allgemeinen bietet die analytische Geometrie ein bequemes Werkzeug für die Arbeit in höheren Dimensionen.
Im Rahmen der analytischen Geometrie kann man auch nicht-euklidische Geometrien modellieren (und tut dies auch). Zum Beispiel ist in der ebenen projektiven Geometrie ein Punkt ein Tripel von homogenen Koordinaten (x, y, z), die nicht alle 0 sind, so dass
| (tx, ty, tz) = (x, y, z), |
für alle t ≠ 0, während eine Gerade durch eine homogene Gleichung
| ax + bx + cz = 0 beschrieben wird. |
In der analytischen Geometrie werden Kegelschnitte durch Gleichungen zweiten Grades definiert:
| ax² + bxy + cy² + dx + ey + f = 0. |
Der Teil der analytischen Geometrie, der sich hauptsächlich mit linearen Gleichungen beschäftigt, heißt Lineare Algebra.
Die kartesische analytische Geometrie ist eine Geometrie, in der die Achsen x = 0 und y = 0 senkrecht aufeinander stehen.
Die Komponenten des n-Tupels x = (x1, …, xn) werden als seine Koordinaten bezeichnet. Wenn n = 2 oder n = 3, wird die erste Koordinate Abszisse und die zweite Ordinate genannt.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Kontakt||Titelseite||Inhalt||Geometrie||oben|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply