Teil 14 : Punkt- und Hadamard-Produkt

Neben der bereits besprochenen Matrixmultiplikation können Vektoren durch zwei weitere Methoden multipliziert werden: Punktprodukt und Hadamard-Produkt. Die Ergebnisse beider Methoden sind unterschiedlich.

Die Elemente, die der gleichen Zeile und Spalte entsprechen, werden miteinander multipliziert und die Produkte werden addiert, so dass das Ergebnis ein Skalar ist.

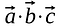
Im Gegensatz zur Matrixmultiplikation ist das Ergebnis des Punktprodukts kein weiterer Vektor oder eine Matrix, sondern ein Skalar.

Die Reihenfolge der Vektoren spielt beim Punktprodukt keine Rolle, nur die Anzahl der Elemente in beiden Vektoren sollte gleich sein.

Die geometrische Formel für das Punktprodukt lautet

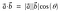
Das Punktprodukt wird auch inneres Produkt oder Skalarprodukt genannt.

Projektion eines Vektors

Angenommen, wir haben zwei Vektoren c und d, die unter dem Winkel phi(Ф) stehen.

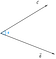
Nun, kann die Projektion des Vektors c auf den Vektor d wie folgt dargestellt werden

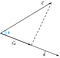
Wir können aus der Abbildung schließen, dass die Projektion gleich der horizontalen Komponente des Vektors c in Bezug auf den Winkel phi(Ф) ist.

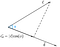
Dies nennt man skalare Projektion.Um die Vektorprojektion des Vektors c auf den Vektor d zu finden, müssen wir die Skalarprojektion mit dem Einheitsvektor d multiplizieren.

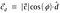
Substitutionswert des Einheitsvektors d.

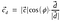
Damit, Punktprodukt auch als

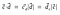
Projektionen finden in der linearen Algebra und im maschinellen Lernen breite Anwendung (Support Vector Machine(SVM) ist ein maschineller Lernalgorithmus, der zur Klassifizierung von Daten verwendet wird).

Hadamard-Produkt (elementweise Multiplikation)

Das Hadamard-Produkt zweier Vektoren ist der Matrixaddition sehr ähnlich: Elemente, die den gleichen Zeilen und Spalten gegebener Vektoren/Matrizen entsprechen, werden miteinander multipliziert, um einen neuen Vektor/Matrix zu bilden.

Benannt nach dem französischen Mathematiker Jacques Hadamard.

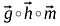
Die Reihenfolge der zu multiplizierenden Matrizen/Vektoren sollte gleich sein und die resultierende Matrix wird auch die gleiche Reihenfolge haben.

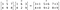
Das Hadamard-Produkt wird in Bildkomprimierungsverfahren wie JPEG verwendet. Es ist auch als Schur-Produkt bekannt, nach dem deutschen Mathematiker Issai Schur.

Das Hadamard-Produkt wird in LSTM-Zellen (Long Short-Term Memory) von rekurrenten neuronalen Netzen (RNNs) verwendet.