Vad är analytisk geometri?
Vad är analytisk geometri?
Analytisk geometri är en gren av algebra som används för att modellera geometriska objekt – punkter, (raka) linjer och cirklar är de mest grundläggande av dessa. Analytisk geometri är en stor uppfinning av Descartes och Fermat.
I plan analytisk geometri definieras punkter som ordnade talpar, till exempel (x, y), medan de raka linjerna i sin tur definieras som uppsättningar av punkter som uppfyller linjära ekvationer, se de utmärkta utläggningarna av D. Pedoe eller D. Brannan m.fl. Ur den analytiska geometrins synvinkel är geometriska axiom härledbara satser. Till exempel finns det för två olika punkter (x1, y1) och (x2, y2) en enda linje ax + by + c = 0 som går genom dessa punkter. Dess koefficienter a, b, c kan hittas (upp till en konstant faktor) från det linjära systemet av två ekvationer
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
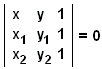 |
Ingen axiomatisk teori kan dock undgå att använda odefinierade element. I mängdteorin som ligger till grund för en stor del av matematiken och i synnerhet den analytiska geometrin förblir det mest grundläggande begreppet mängd odefinierat.
Geometrin i det tredimensionella rummet modelleras med triplar av tal (x, y, z) och en 3D-linjär ekvation ax + by + cz + d = 0 definierar ett plan. I allmänhet ger analytisk geometri ett bekvämt verktyg för att arbeta i högre dimensioner.
Inom ramen för analytisk geometri kan man (och gör) också modellera icke-euklidiska geometrier. I plan projektiv geometri är till exempel en punkt en trippel av homogena koordinater (x, y, z), inte alla 0, så att
| (tx, ty, tz) = (x, y, z), |
för alla t ≠ 0, medan en linje beskrivs av en homogen ekvation
| ax + bx + cz = 0. |
| ax² + bxy + cy² + dx + ey + f = 0. |
Den del av den analytiska geometrin som huvudsakligen behandlar linjära ekvationer kallas linjär algebra.
Kartesiansk analytisk geometri är geometri där axlarna x = 0 och y = 0 är vinkelräta.
Komponenterna i n-tupeln x = (x1, …, xn) kallas dess koordinater. När n = 2 eller n = 3 kallas den första koordinaten för abscissa och den andra för ordinata.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Kontakt||Framsidan||Innehåll||Geometri||upp|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply