Articles /

Matematik för de fria konsterna

Lärandemål

  • Definiera och identifiera självlikhet i geometriska former, växter, och geologiska formationer
  • Generera en fraktalform med hjälp av en initiator och en generator
  • Skalera ett geometriskt objekt med en specifik skalfaktor med hjälp av relationen mellan skaldimensionen
  • Bestäm den fraktala dimensionen hos ett fraktalt objekt

Fraktaler uppvisar, förutom visuell självlikhet, även andra intressanta egenskaper. Lägg till exempel märke till att varje steg i Sierpinski-packningens iteration tar bort en fjärdedel av den återstående ytan. Om denna process fortsätter i all oändlighet skulle det sluta med att vi i princip tar bort all yta, vilket innebär att vi började med en tvådimensionell yta och på något sätt slutar med något mindre än så, men till synes mer än bara en endimensionell linje.

För att utforska denna idé måste vi diskutera dimension. Något som en linje är 1-dimensionellt; den har bara längd. Varje kurva är 1-dimensionell. Saker som lådor och cirklar är 2-dimensionella, eftersom de har längd och bredd, vilket beskriver en yta. Föremål som lådor och cylindrar har längd, bredd och höjd, vilket beskriver en volym, och är 3-dimensionella.

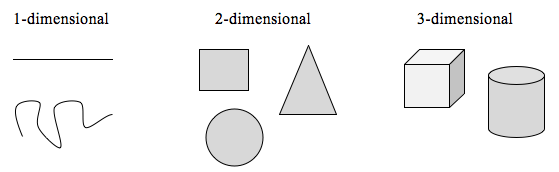
1-dimensionella föremål är till exempel en rak linje och en oregelbunden vågig linje. Tvådimensionella objekt inkluderar en rektangel, en triangel och en cirkel. Tredimensionella objekt inkluderar en kub och en cylinder.

Vissa regler gäller för skalning av objekt, relaterade till deras dimension.

Om jag hade en linje med längden 1, och ville skala dess längd med 2, skulle jag behöva två kopior av den ursprungliga linjen. Om jag hade en linje med längden 1, och ville skala dess längd med 3, skulle jag behöva tre kopior av originalet.

1, en horisontell linje. 2, en horisontell linje som är dubbelt så lång. 3, en horisontell linje som är tre gånger så lång.

Om jag hade en rektangel med längden 2 och höjden 1, och ville skala dess längd och bredd med 2, skulle jag behöva fyra kopior av den ursprungliga rektangeln. Om jag ville skala längden och bredden med 3 skulle jag behöva nio kopior av den ursprungliga rektangeln.

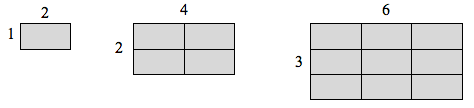
En rektangel med sidorna som mäter 1 och 2. Därefter fyra kopior av den rektangeln för att bilda en större rektangel med sidorna 2 och 4. Därefter nio kopior av den första rektangeln för att bilda en större rektangel med sidorna med måtten 3 och 6.

Om jag hade en kubisk låda med sidorna med längden 1, och ville skala dess längd och bredd med 2, skulle jag behöva åtta kopior av den ursprungliga kuben. Om jag vill skala längden och bredden med 3 skulle jag behöva 27 kopior av den ursprungliga kuben.

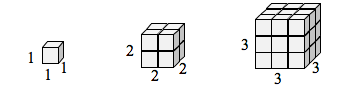
En kub med sidorna som mäter 1 gånger 1 gånger 1 gånger 1. Därefter åtta kopior av den kuben för att bilda en större kub med sidorna som mäter 2 gånger 2 gånger 2 gånger 2. Därefter 27 kopior av den ursprungliga kuben för att bilda en större kub som mäter 3 gånger 3 gånger 3 gånger 3.

Bemärk att i det 1-dimensionella fallet är nödvändiga kopior = skala.

I det 2-dimensionella fallet är nödvändiga kopior = skala^{2}.

I det 3-dimensionella fallet är nödvändiga kopior = skala^{3}.

Utifrån dessa exempel kan vi dra ett mönster.

Skalering-Dimension-relation

För att skala en D-dimensionell form med en skalningsfaktor S, kommer antalet kopior C av den ursprungliga formen som behövs att ges av:

\text{Kopior}=\text{Skalering}^{\text{Dimension}}, eller C=S^{D}

Exempel

Använd skalnings- och dimensionsrelationen för att bestämma dimensionen för Sierpinski-packningen.

Antag att vi definierar den ursprungliga packningen till att ha sidlängden 1. Den större packningen som visas är dubbelt så bred och dubbelt så hög, så den har skalats med en faktor 2.

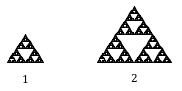
Sierpinski packningstriangel. Därefter en större triangel som består av tre Sierpinski-packningstrianglar och en vit triangel i mitten.

Bemärk att för att konstruera den större packningen behövs tre kopior av den ursprungliga packningen.

Med hjälp av skalnings- och dimensionsrelationen C=S^{D} får vi ekvationen 3=2^{D}.

Med tanke på att 2^{1}=2 och 2^{2}=4 kan vi omedelbart se att D ligger någonstans mellan 1 och 2. Packningen är mer än en 1-dimensionell form, men vi har tagit bort så mycket yta att den nu är mindre än 2-dimensionell.

För att lösa ekvationen 3=2^{D} krävs logaritmer. Om du har studerat logaritmer tidigare kommer du kanske ihåg hur du löser den här ekvationen (om inte, hoppa bara till rutan nedan och använd den formeln med log-tangenten på en miniräknare):

Ta logaritmen av båda sidorna.

3={{{2}^{D}}}

Använd logaritmernas exponentegenskap.

\log(3)=\log\vänster({{2}^{D}}\höger)

Divider med log(2).

\log(3)=D\log\left(2\right)

Dimensionen på packningen är ungefär 1,585.

D=\frac{\log\left(3\right)}{\log(2)}\avsnitt 1.585

Skalering-Dimension Relation, för att hitta Dimension

För att hitta dimensionen D hos en fraktal, bestäm skalningsfaktorn S och det antal kopior C av den ursprungliga formen som behövs, använd sedan formeln

D=\frac{\log\ vänster(C\höger)}{\log(S)}

Try It

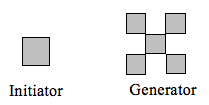
Bestäm fraktaldimensionen för den fraktal som produceras med hjälp av initiatorn och generatorn.

Initiatorn är en kvadrat. Generatorn är fem kvadrater som bildar ett rutmönster.
Visa lösningen

Skalering av fraktalen med en faktor 3 kräver 5 kopior av originalet.

D=\frac{\text{log}\left(5\right)}{\text{log}\left(3\right)}\approx1.465

I följande video presenterar vi ett fungerande exempel på hur man bestämmer dimensionen av Sierpinski-packningen

.

Leave a Reply