Introduktion till dekonvolution

Dekonvolution är en beräkningsintensiv bildbehandlingsteknik som i allt högre grad används för att förbättra kontrasten och upplösningen hos digitala bilder som tas i mikroskop. Grunden bygger på en uppsättning metoder som är utformade för att ta bort eller vända den oskärpa som finns i mikroskopbilder och som induceras av objektivets begränsade öppning.

Nästan alla bilder som förvärvats i ett digitalt fluorescensmikroskop kan dekonvolutioneras, och flera nya tillämpningar håller på att utvecklas som tillämpar tekniker för dekonvolutionering av bilder av genomlyst ljus som samlats in under en mängd olika kontrastförbättrande strategier. Bland de mest lämpliga ämnena för förbättring genom dekonvolution är tredimensionella montage som konstrueras av en serie optiska sektioner.

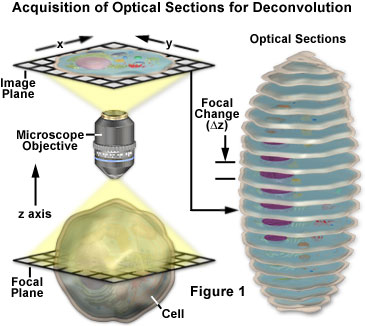
De grundläggande koncepten kring förvärv av z-serier av bilder för dekonvolutionsanalys presenteras med ett schematiskt diagram i figur 1. En serie bilder registreras av provet, var och en förskjuten något från varandra längs z-axeln. Denna förändring av fokalplanet resulterar i en något annorlunda bild, med subtila förändringar som orsakas av ofokuserat ljus som kommer ovanför och under det aktuella z-planet. Under avvecklingsanalysen analyseras hela z-serien för att skapa en tydligare, mer högupplöst datauppsättning som inte är snedvriden av fluorescens utanför fokus.

Dekonvolution föreslås ofta som ett bra alternativ till det konfokala mikroskopet, eftersom båda teknikerna försöker att minimera effekten av fluorescens utanför fokus på din slutliga bild. Detta är inte strikt sant eftersom bilder som förvärvats med hjälp av en pinhole-öppning i ett konfokalmikroskop gynnas av behandling av dekonvolution. Vid konfokalmikroskopi förhindrar man att ljus som inte är fokuserat upptäcks genom att placera en hålöppning mellan objektivet och detektorn, genom vilken endast ljusstrålar som är fokuserade kan passera. Däremot tillåter widefield-mikroskop att ljus utanför fokus passerar direkt till detektorn. Dekonvolution tillämpas sedan på de resulterande bilderna för att antingen subtrahera det ofokuserade ljuset eller återföra det till sin källa. Konfokal mikroskopi lämpar sig särskilt väl för att undersöka tjocka exemplar, t.ex. embryon eller tussar, medan widefield-deconvolution har visat sig vara ett kraftfullt verktyg för att avbilda exemplar som kräver extremt låga ljusnivåer. Dessa verktyg kan till och med kombineras för att minska bruset i bilder som förvärvats med ett konfokalmikroskop. Majoriteten av de dekonvolutionsexperiment som rapporteras i litteraturen gäller dock bilder som registrerats i ett standard widefield-fluorescensmikroskop.

Källor till bildförstöring

Bildförstöring kan delas in i fyra oberoende källor: brus, spridning, bländning och oskärpa. I figur 2 visas exempel på den visuella effekten av var och en av dessa på samma bild.

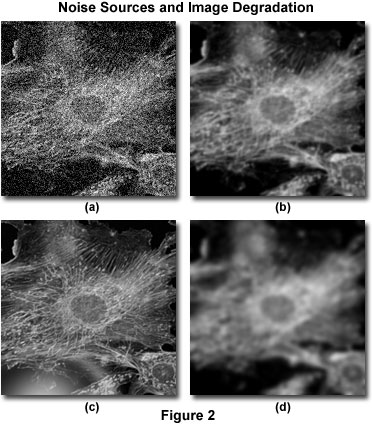
Brus kan beskrivas som en kvasirandomisering av detaljerna i en bild, som (i sin allvarligaste form) ser ut som vitt brus eller salt- och pepparbrus, liknande det som man ser i TV-sändningar med dålig mottagning (figur 2 a)). Denna typ av brus kallas ”kvasirandom” eftersom den statistiska fördelningen kan förutsägas om källans mekanik är känd. I digital mikroskopi är den huvudsakliga källan till brus antingen själva signalen (ofta kallad fotonskottbrus) eller det digitala bildbehandlingssystemet. Man känner till mekaniken hos båda bruskällorna och därför är den statistiska fördelningen av bruset känd. Signalberoende brus kan karakteriseras av en Poisson-fördelning, medan brus som härrör från avbildningssystemet ofta följer en Gauss-fördelning. Eftersom källan till och fördelningen av vanligt brus i digitala bilder är så välkänd kan det lätt avlägsnas genom tillämpning av lämpliga bildfilter, som vanligtvis ingår i de flesta programvarupaket för dekonvolution som en valfri ”förbehandlingsrutin”.

Spridning brukar vanligtvis betecknas som en slumpmässig störning av ljuset som induceras av förändringar i brytningsindexet i hela provet. Nettoeffekten av spridningen är en verkligt slumpmässig förvirring av bilddetaljerna, vilket framgår av figur 2(b). Även om ingen helt tillfredsställande metod har utvecklats för att förutsäga spridningen i en viss provkropp har det visat sig att graden av spridning är starkt beroende av provkroppens tjocklek och de optiska egenskaperna hos provkroppen och de omgivande inbäddningsmaterialen. Spridningen ökar både med provets tjocklek och med heterogeniteten i brytningsindexet hos de interna komponenterna i ett prov.

Som liknar spridning är bländning en slumpmässig störning av ljuset, men den uppstår i mikroskopets optiska element (linser, filter, prismor etc.) snarare än i provet. Nivån av bländning i ett modernt mikroskop har minimerats genom användning av linser och filter med antireflekterande beläggningar och genom förfining av tekniker för formning av linser, optisk cement och glasformuleringar. Figur 2(c) illustrerar effekten av okontrollerad bländning.

Blur beskrivs som en icke slumpmässig spridning av ljuset som uppstår vid passage genom bildsystemets optiska väg (figur 2(d)). Den viktigaste källan till oskärpa är diffraktion, och en bild vars upplösning endast begränsas av oskärpa anses vara diffraktionsbegränsad. Detta utgör en inneboende gräns för alla bildsystem och är den avgörande faktorn vid bedömningen av upplösningsgränsen för ett optiskt system. Lyckligtvis finns det sofistikerade modeller för oskärpa i ett optiskt mikroskop som kan användas för att fastställa källan till fotoner utanför fokus. Detta är grunden för dekonvolution. På grund av dess grundläggande betydelse för dekonvolution kommer den teoretiska modellen för oskärpa att diskuteras mycket mer ingående i andra delar av detta avsnitt. Det bör dock betonas att alla bildsystem producerar oskärpa oberoende av andra former av bildförstöring som orsakas av provet eller medföljande instrumentelektronik. Det är just detta oberoende av optisk oskärpa från andra typer av försämring som gör det möjligt att avlägsna oskärpa med hjälp av dekonvolutionstekniker.

I interaktionen mellan ljus och materia ligger det primära fysiska ursprunget till spridning, bländning och oskärpa. Sammansättningen och arrangemanget av molekyler i ett visst material (oavsett om det är glas, vatten eller protein) ger varje material en egen uppsättning optiska egenskaper. När det gäller dekonvolution är det som skiljer spridning, bländning och oskärpa från varandra den plats där de uppstår och möjligheten att skapa en matematisk modell för dessa fenomen. Eftersom spridning är ett lokaliserat, oregelbundet fenomen som förekommer i provet har det visat sig vara svårt att modellera. Eftersom oskärpa däremot är en funktion av mikroskopets optiska system (främst objektivet) kan den modelleras relativt enkelt. En sådan modell gör det möjligt att matematiskt vända oskärpa-processen, och dekonvolution använder denna modell för att vända eller ta bort oskärpa.

Punktspridningsfunktionen

Den modell för oskärpa som har utvecklats inom teoretisk optik bygger på begreppet tredimensionell punktspridningsfunktion (PSF). Detta begrepp är av grundläggande betydelse för dekonvolution och bör förstås klart och tydligt för att undvika bildartefakter. Punktspridningsfunktionen bygger på en oändligt liten punktljuskälla med ursprung i provets (objektets) utrymme. Eftersom mikroskopets bildsystem endast samlar in en bråkdel av det ljus som sänds ut av denna punkt, kan det inte fokusera ljuset till en perfekt tredimensionell bild av punkten. Istället ser punkten ut att vara breddad och spridd i ett tredimensionellt diffraktionsmönster. Således definieras punktspridningsfunktionen formellt som det tredimensionella diffraktionsmönster som genereras av en ideal punktljuskälla.

Avhängigt av det avbildningsläge som används (widefield, konfokalt, genomlyst ljus) har punktspridningsfunktionen en annan och unik form och kontur. I ett widefield-fluorescensmikroskop liknar formen på punktspridningsfunktionen en avlång ”fotboll” av ljus som omges av en flare av vidgade ringar. För att beskriva punktspridningsfunktionen i tre dimensioner är det vanligt att använda ett koordinatsystem med tre axlar (x, y och z) där × och y är parallella med provets fokalplan och z är parallellt med mikroskopets optiska axel. I det här fallet framträder punktspridningsfunktionen som en uppsättning koncentriska ringar i x-y-planet och liknar ett timglas i x-z- och y-z-planet (se figur 3). Ett x-y snitt genom centrum av punktspridningsfunktionen med brett fält avslöjar en uppsättning koncentriska ringar: den så kallade Airy-skivan som ofta refereras i texter om klassisk optisk mikroskopi.

Två x-z-projektioner av punktspridningsfunktioner som uppvisar olika grader av sfärisk aberration presenteras i figur 3. Den optiska axeln är parallell med bildens vertikala axel. Punktspridningsfunktionen till vänster visar minimal sfärisk aberration, medan den till höger visar en betydande grad av aberration. Observera att den axiella asymmetrin och breddningen av den centrala noden längs den optiska axeln i den högra bilden leder till försämrad axiell upplösning och suddig signal. I teorin är storleken på punktspridningsfunktionen oändlig, och den totala summerade ljusintensiteten i plan långt från fokus är lika med den summerade intensiteten vid fokus. Ljusintensiteten sjunker dock snabbt och blir så småningom omöjlig att skilja från brus. I en oavbruten punktspridningsfunktion som registrerats med ett oljeimmersionsobjektiv med hög numerisk öppning (1,40) sprids ljus som upptar 0,2 kvadratmikrometer i fokusplanet över 90 gånger den ytan 1 mikrometer ovanför och under fokus. Det prov som användes för att registrera dessa bilder med punktspridningsfunktion var en fluorescerande pärla med en diameter på 0,1 mikrometer monterad i glycerol (brytningsindex lika med 1,47), med immersionsoljor med de brytningsindex som anges i figuren.

En viktig aspekt är hur punktspridningsfunktionen påverkar bildbildningen i mikroskopet. I den teoretiska modellen för bildbildning behandlas punktspridningsfunktionen som den grundläggande enheten i en bild. Med andra ord är punktspridningsfunktionen för bilden vad tegelstenen är för huset. Det bästa en bild någonsin kan bli är en sammansättning av punktspridningsfunktioner, och en ökad förstoring ändrar inte detta faktum. Som en välkänd lärobok i teoretisk optik (Born och Wolf: Principles of Optics) förklarar: ”Det är omöjligt att framhäva detaljer som inte finns i den primära bilden genom att öka okularets styrka, för varje element i den primära bilden är ett litet diffraktionsmönster, och den faktiska bilden, så som den ses av okularet, är bara en helhet av de förstorade bilderna av dessa mönster”.

Som exempel kan man tänka sig en population av fluorescerande partiklar med låg upplösning som är inklämda mellan ett täckglas och ett mikroskopglas. En bild i fokus av detta exemplar avslöjar ett moln av prickar, som i själva verket är en skiva omgiven av en liten uppsättning ringar (i själva verket en Airy-skiva, se figur 4(a)). Om detta prov avlägsnas något från fokus, kommer en större uppsättning koncentriska ringar att visas där varje prick fanns i den fokuserade bilden (figur 4(b)). När en tredimensionell bild av detta prov samlas in registreras en fullständig punktspridningsfunktion för varje pärla. Punktspridningsfunktionen beskriver vad som händer med varje punktkälla av ljus efter att den passerat genom bildsystemet.

Den oskärpa som just beskrevs är matematiskt modellerad som en konvolution. Konvolutionen beskriver tillämpningen av punktspridningsfunktionen på varje punkt i provet: ljuset som sänds ut från varje punkt i objektet konvolveras med punktspridningsfunktionen för att producera den slutliga bilden. Tyvärr leder denna konvolution till att punkterna i provet blir suddiga områden i bilden. Ljusstyrkan hos varje punkt i bilden är linjärt relaterad genom konvolutionen till fluorescensen hos varje punkt i provet. Eftersom punktspridningsfunktionen är tredimensionell är oskärpa från punktspridningsfunktionen ett tredimensionellt fenomen. Bilden från varje fokalplan innehåller suddigt ljus från punkter som ligger i det planet blandat med suddigt ljus från punkter som har sitt ursprung i andra fokalplan.

Situationen kan sammanfattas med tanken att bilden bildas genom en konvolution av provet med punktspridningsfunktionen. Dekonvolutionen vänder på denna process och försöker rekonstruera provet från en suddig bild.

Aberrationer i punktspridningsfunktionen

Punktspridningsfunktionen kan definieras antingen teoretiskt genom att använda en matematisk modell för diffraktion eller empiriskt genom att förvärva en tredimensionell bild av en fluorescerande pärla (se figur 3). En teoretisk punktspridningsfunktion har i allmänhet axial och radiell symmetri. Punktspridningsfunktionen är alltså symmetrisk över och under x-y-planet (axial symmetri) och roterande runt z-axeln (radiell symmetri). En empirisk punktspridningsfunktion kan avvika avsevärt från perfekt symmetri (se figur 3). Denna avvikelse, som vanligen kallas aberration, orsakas av oegentligheter eller feljusteringar i någon komponent i bildsystemets optiska system, särskilt objektivet, men kan också uppstå med andra komponenter som speglar, stråldelare, tublinser, filter, bländare och bländare. Ju högre kvalitet på de optiska komponenterna och ju bättre mikroskopinriktningen är, desto närmare kommer den empiriska punktspridningsfunktionen sin ideala symmetriska form. Både konfokal och dekonvolutionsmikroskopi är beroende av att punktspridningsfunktionen ligger så nära idealfallet som möjligt.

Den vanligaste aberrationen som man stöter på vid optisk mikroskopi och som är välkänd för alla erfarna och professionella mikroskopister är sfärisk aberration. Manifestationen av denna aberration är en axiell asymmetri i formen av punktspridningsfunktionen, med en motsvarande ökning av storleken, särskilt längs z-axeln (figur 3). Resultatet är en betydande förlust av upplösning och signalintensitet. I praktiken är den typiska källan till sfärisk aberration en bristande överensstämmelse mellan brytningsindexen hos objektivets frontlinsens doppningsmedium och det monteringsmedium i vilket provet badar. Man bör lägga stor vikt vid vikten av att minimera denna aberration. Även om dekonvolution delvis kan återställa förlorad upplösning kan ingen bildbehandling återställa förlorad signal.