Articles / januari 22, 2022

Introduktion av konsistent hashing

30 april, 2020 – 11 min read

Som en snabb introduktion till hash är det viktigt att förstå att huvudidén handlar om att sprida värden över ett område. Till exempel:

MD5 sprider värden över en 128-bitars rymddomän
En hashtable (eller hashmap) som backas upp av en array med 32 element har en intern hashfunktion som sprider värden till valfritt index (från 0 till 31).

Lastfördelning

Lastfördelning kan definieras som processen för att sprida belastning över noder. Termen nod är här utbytbar mot server eller instans. Det är en beräkningsenhet.

Lastbalansering är ett exempel på lastfördelning. Det handlar om att fördela en uppsättning uppgifter över en uppsättning resurser. Till exempel använder vi lastbalansering för att fördela API-förfrågningar mellan webbserverinstanser.

När det gäller data använder vi hellre termen sharding. En databas shard är en horisontell partition av data i en databas. Ett typiskt exempel är en databas som är uppdelad i tre shards där varje shard har en delmängd av de totala uppgifterna.

Lastbalansering och sharding har vissa gemensamma utmaningar. Att sprida data jämnt till exempel för att garantera att en nod inte blir överbelastad jämfört med de andra. I vissa sammanhang måste lastbalansering och sharding också fortsätta att associera uppgifter eller data till samma nod:

Om vi behöver serialisera, hantera en efter en, operationerna för en viss konsument måste vi dirigera förfrågan till samma nod.
Om vi behöver distribuera data måste vi veta vilken shard som är ägare till en viss nyckel.

Låter det bekant? I dessa två exempel sprider vi värden över en domän. Oavsett om det är en uppgift som sprids till servernoder eller data som sprids till databas shard, hittar vi tillbaka till idén som är förknippad med hashing. Detta är anledningen till att hashing kan användas tillsammans med lastfördelning. Låt oss se hur.

Mod-n Hashing

Principen för mod-n hashing är följande. Varje nyckel hashas med hjälp av en hashfunktion för att omvandla en inmatning till ett heltal. Därefter utförs en modulo baserad på antalet noder.

Låt oss se ett konkret exempel med 3 noder. Här behöver vi fördela belastningen mellan dessa noder baserat på en nyckelidentifierare. Varje nyckel hashedas och sedan utför vi en modulo-operation:

Fördelen med det här tillvägagångssättet är att det är statslöst. Vi behöver inte behålla något tillstånd för att påminna oss om att foo har dirigerats till nod 2. Ändå måste vi veta hur många noder som är konfigurerade för att tillämpa modulooperationen.

Hur fungerar mekanismen i händelse av skalning ut eller in (lägga till eller ta bort noder)? Om vi lägger till ytterligare en nod baseras modulooperationen nu på 4 istället för 3:

Som vi kan se är nycklarna foo och baz inte längre associerade med samma nod. Med mod-n hashing finns det ingen garanti för att upprätthålla någon konsistens i associeringen mellan nyckel och nod. Är detta ett problem? Det kan det vara.

Vad händer om vi implementerar ett datalagret med hjälp av sharding och baserat på mod-n-strategin för att distribuera data? Om vi skalar antalet noder måste vi utföra en ombalansering. I det tidigare exemplet innebär ombalansering:

Förflyttning av foo från nod 2 till nod 0.
Förflyttning av baz från nod 2 till nod 3.

Nu, vad händer om vi hade lagrat miljontals eller till och med miljarder data och att vi behöver ombalansera nästan allt? Som vi kan föreställa oss skulle detta vara en tung process. Därför måste vi ändra vår teknik för lastfördelning för att se till att vid ombalansering:

Fördelningen förblir så jämn som möjligt baserat på det nya antalet noder.
Antalet nycklar som vi måste migrera bör vara begränsat. Helst skulle det bara vara 1/n procent av nycklarna där n är antalet noder.

Detta är exakt syftet med konsekventa hash-algoritmer.

Termen konsekvent kan dock vara något förvirrande. Jag har träffat ingenjörer som antog att sådana algoritmer fortsatte att associera en viss nyckel till exakt samma nod även när det gäller skalbarhet. Detta är inte fallet. Den måste vara konsekvent fram till en viss punkt för att hålla fördelningen enhetlig.

Nu är det dags att gräva i några lösningar.

Rendezvous

Rendezvous var den första algoritmen som någonsin föreslogs för att lösa vårt problem. Även om den ursprungliga studien, som publicerades 1996, inte nämnde termen consistent hashing, ger den en lösning på de utmaningar vi beskrev. Låt oss se en möjlig implementering i Go:

Hur fungerar den? Vi går igenom varje nod och beräknar dess hashvärde. Hashvärdet returneras av en hash-funktion som producerar ett heltal baserat på en nyckel (vår inmatning) och en nodidentifierare (den enklaste metoden är att hasha sammanlänkningen av de två strängarna). Därefter returnerar vi noden med det högsta hashvärdet. Detta är anledningen till att algoritmen också är känd som highest random weight hashing.

Den största nackdelen med rendezvous är dess tidskomplexitet O(n) där n är antalet noder. Den är mycket effektiv om vi behöver ha ett begränsat antal noder. Men om vi börjar underhålla tusentals noder kan den börja orsaka prestandaproblem.

Ring Consistent Hash

Nästa algoritm släpptes 1997 av Karger et al. i denna artikel. I denna studie nämns för första gången termen consistent hashing.

Den är baserad på en ring (ett sammanhängande nätverk från början till slut). Även om det är den mest populära algoritmen för konsekvent hashing (eller åtminstone den mest kända) är principen inte alltid väl förstådd. Låt oss dyka ner i den.

Den första operationen är att skapa ringen. En ring har en fast längd. I vårt exempel delar vi upp den i 12 delar:

Därefter placerar vi våra noder. I vårt exempel kommer vi att definiera N0, N1 och N2.

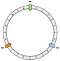
Noderna är jämnt fördelade för tillfället. Vi kommer att återkomma till denna punkt senare.

Då är det dags att se över hur nycklarna ska representeras. Först behöver vi en funktion f som returnerar ett ringindex (från 0 till 11) baserat på en nyckel. Vi kan använda mod-n hashing för detta. Eftersom ringlängden är konstant kommer det inte att orsaka oss några problem.

I vårt exempel kommer vi att definiera 3 nycklar: a, b och c. Vi tillämpar f på var och en av dem. Låt oss anta att vi får följande resultat:

f(a) = 1
f(a) = 5
f(a) = 7

Därmed kan vi placera nycklarna på ringen på detta sätt:

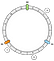
Hur kopplar vi en given nyckel till en nod? Huvudlogiken är att gå framåt. Från en given nyckel returnerar vi den första noden som vi hittar härnäst medan vi går framåt:

I det här exemplet associerar vi a till N1, b och c till N2.

Nu ska vi se hur ombalansering hanteras. Vi definierar ytterligare en nod N3. Var ska vi placera den? Det finns inget utrymme för att den övergripande fördelningen ska vara enhetlig längre. Ska vi omorganisera noderna? Nej, annars skulle vi inte längre vara enhetliga, eller hur? För att placera en nod återanvänder vi samma hashfunktion f som vi introducerade. Istället för att anropas med en nyckel kan den anropas med en nodidentifierare. Så positionen för den nya noden bestäms slumpmässigt.

En fråga uppstår då: vad ska vi göra med a eftersom nästa nod inte längre är N1:

Lösningen är följande: Vi måste ändra dess association och få a associerad med N3:

Som vi diskuterade tidigare bör en idealisk algoritm ombalansera 1/n procent av nycklarna i genomsnitt. I vårt exempel, eftersom vi lägger till en fjärde nod, bör 25 procent av de möjliga nycklarna omfördelas till N3. Är detta fallet?

N0 från index 8 till 12: 33,3 % av de totala nycklarna
N1 från index 2 till 4: 16,6 % av de totala nycklarna
N2 från index 4 till 8: 33.3 % av det totala antalet nycklar
N3 från index 0 till 2: 16,6 % av det totala antalet nycklar

Fördelningen är inte jämn. Hur kan vi förbättra den? Lösningen är att använda virtuella noder.

Vad sägs om att i stället för att placera en enda punkt per nod kan vi placera tre. Dessutom måste vi definiera tre olika hashfunktioner. Varje nod hashasas tre gånger så att vi får tre olika index:

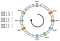
Vi kan tillämpa samma algoritm genom att röra oss framåt. Ändå skulle en nyckel kopplas till en nod oavsett vilken virtuell nod den mötte.

I just det här exemplet skulle fördelningen nu bli följande:

N0: 33,3 %
N1: 25 %
N2: 41,6 %

Desto fler virtuella noder vi definierar per nod, desto mer enhetlig bör fördelningen bli. I genomsnitt, med 100 virtuella noder per server, är standardfördelningen cirka 10 %. Med 1000 är den cirka 3,2 %.

Denna mekanism är också användbar om vi har noder med olika storlek. Om en nod till exempel är konfigurerad för att teoretiskt sett kunna hantera två gånger större belastning än de andra kan vi sätta upp dubbelt så många virtuella noder.

Den största nackdelen med de virtuella noderna är dock minnesavtrycket. Om vi måste hantera tusentals servrar skulle det kräva megabyte av minne.

För att gå vidare är det intressant att notera att en algoritm ibland kan förbättras avsevärt genom att ändra en liten del. Detta är till exempel fallet med en algoritm som publicerades av Google 2017 och som kallas consistent hashing with bounded loads. Denna version bygger på samma ringidé som vi beskrev. Men deras tillvägagångssätt är att utföra en liten ombalansering vid varje uppdatering (en ny nyckel eller nod som läggs till eller tas bort). Denna version överträffar den ursprungliga i termer av standardavvikelse med kompromiss av en värsta tidskomplexitet.

Jump Consistent Hash

År 2007 publicerade två ingenjörer från Google jump consistent hash. Jämfört med den ringbaserade algoritmen kräver denna implementering ”ingen lagring, är snabbare och gör ett bättre jobb med att jämnt fördela nyckelutrymmet mellan hinkarna och att jämnt fördela arbetsbelastningen när antalet hinkar ändras”. Sagt på ett annat sätt förbättrar den fördelningen av arbetsbelastningen mellan noderna (en hink är samma begrepp som en nod) utan någon minnesöverskottskostnad.

Här är algoritmen i C++ (7 rader kod 🤯):

I ringkonsistent hash, med 1 000 virtuella noder, var standardavvikelsen cirka 3,2 %. I jump consistent hash behöver vi inte längre begreppet virtuella noder. Ändå är standardavvikelsen fortfarande mindre än 0,0000001%.

Det finns dock en begränsning. Noderna måste numreras i följd. Om vi har en lista med servrar foo, bar och baz kan vi till exempel inte ta bort bar. Men om vi konfigurerar ett datalager kan vi ändå tillämpa algoritmen för att få fram shardindexet baserat på det totala antalet shards. Därför kan jump consistent hash vara användbar i samband med sharding men inte lastbalansering.

Vad är Perfect Consistent Hashing Algorithm?

När vi nu har en viss erfarenhet av konsekvent hashning kan vi ta ett steg tillbaka och se vad som skulle vara den perfekta algoritmen:

Endast 1/n procent av nycklarna skulle omplaceras i genomsnitt där n är antalet noder.
En O(n) rymdkomplexitet där n är antalet noder.
En O(1) tidskomplexitet per insättning/avlägsnande av en nod och per nyckelsökning.
En minimal standardavvikelse för att se till att en nod inte är överbelastad jämfört med en annan.
Den skulle göra det möjligt att associera en vikt till en nod för att hantera olika nodstorlekar.
Den skulle göra det möjligt att namnge godtyckliga noder (som inte är sekventiellt numrerade) för att stödja både lastbalansering och sharding.

Tyvärr finns denna algoritm inte. Baserat på vad vi såg:

Rendezvous har en linjär tidskomplexitet per sökning.
Ring consistent hash har en dålig minimal standardavvikelse utan begreppet virtuella noder. Med virtuella noder är rymdkomplexiteten O(n*v) där n är antalet noder och v är antalet virtuella noder per nod.
Jump konsekvent hash har inte en konstant tidskomplexitet och stöder inte godtyckliga nodnamn.

Området är fortfarande öppet och det finns nya studier som är värda att titta på. Till exempel den konsekventa hash med flera prover som släpptes 2005. Den stöder O(1) rymdkomplexitet. För att uppnå en standardavvikelse på ε krävs dock O(1/ε) tid per sökning. Om vi till exempel vill uppnå en standardavvikelse på mindre än 0,5 % krävs det att nyckeln hashasheras cirka 20 gånger. Därför kan vi få en minimal standardavvikelse men med ansträngning av en högre tidskomplexitet för uppslag.

Som vi sa i inledningen blev konsekventa hash-algoritmer mainstream. De används nu i otaliga system som MongoDB, Cassandra, Riak, Akka osv. vare sig det gäller balansering av belastning eller fördelning av data. Men som så ofta inom datavetenskap har varje lösning kompromisser.

På tal om kompromisser, om du behöver en uppföljning kan du ta en titt på det utmärkta inlägget skrivet av Damian Gryski:

Universe