Helmholtzresonans
- Analys av Helmholtzresonans
- Resonans, impedans, fas- och frekvensberoende
- Komplikationer som involverar längden
- Helmholtzresonans och gitarrer
Analys av Helmholtzresonans
Låt oss nu bli kvantitativa: Först och främst antar vi att våglängden för det producerade ljudet är mycket längre än resonatorns dimensioner. För flaskorna i animationen högst upp på den här sidan är våglängderna 180 respektive 74 cm, så denna approximation är ganska bra, men det är värt att kontrollera när du börjar beskriva något som en Helmholtzoscillator. Konsekvensen av denna approximation är att vi kan försumma tryckvariationer inom behållarens volym: tryckoscillationen kommer att ha samma fas överallt inom behållaren.
Låt luften i halsen ha en effektiv längd L och en tvärsnittsarea S. Dess massa är då SL gånger luftens densitet ρ. (Vissa komplikationer kring den effektiva längden diskuteras i slutet av denna sida). Om denna ”plugg” av luft sjunker en liten sträcka x ner i flaskan komprimerar den luften i behållaren så att den luft som tidigare upptog volym V nu har volym V – Sx. Följaktligen stiger trycket i denna luft från det atmosfäriska trycket PA till ett högre värde PA + p.
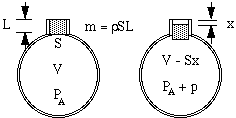
Nu kan man tro att tryckökningen bara skulle vara proportionell mot volymminskningen. Det skulle vara fallet om kompressionen skedde så långsamt att temperaturen inte förändrades. I vibrationer som ger upphov till ljud sker dock förändringarna snabbt och därför stiger temperaturen vid kompressionen, vilket ger en större tryckförändring. Tekniskt sett är de adiabatiska, vilket innebär att värmen inte har någon tid att förflytta sig, och den resulterande ekvationen innefattar en konstant γ, förhållandet mellan de specifika värdena, som är ungefär 1,4 för luft. (Detta förklaras i en bilaga.) Som ett resultat är tryckförändringen p som produceras av en liten volymförändring ΔV bara
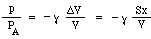
Nu förflyttas massan m av tryckskillnaden mellan halsens övre och nedre del, dvs. en nettokraft pS, så vi skriver Newtons lag för accelerationen a:
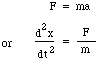
genom att ersätta F och m ger: 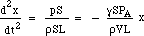
Återställningskraften är alltså proportionell mot förskjutningen. Detta är villkoret för enkel harmonisk rörelse, och den har en frekvens som är 1/2π gånger kvadratroten av proportionalitetskonstanten, så
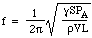
Nu bestäms ljudets hastighet c i luft av densiteten, trycket och förhållandet mellan de specifika värdena, så vi kan skriva:
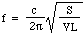
Låt oss sätta in några siffror: för en 1 liters flaska, med S = 3 kvadratcentimeter och L = 5 centimeter, är frekvensen 130 Hz, vilket är ungefär C under C i mitten av C. (Se anteckningar.) Så våglängden är 2,6 meter, vilket är mycket större än flaskan. Detta rättfärdigar, post hoc, det antagande som gjordes i början av härledningen.
Resonans, impedans, fas- och frekvensberoende
Detta avsnitt kan läsas för sig självt, men om du vill ha en mer detaljerad bakgrund, se Oscillationer, forcerade oscillationer och Akustisk följsamhet, tröghet och impedans.
Vi återgår till den mekaniska framställningen och tittar på Helmholtzresonatorn från utsidan, enligt den första schematiska bilden: vi trycker med en oscillerande kraft F, med frekvensen f ,på massan m (luften i resonatorns hals), som stöds av fjädern (den inneslutna luften) med fjäderkonstanten k, vars andra ände är fixerad (luften i resonatorn kan inte fly). Orealistiskt nog försummar vi gravitation och friktion (för tillfället).
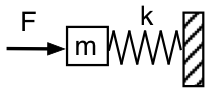
Kraften som krävs för att accelerera massan är proportionell mot accelerationen och därmed proportionell mot f2. Vid tillräckligt låg frekvens är kraften som krävs för att accelerera massan försumbar, så F behöver bara komprimera och utvidga fjädern. I den gränsen är den tillämpade kraften F = +kx. (Fjäderkraften är -kx.) Systemets mekaniska impedans vid denna låga frekvens är följsam eller fjäderliknande. Akustiskt sett ser det ut som en akustisk följsamhet: vi trycker på luftmassan i halsen och komprimerar luften i resonatorn. Den applicerade kraften F till höger är i fas med x mätt till höger, så den ligger 90° bakom hastigheten och det applicerade trycket ligger 90° bakom det akustiska flödet in i resonatorn.
Håll dig till att f2 är beroende av accelerationen. Så vid tillräckligt hög frekvens är fjäderkraften försumbar i jämförelse med den som accelererar massan. F är alltså i fas med accelerationen, vilket gör att den ligger 90° före hastigheten. Akustiskt sett ligger det applicerade trycket 90° före det akustiska flödet in i resonatorn. Det är en mekanisk eller akustisk tröghet.
Vid resonansfrekvensen (vi talar fortfarande om skissen ovan) kan amplituden vara stor för en mycket liten kraft. Så vid resonans är impedansen mycket låg, sett till den kraft som appliceras på massan utifrån (skissen ovan). Vid resonans är flödet in och ut ur resonatorn maximalt.
Och fundera nu på vad som händer om vi tittar på trycket inne i resonatorn (bort från halsen). Här tittar vi på kraften på fjädern, så vår mekaniska analogi ser ut som detta schema.
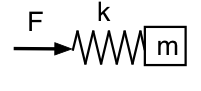
Den här gången innebär den låga frekvensen att kraften kan vara liten för en given amplitud: fjädern och massan rör sig tillsammans som en massa, och systemet ser den här gången trögt ut vid låg frekvens. Vid hög frekvens rör sig massan knappt, och systemet är fjäderliknande eller följsamt. Fasförhållandena är alltså motsatta till vad vi hade tidigare: vid låg f leder p U med 90°; vid hög f släpar p U med 90°.
Komplikationer som involverar den effektiva längden
I det första diagrammet på denna sida ritas ”pluggen” av luft som om den vore en cylinder som slutar snyggt i båda ändarna av flaskhalsen. Detta är förenklat. I praktiken rör sig en extra volym både på insidan och utsidan med luften i halsen – vilket antyds i animationen ovan. Den extra längd som bör läggas till halsens geometriska längd är vanligtvis (och mycket ungefärligt) 0,6 gånger radien i den yttre änden och en radie i den inre änden.)
|
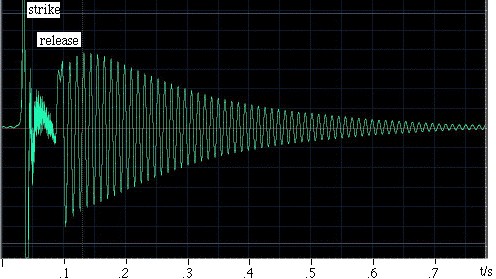
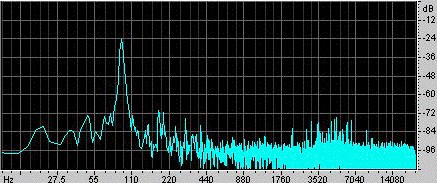
Ett exempel. Ra Inta har gjort detta exempel. Han tog en sfärisk Helmholtzresonator med en volym på 0,00292 m3 och en cylindrisk hals med en längd på 0,080 m och en tvärsnittsarea på 0,00083 m2. För att excitera den slog han på den med handflatan och släppte den sedan. En mikrofon inuti resonatorn registrerar ljudet, som visas i oscillogrammet till vänster. Du kan se att handen tätar resonatorn i ganska mycket mindre än 0,1 s, och att svängningarna under denna tid är svagare och av relativt hög frekvens. När handen släpps etableras en svängning, som gradvis dör bort när den förlorar energi genom visköst och turbulent motstånd och även genom ljudstrålning. En närmare granskning visar att frekvensen stiger något när handen rör sig bort från den öppna änden, eftersom denna hand begränsar den fasta vinkel som är tillgänglig för strålning och därmed ökar ändeffekten (eller ändkorrigeringen). Halsens längd ökas med en bafflad och en icke bafflad ändverkan, vilket ger en effektiv längd på 0,105 m. Med en ljudhastighet på 343 m/s ger uttrycket ovan en resonansfrekvens på 90 Hz. |
|
Helmholtzresonanser och gitarrer
* Jag sade ovan att luften i gitarrkroppen fungerar nästan som en Helmholtzoscillator. Detta fall är komplicerat eftersom kroppen kan svälla lite när lufttrycket stiger inuti – och även eftersom luften ”i” gitarrens ljudhål har en geometri som är mindre lätt att visualisera än den i en flaskhals. När det gäller gitarrkroppen är längden på luftens plugg ungefär lika lång som de två ”ändarna” i slutet av ett ”rör” som bara är ett par mm tjockt. Slutdelarna är dock relaterade till och av liknande storlek som hålets radie, så luftmassan är betydande. Längden på ändan av ett cylindriskt rör som mynnar ut i en oändlig, plan baffel är 0,85 gånger rörets radie. Även om en gitarrs resonansbräda inte är oändlig kan man förvänta sig en liknande slutverkan, och därför skulle den effektiva längden på luftproppen vara ungefär 1,7 gånger hålets radie. (Vissa tillverkare ökar detta genom att fästa ett kort rör under ljudhålet, med samma radie).
Ett par personer har skrivit och frågat hur stort ljudhålet bör vara för ett visst instrument. Vi kan använda ekvationen ovan för att börja besvara den frågan. Det är dock viktigt hur svällande kroppen är. Detta gör luftens ”fjäder” ganska mjukare och sänker därmed frekvensen. Den rena Helmholtzresonansen kan undersökas genom att hålla kroppens volym konstant. När man mäter detta är det vanligt att man begraver gitarren i sand för att hindra kroppens svullnad eller ”andning”. Gitarrer brukar dock inte spelas i denna situation. Helmholtzberäkningen kommer därför att ge en överskattning av resonansfrekvensen för en riktig, flexibel kropp.
Låt oss anta ett cirkulärt ljudhål med radie r, så S = πr2 och L = 1,7r som förklarats ovan. När vi ersätter ekvationen för Helmholtzfrekvensen med c = 340 m/s får vi följande:
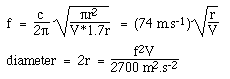
Observera att vi använder standard-SI-enheter: vi har använt ljudets hastighet i meter och sekunder, så volymen måste vara i kubikmeter och frekvensen i Hertz, för att ge ett svar i meter.
Det är mer komplicerat när tonhålen inte är cirkulära, eftersom slutresultatet inte är detsamma som för en cirkel med samma area. Doktoranden och luther John McLennan håller på att skriva en rapport om några mätningar om detta, som vi kommer att publicera här snart.
På instrument från gitarr- och violinfamiljen ligger Helmholtzresonansen (plus kroppen) ofta nära eller lite under frekvensen för den näst lägsta strängen, runt D på en violin eller G-A på en gitarr. Du kan minska eller förskjuta Helmholtzfrekvensen avsevärt genom att täcka hela eller delar av hålet med en lämpligt formad bit styv kartong. Om du sedan spelar en ton nära resonansen och sedan förflyttar kartongen så att den växelvis täcker och avslöjar hålet, kommer du tydligt att höra resonansens effekt.
Är 0,85r-effekten rimlig? Ra Inta, som doktorerade på gitarrakustik i vårt labb, föreslår en intressant demonstration:
Dämpa strängarna på din gitarr så att de inte vibrerar (t.ex. en näsduk mellan strängar och greppbräda). Håll den ena handflatan ovanför ljudhålet och nära det. Med ett finger från den andra handen slår du ett skarpt slag mot klangbrädan nära ljudhålet och nära 1:a strängen. Du kommer att känna en luftpuls på handflatan. Fingrets slag trycker in resonansbordet och pressar ut lite luft ur kroppen. Flytta nu handen gradvis längre bort från hålet och fortsätt att knacka med fingret. När slutar du att känna luftrörelsen? Detta ger dig en grov uppskattning av längden på ”sluteffekten” i fallet med ljudhålet.
Tuning the Helmholtz resonance
Bland publikationerna av John McLennan, doktorand i detta labb, finns en artikel där han varierar Helmholtz-resonansen genom att variera ljudets hastighet.
- McLennan, J.E. (2003) ”A0 and A1 studies on the violin using CO2, He, and air/helium mixtures”. Acustica, 89, 176-180.
Några bilder på historiska Helmholtzresonatorer tillhandahålls av Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply