Green’s Function

Generellt sett, är en grön funktion en integralkärna som kan användas för att lösa differentialekvationer från ett stort antal familjer, inklusive enklare exempel som vanliga differentialekvationer med initial- eller gränsvärdesvillkor, samt svårare exempel som inhomogena partiella differentialekvationer (PDE) med randvillkor. Gröna funktioner är viktiga av flera anledningar och möjliggör visuella tolkningar av de handlingar som är förknippade med en kraftkälla eller med en laddning som är koncentrerad till en punkt (Qin 2014), vilket gör dem särskilt användbara inom områden av tillämpad matematik. I synnerhet används Green’s funktionsmetoder i stor utsträckning inom t.ex, fysik och teknik.

Mer exakt, givet en linjär differentialoperator som verkar på samlingen av fördelningar över en delmängd av ett euklidiskt rum , en Green-funktion i punkten som motsvarar är en lösning av

(1)

där betecknar deltafunktionen. Motiveringen för att definiera en sådan funktion är vitt spridd, men genom att multiplicera ovanstående identitet med en funktion och integrera med avseende på fås

(2)

Den högra sidan reduceras bara till på grund av egenskaper hos deltafunktionen, och eftersom är en linjär operatör som endast verkar på och inte på kan vänstersidan skrivas om till

(3)

Denna reducering är särskilt användbar när man löser för i differentialekvationer av formen

(4)

där ovanstående aritmetik bekräftar att

(5)

och varigenom det följer att har den specifika integralformen

(6)

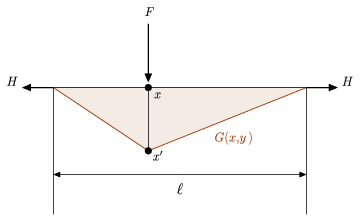
Figuren ovan illustrerar både den intuitiva fysikaliska tolkningen av en grön funktion samt en relativt enkel associerad differentialekvation som man kan jämföra ovanstående definition med (Hartmann 2013). Den visar särskilt ett spänt rep med längden som hänger mellan två väggar och hålls på plats av en identisk horisontell kraft som appliceras på var och en av dess ändar, och en sidobelastning som placeras i någon inre punkt på repet. Låt vara den punkt som motsvarar på det avböjda repet, anta att den nedåtriktade kraften är konstant, säg , och låt beteckna repets avböjning. Motsvarande detta fysiska system är differentialekvationen

(7)

för med , ett system vars enkelhet gör att både dess lösning och dess gröna funktion kan skrivas explicit:

(8)

och

(9)

var för sig. Som framgår av figuren ovan har det förskjutna repet det styckevis linjära formatet som ges av ovan, vilket bekräftar påståendet att Green’s funktion som är associerad med detta system representerar det horisontella repets verkan som motsvarar appliceringen av en kraft .

En Green’s funktion som tar ett par argument kallas ibland för en tvåpunkts Green’s funktion. Detta står i kontrast till flerpunkts-Green’s-funktioner som är av särskild betydelse inom området för teorin om många kroppar.

Som ett elementärt exempel på en tvåpunktsfunktion enligt definitionen ovan kan man betrakta problemet att bestämma potentialen som genereras av en laddningsfördelning vars laddningstäthet är , varvid tillämpningen av Poissons ekvation och Coulombs lag på den potential vid som produceras av varje element med laddningen ger en lösning

(10)

vilket gäller, under vissa villkor, över det område där . Eftersom högersidan kan ses som en integraloperator som omvandlar till , kan man skriva om denna lösning i termer av en grön funktion med formen

(11)

varigenom lösningen kan skrivas om:

(12)

(Arfken 2012).

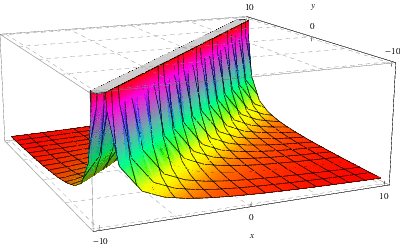
Figuren ovan visar den gröna funktionen som är associerad med lösningen av – ekvationen som diskuterats ovan där här, och , respektive , plottas på -, respektive -, axeln.

En ganska omfattande lista över Gröna funktioner som motsvarar olika differentialekvationer upprätthålls online av Kevin Cole (Cole 2000).

På grund av den mängd litteratur som skrivits om Gröna funktioner kan flera olika notationer och definitioner dyka upp, varav en del är topiskt annorlunda än de ovan nämnda men som i allmänhet inte påverkar de viktiga egenskaperna hos resultaten. Som exemplet ovan illustrerar föredrar till exempel vissa författare att beteckna variablerna och i termer av vektorerna och för att betona det faktum att de är element av för en viss som kan vara större än 1 (Arfken 1985). Det är också relativt vanligt att se definitionen med ett negativt tecken så att definieras som den funktion för vilken

(13)

men på grund av att detta rent fysikaliska övervägande inte har någon effekt på den underliggande matematiken förbises denna synpunkt i allmänhet. Flera andra notationer är också kända för en Greens funktion, varav några inkluderar användningen av en liten bokstav i stället för (Stakgold 1979) samt införandet av ett vertikalt streck i stället för ett kommatecken, t.ex, (Duffy 2001).

I andra fall presenterar litteraturen definitioner som är intimt kopplade till de sammanhang där de presenteras. Vissa författare definierar till exempel Greens funktioner som funktioner som uppfyller en viss uppsättning villkor, t.ex. existens på en speciell typ av domän, association med en mycket speciell differentialoperatör , eller uppfyllande av en exakt uppsättning randvillkor. Ett av de vanligaste exemplen finns i anteckningar av t.ex, Speck, där en grön funktion definieras för att uppfylla för punkterna och för alla punkter som ligger i gränsen av (Speck 2011). Denna särskilda definition presenterar en integralkärna som motsvarar lösningen på en generaliserad Poissons ekvation och skulle därför stöta på uppenbara begränsningar när den anpassas till en mer allmän miljö. Å andra sidan är sådana exempel inte utan fördelar. I fallet med det generaliserade Poisson-exemplet ovan kan till exempel varje sådan grön funktion delas upp så att

(14)

där och för den reguljära laplacianen (Hartman 2013). I sådana situationer kallas för den underliggande differentialekvationens fundamentala lösning och för dess reguljära lösning; som sådan kallas och ibland för den fundamentala respektive reguljära delen av .

Flera grundläggande egenskaper hos en allmän grön funktion följer omedelbart (eller nästan) av dess definition och överförs till alla särskilda fall. Om t.ex. kärnan för operatören är icke-trivial kan det finnas flera Green’s-funktioner associerade till en enda operatör; som ett resultat av detta måste man visa försiktighet när man hänvisar till ”den” Green’s-funktionen. Green’s funktioner uppfyller en adjungerad symmetri i sina två argument så att

(15)

där här definieras som lösningen på ekvationen

(16)

Här är adjungerad till . En omedelbar följd av detta faktum är att för självadjungerade operatörer är symmetrisk:

(17)

Denna identitet kallas ofta för reciprocitetsprincipen och säger, i fysikaliska termer, att responsen vid som orsakas av en enhetskälla vid är densamma som responsen vid som orsakas av en enhetskraft vid (Stakgold 1979).

Den väsentliga egenskapen hos varje grön funktion är att den ger ett sätt att beskriva svaret hos en godtycklig differentialekvationslösning på någon typ av källterm i närvaro av ett visst antal randvillkor (Arfken et al. 2012). Vissa författare anser att en Greens funktion har ungefär samma roll i teorin om partiella differentialekvationer som Fourier-serier i lösningen av vanliga differentialekvationer (Mikula och Kos 2006).

För mer abstrakta scenarier finns ett antal begrepp som fungerar som kontextspecifika analoger till begreppet en Greens funktion. Inom funktionsanalys är det till exempel ofta användbart att betrakta en så kallad generaliserad Green’s funktion som har många analoga egenskaper när den integreras abstrakt mot funktionaler snarare än funktioner. Sådana generaliseringar har faktiskt gett upphov till en helt analog gren av teoretisk PDE-analys och står i sig själva i fokus för en stor mängd forskning.