Articles /

Gram-Schmidt-processen

av Marco Taboga, PhD

Gram-Schmidt-processen (eller förfarandet) är en sekvens av operationer som gör det möjligt att omvandla en uppsättning linjärt oberoende vektorer till en uppsättning ortonormala vektorer som spänner över samma utrymme som den ursprungliga uppsättningen.

Innehållsförteckning

Preliminarier

Låt oss gå igenom några begrepp som är viktiga för att förstå Gram-Schmidt-processen.

Kom ihåg att två vektorer $r$ och $s$ sägs vara ortogonala om och endast om deras inre produkt är lika med noll, det vill säga,

Givet en inre produkt kan vi definiera normen (längden) för en vektor $s$ enligt följande:

En uppsättning vektorer kallas ortonormal om och endast om dess element har enhetsnorm och är ortogonala till varandra. Med andra ord är en uppsättning K vektorer ortonormal om och endast om

Vi har bevisat att vektorerna i en ortonormal uppsättning är linjärt oberoende.

När en bas för ett vektorrum också är en ortonormal uppsättning kallas den för en ortonormal bas.

Projektioner på ortonormala uppsättningar

I Gram-Schmidt-processen använder vi upprepade gånger nästa sats, som visar att varje vektor kan sönderdelas i två delar: 1) dess projektion på en ortonormal uppsättning och 2) en rest som är ortogonal till den givna ortonormala uppsättningen.

Sats Låt $S$ vara ett vektorutrymme utrustat med en inre produkt . Låt vara en ortonormal mängd. För varje $sin S$ har vidär $arepsilon _{S}$ är ortogonal till $u_{k}$ för varje $k=1,ldots ,K.$

Bevis

DefinieraDå har vi för varje $j=1,ldots ,K$ atthär: i stegen $rame{A}$ och $rame{B}$ har vi använt det faktum att den inre produkten är linjär i sitt första argument; I steg $rame{C}$ har vi använt det faktum att om $keq j$ eftersom vi har att göra med en ortonormal mängd; i steg $rame{D}$ har vi använt det faktum att normen för $u_{j}$ är lika med 1. Därför är $arepsilon _{S}$, enligt definitionen ovan, ortogonal till alla element i den ortonormala mängden, vilket bevisar satsen.

Termen kallas den linjära projektionen av $s$ på den ortonormala mängden , medan termen $arepsilon _{S}$ kallas restvärdet av den linjära projektionen.

Normalisering

Ett annat kanske självklart faktum som vi kommer att använda upprepade gånger i Gram-Schmidt-processen är att om vi tar en vektor som inte är noll och vi dividerar den med dess norm, så är resultatet av divisionen en ny vektor som har enhetsnorm.

Med andra ord, om så har vi, genom normens bestämdhetsegenskap, att

Som en följd av detta kan vi definieraoch, genom normens positivitet och absoluta homogenitet, har vi

Översikt över förfarandet

Nu när vi vet hur man normaliserar en vektor och hur man dekomponerar den i en projektion på en ortonormal uppsättning och en rest, är vi redo att förklara Gram-Schmidt-förfarandet.

Vi kommer att ge en översikt över förfarandet, varefter vi kommer att uttrycka det formellt som en sats och vi kommer att diskutera alla tekniska detaljer i beviset för satsen.

Här är översikten.

Vi får en uppsättning linjärt oberoende vektorer .

För att starta processen normaliserar vi den första vektorn, det vill säga vi definierar

I det andra steget projicerar vi $s_{2}$ på $u_{1}$:där $arepsilon _{2}$ är restvärdet av projektionen.

Därefter normaliserar vi restvärdet:

Vi kommer senare att bevisa att (så att normaliseringen kan utföras) eftersom startvektorerna är linjärt oberoende.

De två vektorerna $u_{1}$ och $u_{2}$ som på så sätt erhålls är ortonormala.

I det tredje steget projicerar vi $s_{3}$ på $u_{1}$ och $u_{2}$:och vi beräknar residualen av projektionen $arepsilon _{3}$.

Vi normaliserar den sedan:

Vi fortsätter på detta sätt tills vi får den sista normaliserade residualen $u_{K} $.

I slutet av processen bildar vektorerna en ortonormal uppsättning eftersom:

  1. de är resultatet av en normalisering, och som en följd av detta har de en enhetsnorm;

  2. varje $u_{k}$ erhålls från en rest som har egenskapen att vara ortogonal till .

För att komplettera denna översikt, låt oss komma ihåg att det linjära spannet av är mängden av alla vektorer som kan skrivas som linjära kombinationer av ; det betecknas medoch det är ett linjärt rum.

Eftersom vektorerna är linjärt oberoende kombinationer av , kan alla vektorer som kan skrivas som linjära kombinationer av också skrivas som linjära kombinationer av . Därför sammanfaller spännvidderna för de två uppsättningarna av vektorer:

Formellt uttalande

Vi formaliserar här Gram-Schmidt-processen som ett påstående, vars bevis innehåller alla tekniska detaljer om förfarandet.

Sats Låt $S$ vara ett vektorrum utrustat med en inre produkt . Låt vara linjärt oberoende vektorer. Då finns det en uppsättning ortonormala vektorer så attför varje $kleq K$.

Bevis

Beviset sker genom induktion: först bevisar vi att satsen är sann för $k=1$, och sedan bevisar vi att den är sann för en generisk k om den gäller för $k-1$. När $k=1$ har vektornenhetsnorm och utgör i sig själv en ortonormal mängd: det finns inga andra vektorer, så ortogonalitetsvillkoret är trivialt uppfyllt. Mängdenär mängden av alla skalära multiplar av $s_{1}$, som också är skalära multiplar av $u_{1}$ (och vice versa). Därför Antag nu att satsen är sann för $k-1$. Då kan vi projicera $s_{k}$ på :där restvärdet $arepsilon _{k}$ är ortogonal till . Anta att $arepsilon _{k}=0$. Då,Då vi genom antagandet för varje $jleq k-1$ har vi att för varje $jleq k-1$, där $lpha _{jl}$ är skalarer. Därför,Med andra ord leder antagandet att $arepsilon _{k}=0$ till slutsatsen att $s_{k}$ är en linjär kombination av . Men detta är omöjligt eftersom ett av antagandena i propositionen är att är linjärt oberoende. Som en konsekvens av detta måste det vara så att . Vi kan därför normalisera restvärdet och definiera vektornsom har enhetsnorm. Vi vet redan att $arepsilon _{k}$ är ortogonal till . Detta innebär att även $u_{k}$ är ortogonal till . Således är en ortonormal mängd. Ta nu någon vektor $sin S$ som kan skrivas somdär är skalarer. 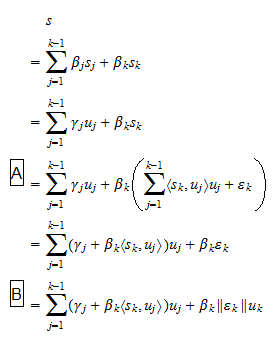Eftersom vi genom antagande har att ekvation (2) också kan skrivas somdär är skalärer, och: i steg $rame{A}$ har vi använt oss av ekvation (1); i steg $rame{B}$ har vi använt oss av definitionen av $u_{k}$. Vi har alltså bevisat att varje vektor som kan skrivas som en linjär kombination av också kan skrivas som en linjär kombination av . Antagandet (3) gör det möjligt att bevisa det omvända på ett helt analogt sätt: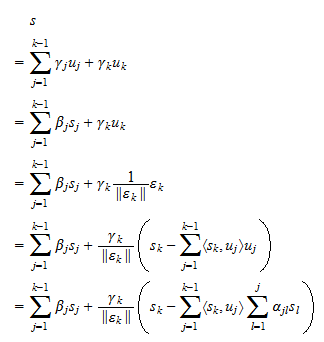Med andra ord är varje linjär kombination av också en linjär kombination av . Detta bevisar att och avslutar beviset.

Varje inre produktrum har en ortonormal bas

Följande sats presenterar en viktig konsekvens av Gram-Schmidt-processen.

Sats Låt $S$ vara ett vektorrum utrustat med en inre produkt . Om $S$ har ändlig dimension finns det en ortonormal bas för $S$.

Bevis

Då $S$ har ändlig dimension, finns det minst en bas för $S$ som består av K vektorer . Vi kan tillämpa Gram-Schmidt-förfarandet på basen och få en ortonormal uppsättning . Eftersom är en bas sträcker den sig över $S$. Därför 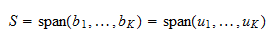Därmed är en ortonormal bas av $S$.

Lösta övningar

Nedan hittar du några övningar med förklarade lösningar.

Övningsuppgift 1

Betrakta rummet $S$ av alla $3imes 1$ vektorer som har reella poster och den inre produktendär $r,sin S$ och $s^{op }$ är transponeringen av $s$. Definiera vektorn

Normalisera $s$.

Lösning

Normen för $s$ ärDärför, är normaliseringen av $s$

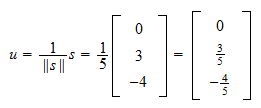
Övningsuppgift 2

Betrakta utrymmet $S$ av alla $2imes 1$ vektorer som har reella poster och den inre produktenvarvid $r,sin S$ . Betrakta de två linjärt oberoende vektorerna

Omvandla dem till en ortonormal uppsättning med hjälp av Gram-Schmidt-processen.

Lösning

Normen för $s_{1}$ är Därför, den första ortonormala vektorn ärDen inre produkten av $s_{2}$ och $u_{1}$ är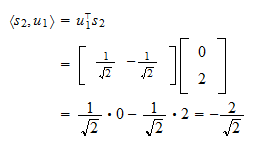Projektionen av $s_{2}$ på $u_{1}$ är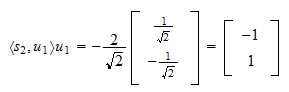Restvärdet av projektionen är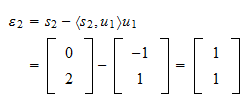Restvärdet äroch det normaliserade restvärdet ärDärmed, den ortonormala mängden vi letade efter är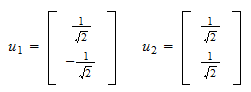

How to cite

Please cite as:

Taboga, Marco (2017). ”Gram-Schmidt process”, Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply