Gibbs Sampling

Som andra MCMC-metoder, konstruerar Gibbs sampler en Markovkedja vars värden konvergerar mot en målfördelning. Gibbs Sampling är i själva verket ett särskilt fall av Metropolis-Hastings-algoritmen där förslag alltid accepteras.

För att utveckla detta antar vi att du vill sampla en multivariat sannolikhetsfördelning.

Notera: En multivariat sannolikhetsfördelning är en funktion av flera variabler (dvs. 2-dimensionell normalfördelning).

Vi vet inte hur vi ska göra ett stickprov från den senare direkt. På grund av någon matematisk bekvämlighet eller kanske bara ren tur råkar vi dock känna till de betingade sannolikheterna.

Det är här Gibbs sampling kommer in. Gibbs Sampling är tillämplig när den gemensamma fördelningen inte är explicit känd eller är svår att ta stickprov från direkt, men den betingade fördelningen av varje variabel är känd och är lättare att ta stickprov från.

Vi börjar med att välja ett startvärde för de slumpmässiga variablerna X & Y. Sedan tar vi stickprov från den betingade sannolikhetsfördelningen av X givet Y = Y⁰ som benämns p(X|Y⁰). I nästa steg tar vi ett urval av ett nytt värde för Y betingat av X¹, som vi just har beräknat. Vi upprepar proceduren i ytterligare n – 1 iterationer och alternerar mellan att dra ett nytt urval från den betingade sannolikhetsfördelningen för X och den betingade sannolikhetsfördelningen för Y, givet det aktuella värdet av den andra slumpvariabeln.

Låtsas oss ta en titt på ett exempel. Anta att vi har följande efterföljande och betingade sannolikhetsfördelningar.

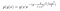
där g(y) innehåller de termer som inte innehåller x, och g(x) innehåller de som inte beror på y.

Vi känner inte till värdet av C (normaliseringskonstant). Vi känner dock till de villkorliga sannolikhetsfördelningarna. Därför kan vi använda Gibbs Sampling för att approximera den efterföljande fördelningen.

Notera: De betingade sannolikheterna är i själva verket normalfördelningar och kan skrivas om på följande sätt.

Med tanke på föregående ekvationer går vi vidare för att implementera Gibbs Sampling-algoritmen i Python. Till att börja med importerar vi följande bibliotek.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Vi definierar funktionen för den efterföljande fördelningen (anta att C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Därefter plottar vi sannolikhetsfördelningen.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Nu ska vi försöka skatta sannolikhetsfördelningen med hjälp av Gibbs Sampling. Som vi nämnde tidigare är de betingade sannolikheterna normalfördelningar. Därför kan vi uttrycka dem i termer av mu och sigma.

I följande kodblock definierar vi funktioner för mu och sigma, initialiserar våra slumpvariabler X & Y och ställer in N (antalet iterationer).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Vi går stegvis igenom Gibbs Sampling-algoritmen.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Slutligen ritar vi resultaten.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Som vi kan se, den sannolikhetsfördelning som erhålls med hjälp av Gibbs Sampling-algoritmen ger en bra approximation av målfördelningen.

Slutsats

Gibbs Sampling är en Monte Carlo Markov Chain-metod som iterativt drar en instans från fördelningen av varje variabel, betingad av de aktuella värdena för de andra variablerna för att uppskatta komplexa gemensamma fördelningar. Till skillnad från Metropolis-Hastings-algoritmen accepterar vi alltid förslaget. Gibbs Sampling kan således vara mycket effektivare.