Friedman-testet i SPSS Statistics
SPSS Statistics
SPSS Statistics Output för Friedman-testet
SPSS Statistics kommer att generera antingen två eller tre tabeller, beroende på om du har valt att få beskrivningar och/eller kvartiler genererade förutom att köra Friedman-testet.
Tabell för deskriptiv statistik
Tabellen för deskriptiv statistik produceras om du har valt alternativet Kvartiler:
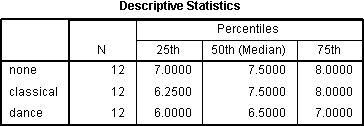
Publicerad med skriftligt tillstånd från SPSS Statistics, IBM Corporation.
Detta är en mycket användbar tabell eftersom den kan användas för att presentera deskriptiv statistik i resultatavsnittet för var och en av tidpunkterna eller förhållandena (beroende på studiens utformning) för din beroende variabel. Denna användbarhet kommer att presenteras i avsnittet ”Redovisning av resultatet” senare.
Rankstabell
Rankstabellen visar den genomsnittliga rangordningen för var och en av de relaterade grupperna, som visas nedan:

Publicerad med skriftligt tillstånd från SPSS Statistics, IBM Corporation.
Friedman-testet jämför medelrankorna mellan de relaterade grupperna och visar hur grupperna skiljer sig åt, och det ingår av denna anledning. Det är dock inte särskilt troligt att du faktiskt kommer att redovisa dessa värden i resultatdelen, utan du kommer troligen att redovisa medianvärdet för varje relaterad grupp.
Teststatistiktabell
Teststatistiktabellen informerar dig om det faktiska resultatet av Friedman-testet och om det fanns en övergripande statistiskt signifikant skillnad mellan de relaterade gruppernas genomsnittsrankor. För det exempel som används i den här guiden ser tabellen ut på följande sätt:

Publicerat med skriftligt tillstånd från SPSS Statistics, IBM Corporation.
Tabellen ovan visar teststatistikvärdet (χ2) (”Chi-square”), frihetsgrader (”df”) och signifikansnivån (”Asymp. Sig.”), vilket är allt vi behöver för att rapportera resultatet av Friedman-testet. I vårt exempel kan vi se att det finns en övergripande statistiskt signifikant skillnad mellan de relaterade gruppernas medelvärden. Det är viktigt att notera att Friedman-testet är ett omnibus-test, liksom dess parametriska alternativ; det vill säga att det talar om huruvida det finns övergripande skillnader, men det anger inte exakt vilka grupper som skiljer sig från varandra. För att göra detta måste du utföra post hoc-tester, vilket kommer att diskuteras efter nästa avsnitt.
SPSS Statistics
Rapportera resultatet av Friedman-testet (utan post hoc-tester)
Du kan rapportera resultatet av Friedman-testet på följande sätt:
- Allmänt
Det fanns en statistiskt signifikant skillnad i den upplevda ansträngningen beroende på vilken typ av musik som lyssnades på när man sprang, χ2(2) = 7.600, p = 0,022.
Du kan också inkludera medianvärdena för varje relaterad grupp. I det här skedet vet du dock bara att det finns skillnader någonstans mellan de relaterade grupperna, men du vet inte exakt var dessa skillnader ligger. Kom dock ihåg att om resultatet av ditt Friedman-test inte var statistiskt signifikant bör du inte köra post hoc-tester.
Post hoc-tester
För att undersöka var skillnaderna faktiskt finns måste du köra separata Wilcoxon signed-rank-tester på de olika kombinationerna av relaterade grupper. I det här exemplet skulle du alltså jämföra följande kombinationer:
- Ingen till klassisk.
- Ingen till dans.
- Klassisk till dans.
Du måste använda en Bonferroni-korrigering på de resultat som du får från Wilcoxon-testerna eftersom du gör flera jämförelser, vilket gör det mer troligt att du kommer att förklara ett resultat som signifikant när du inte borde göra det (ett typ I-fel). Lyckligtvis är Bonferroni-justeringen mycket enkel att beräkna; ta helt enkelt den signifikansnivå som du ursprungligen använde (i det här fallet 0,05) och dividera den med antalet tester som du utför. I det här exemplet har vi alltså en ny signifikansnivå på 0,05/3 = 0,017. Det betyder att om p-värdet är större än 0,017 har vi inte ett statistiskt signifikant resultat.
Om du kör dessa tester (se hur du gör i vår guide för Wilcoxon signed-rank test) på resultaten från det här exemplet får du följande resultat:

Publicerat med skriftligt tillstånd från SPSS Statistics, IBM Corporation.
Denna tabell visar resultatet av Wilcoxon signed-rank-testet för var och en av våra kombinationer. Det är viktigt att notera att signifikansvärdena inte har justerats i SPSS Statistics för att kompensera för flerfaldiga jämförelser – du måste manuellt jämföra de signifikansvärden som SPSS Statistics producerar med den Bonferroni-justerade signifikansnivån som du har beräknat. Vi kan se att vid signifikansnivån p < 0,017 var det bara den upplevda ansträngningen mellan ingen musik och dans (dance-none, p = 0,008) som var statistiskt signifikant annorlunda.
SPSS Statistics
Rapportera resultatet av Friedman-testet (med post hoc-tester)
Du kan rapportera resultatet av Friedman-testet med post hoc-tester på följande sätt:
- Allmänt
Det fanns en statistiskt signifikant skillnad i uppfattad ansträngning beroende på vilken typ av musik som lyssnades på när man sprang, χ2(2) = 7.600, p = 0.022. Post hoc-analys med Wilcoxon signed-rank-test genomfördes med en Bonferroni-korrigering tillämpad, vilket resulterade i en signifikansnivå satt till p < 0,017. Medianen (IQR) för den upplevda ansträngningsnivån för löprundan utan musik, klassisk musik och dansmusik var 7,5 (7-8), 7,5 (6,25-8) respektive 6,5 (6-7). Det fanns inga signifikanta skillnader mellan löprundorna utan musik och med klassisk musik (Z = -0,061, p = 0,952) eller mellan löprundorna med klassisk musik och med dansmusik (Z = -1,811, p = 0,070), trots att den upplevda ansträngningen totalt sett minskade i löprundorna med dans jämfört med klassisk musik. Det fanns dock en statistiskt signifikant minskning av den upplevda ansträngningen i försöket med dansmusik jämfört med försöket utan musik (Z = -2,636, p = 0,008).
Leave a Reply