En lätt introduktion till problemet med konvexa skrov

Konvexa skrov tenderar att vara användbara inom många olika områden, ibland helt oväntat. I den här artikeln förklarar jag den grundläggande idén om 2d konvexa skrov och hur man använder grahamskanning för att hitta dem. Så om du redan känner till grahamscanningen är den här artikeln inte för dig, men om inte bör den här artikeln göra dig bekant med några av de relevanta begreppen.

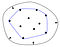
Den konvexa skrovet av en uppsättning punkter definieras som den minsta konvexa polygonen, som omsluter alla punkter i uppsättningen. Konvex innebär att polygonen inte har något hörn som är böjt inåt.

De röda kanterna på den högra polygonen omsluter det hörn där formen är konkav, motsatsen till konvex.

Ett användbart sätt att tänka på det konvexa hullet är gummibandsanalogin. Anta att punkterna i mängden är spikar som sticker ut från en plan yta. Föreställ dig nu vad som skulle hända om du tog ett gummiband och spände det runt spikarna. När gummibandet försöker dra ihop sig till sin ursprungliga längd skulle det omsluta spikarna och röra vid dem som sticker ut längst från centrum.

För att representera det resulterande konvexa skrovet i kod brukar vi lagra listan över punkter som håller upp detta gummiband, dvs. listan över punkter på det konvexa skrovet.

Bemärk att vi fortfarande måste definiera vad som ska hända om tre punkter ligger på samma linje. Om du föreställer dig att gummibandet har en punkt där det rör vid en av spikarna men inte alls böjer sig där, betyder det att spiken där ligger på en rak linje mellan två andra spikar. Beroende på problemet kan vi betrakta denna spik längs den raka linjen som en del av utgången, eftersom den rör vid gummibandet. Å andra sidan kan vi också säga att denna spik inte borde vara en del av resultatet, eftersom gummibandets form inte förändras när vi tar bort det. Detta beslut beror på det problem du för tillfället arbetar med, och det bästa av allt är om du har en indata där inga tre punkter är kollinjära (detta är ofta fallet i enkla uppgifter för programmeringstävlingar) så kan du till och med helt ignorera detta problem.

Finnande av det konvexa skrovet

Om vi tittar på en uppsättning punkter kan vi med hjälp av mänsklig intuition snabbt räkna ut vilka punkter som troligen kommer att röra vid det konvexa skrovet och vilka som kommer att ligga närmare centrum och därmed bort från det konvexa skrovet. Men att översätta denna intuition till kod kräver lite arbete.

För att hitta det konvexa skrovet av en uppsättning punkter kan vi använda en algoritm som kallas Graham Scan, som anses vara en av de första algoritmerna inom beräkningsgeometri. Med hjälp av denna algoritm kan vi hitta den delmängd av punkter som ligger på det konvexa skrovet, tillsammans med den ordning i vilken dessa punkter påträffas när vi går runt det konvexa skrovet.

Algoritmen börjar med att hitta en punkt, som vi med säkerhet vet ligger på det konvexa skrovet. Punkten med den lägsta y-koordinaten kan till exempel anses vara ett säkert val. Om det finns flera punkter vid samma y-koordinat tar vi den som har den största x-koordinaten (detta fungerar även med andra hörnpunkter, t.ex. först lägsta x sedan lägsta y).

Nästan sorterar vi de andra punkterna efter den vinkel de ligger i sett från startpunkten. Om två punkter råkar ligga i samma vinkel ska den punkt som ligger närmare startpunkten förekomma tidigare i sorteringen.

Nu är idén med algoritmen att gå runt i den här sorterade matrisen, och för varje punkt bestämma om den ligger på det konvexa skrovet eller inte. Detta innebär att vi för varje trippel av punkter som vi stöter på bestämmer om de bildar ett konvext eller konkavt hörn. Om hörnet är konkavt vet vi att den mittersta punkten i denna trippel inte kan ligga på det konvexa höljet.

(Observera att termerna konkavt och konvext hörn måste användas i förhållande till hela polygonen, ett hörn i sig självt kan inte vara konvext eller konkavt, eftersom det inte skulle finnas någon referensriktning.)

Vi lagrar de punkter som ligger på det konvexa skrovet på en stapel, på så sätt kan vi lägga till punkter om vi når dem på vår väg runt de sorterade punkterna, och ta bort dem om vi upptäcker att de bildar ett konkavt hörn.

(Strängt taget måste vi komma åt de två översta punkterna i stapeln, därför använder vi en std::vector i stället, men vi tänker på det som en slags stapel, eftersom vi alltid bara är intresserade av de två översta elementen.)

Om vi går runt den sorterade matrisen av punkter lägger vi till punkten till stapeln, och om vi senare kommer fram till att punkten inte tillhör det konvexa höljet, tar vi bort den.

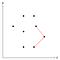
Vi kan mäta om det aktuella hörnet böjer sig inåt eller utåt genom att beräkna korsprodukten och kontrollera om den är positiv eller negativ. Figuren ovan visar en trippel av punkter där hörnet de bildar är konvext, därför stannar den mittersta av dessa tre punkter kvar på stapeln tills vidare.

Om vi går vidare till nästa punkt fortsätter vi att göra samma sak: vi kontrollerar om hörnet är konvext och om det inte är så tar vi bort punkten. Fortsätt sedan att lägga till nästa punkt och upprepa.

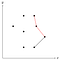
Detta hörn markerat med rött är konkavt, därför tar vi bort den mittersta punkten från stapeln eftersom den inte kan vara en del av det konvexa skrovet.

Hur vet vi att detta ger oss rätt svar?

Att skriva ett rigoröst bevis ligger utanför ramen för den här artikeln, men jag kan skriva ner de grundläggande idéerna. Jag uppmuntrar dig dock att fortsätta och försöka fylla i luckorna!

Då vi beräknade korsprodukten i varje hörn vet vi säkert att vi får en konvex polygon. Nu behöver vi bara bevisa att denna konvexa polygon verkligen innesluter alla punkter.

(Egentligen måste man också visa att detta är den minsta möjliga konvexa polygon som uppfyller dessa villkor, men det följer ganska lätt av att hörnpunkterna i vår konvexa polygon är en delmängd av den ursprungliga mängden punkter.)

Förutsatt att det finns en punkt P utanför den polygon vi just hittat.

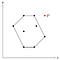
Då varje punkt har lagts till stapeln en gång, vet vi att P togs bort från stapeln vid något tillfälle. Detta innebär att P tillsammans med sina grannpunkter, låt oss kalla dem O och Q, bildade ett konkavt hörn.

Då O och Q ligger innanför polygonen (eller på dess gräns), måste P också ligga innanför gränsen, eftersom polygonen är konvex och det hörn som O och Q bildar tillsammans med P är konkavt i förhållande till polygonen.

Därmed har vi funnit en motsägelse, vilket innebär att en sådan punkt P inte kan finnas.

Implementation

Den här tillhandahållna implementationen har en funktion convex_hull, som tar en std::vector som innehåller punkterna som std::pairs of ints och returnerar en annan std::vector som innehåller de punkter som ligger på det konvexa hullet.

Runtime and memory analysis

Det är alltid användbart att tänka på komplexitetsalgoritmerna i termer av Big-O-notationen, som jag inte kommer att förklara här, eftersom Michael Olorunnisola här redan har gjort ett mycket bättre jobb med att förklara det än vad jag troligen skulle göra:

Att sortera punkterna tar initialt O(n log n)-tid, men efter det kan varje steg beräknas på konstant tid. Varje punkt läggs till och tas bort från stapeln högst en gång, vilket innebär att körtiden i värsta fall ligger på O(n log n).

Minnesanvändningen, som för närvarande ligger på O(n), skulle kunna optimeras genom att ta bort behovet av stapeln och utföra operationerna direkt på inmatningsmatrisen. Vi skulle kunna flytta de punkter som ligger på det konvexa skrovet till början av inmatningsmatrisen och ordna dem i rätt ordning, och de andra punkterna skulle flyttas till resten av matrisen. Funktionen skulle då bara kunna returnera en enda heltalsvariabel som anger antalet punkter i matrisen som ligger på det konvexa höljet. Detta har naturligtvis nackdelen att funktionen blir mycket mer komplicerad, jag skulle därför avråda från det, om du inte kodar för inbäddade system eller har liknande restriktiva minnesproblem. För de flesta situationer är kompromissen mellan felsannolikhet och minnesbesparing helt enkelt inte värd det.

Andra algoritmer

Ett alternativ till Graham Scan är Chans algoritm, som bygger på i stort sett samma idé men är lättare att genomföra. Det är dock klokt att först förstå hur Graham Scan fungerar.

Om du verkligen känner dig fin och vill ta itu med problemet i tre dimensioner kan du ta en titt på Preparatas och Hongs algoritm som presenterades i deras artikel ”Convex Hulls of Finite Sets of Points in Two and Three Dimensions” från 1977.