Del 14 : Dot- och Hadamardprodukt

Och förutom den matrismultiplikation som diskuterats tidigare kan vektorer multipliceras med ytterligare två metoder: Punktprodukt och Hadamardprodukt. De resultat som erhålls med de båda metoderna är olika.

De element som motsvarar samma rad och kolumn multipliceras med varandra och produkterna adderas så att resultatet blir en skalär.

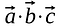
Till skillnad från matrismultiplikation är resultatet av punktprodukten inte en annan vektor eller matris, det är en skalär.

Ordningsföljden på vektorerna spelar ingen roll för punktprodukten, bara antalet element i de båda vektorerna ska vara lika.

Den geometriska formeln för punktprodukt är

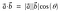
Punktprodukt kallas också inre produkt eller skalär produkt.

Projektion av vektor

Antag att vi har två vektorer c och d som är uppdelade med vinkeln phi(Ф).

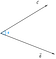
Nu, kan projektionen av vektor c på vektor d representeras som

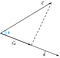
Vi kan dra slutsatsen av figuren att projektionen är lika med den horisontella komponenten av vektor c med avseende på vinkeln phi(Ф).

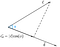
Detta kallas skalär projektion.För att hitta vektorprojektionen av vektor c på vektor d måste vi multiplicera skalärprojektionen med enhetsvektorn d.

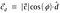
Substituera värdet av enhetsvektorn d.

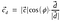
Då, kan punktprodukten också representeras som

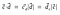
Projektioner har stor användning inom linjär algebra och maskininlärning (Support Vector Machine (SVM) är en algoritm för maskininlärning som används för klassificering av data).

Hadamardprodukt (elementvis multiplikation)

Hadamardprodukt av två vektorer liknar mycket matrisaddition, element som motsvarar samma rad och kolumner i givna vektorer/matriser multipliceras med varandra för att bilda en ny vektor/matris.

Den är uppkallad efter den franske matematikern Jacques Hadamard.

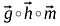
Ordern på matriserna/vektorerna som ska multipliceras bör vara densamma och den resulterande matrisen kommer också att vara av samma ordning.

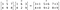
Hadamardprodukt används i tekniker för bildkomprimering som JPEG. Den är också känd som Schurprodukt efter den tyske matematikern Issai Schur.

Hadamardprodukten används i LSTM-celler (Long Short-Term Memory) i Recurrent Neural Networks (RNNs).