Bilinear filtrering och bilinear interpolering

Ta en titt på bilden nedan. Kan du beräkna värdena i punkterna A,B och C?

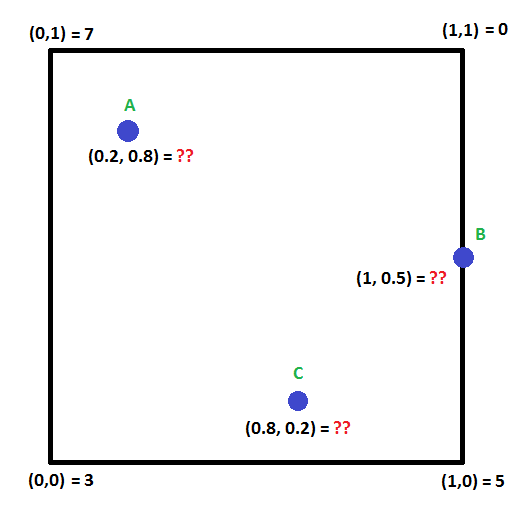
Det finns en teknik för att göra detta som kallas bilinjär interpolation och som utvidgar idén om linjär interpolation till två dimensioner.

För att beräkna bilinjär interpolation gör du bara linjär interpolation på en axel och sedan på den andra.

Kontrollera dessa exempel:

Punkt A
Punkt A har en koordinat på (0,2,0,8). Vi börjar med X-axeln.

Först gör vi en interpolation över toppen av kvadraten på X-axeln. Det innebär att vi måste gå 0,2 (20 %) av vägen från 7 till 0. Denna 0,2 är vår x-axelkoordinat. För att beräkna det gör vi så här:
7 + (0-7) * 0,2 = 5,6

Nästan gör vi en interpolation över den nedre delen av kvadraten på X-axeln. Så i likhet med ovan går vi 0,2 (20 %) av vägen från 3 till 5. För att beräkna det gör vi så här:
3 + (5-3) * 0,2 = 3,4

När vi nu har interpolerat över vår X-axel måste vi interpolera över vår Y-axel. Vi ska nu gå 0,8 (80 %) av vägen från vårt nedre värde (värdet för Y = 0) till vårt övre värde (värdet för Y = 1). Det nedre värdet är den nedre interpolationen vi gjorde (3,4) och det övre värdet är den övre interpolationen vi gjorde (5,6).

Så, vi måste gå 0,8 (80 %) av vägen från 3,4 till 5,6. För att beräkna det gör vi så här:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Så värdet i punkt A är 5,16. Bilden nedan bör hjälpa till att visuellt förklara processen vi gick igenom.

Punkt B

Punkt B har koordinaterna (1,0,0,5).

Låt oss börja med X-axelns interpolation igen (även om du lätt skulle kunna börja med Y först om du vill! Du skulle få samma resultat).

Om vi gör X-axelinterpolationen över toppen måste vi gå 1,0 (100 %) av vägen från 7 till 0. Du kan säkert gissa vad svaret är, men här är det beräknat:
7 + (0-7) * 1,0 = 0

På samma sätt gör vi X-axelinterpolationen över botten. Vi måste gå 1,0 (100 %) av vägen från 3 till 5.
3 + (5-3) * 1,0 = 5

Nästan kommer interpolationen av Y-axeln. Vi måste gå 0,5 (50 %) av vägen från 5 till 0.
5 + (0-5) * 0,5 = 2,5

Där har vi det, värdet i punkt B är 2,5. Det borde också vara begripligt om man tittar på diagrammet. Det är i princip 1d linjär interpolation mellan 5 och 0, och ligger halvvägs mellan dem, så intuitivt borde svaret 2,5 vara vettigt.

Punkt C

Punkt C har en koordinat på (0,8,0,2).

Ennu en gång, låt oss göra X-axelns interpolation över boxens överkant. Vi måste gå 0,8 (80 %) av vägen från 7 till 0.
7 + (0-7) * 0,8 = 1,4

Därefter måste vi göra x-axelinterpolationen över boxens botten. Vi måste gå 0,8 (80 %) av vägen från 3 till 5.
3 + (5-3) * 0,8 = 4,6

Sist, y-axelns interpolation. Vi behöver gå 0,2 (20 %) från 4,6 till 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Värdet för punkt C är 3.96

Bilinjär filtrering

Samtidigt som bilinjär interpolering är användbar om du har ett rutnät av data som du vill interpolera värden inom (t.ex. ett höjdfält som representerar terrängen?!), är det i bilinjär texturfiltrering som den verkligen briljerar i spelutveckling.

I grund och botten, när du har en texturkoordinat som inte är helt i linje med mitten av en pixel i texturen (eftersom det finns en rest), används den bråkiga delen av koordinaten inom den pixeln för att göra en bilinjär interpolation mellan de 4 inblandade pixlarna för att få fram den slutliga pixelfärgen. Den gör bilinjär interpolation på var och en av kanalerna: Rött, grönt, blått och alfa.

Slutresultatet är ganska bra! Kolla in bilden nedan för att se den i aktion på en textur som vi har zoomat in för långt på. Den vänstra sidan använder bilinear filtrering, medan den högra sidan inte gör det och bara visar den närmaste pixeln.

Följaktligen måste bilinear texturfiltrering göra 4 pixelavläsningar för att kunna interpolera mellan dem, i stället för en enda pixelavläsning som när man gör sampling av närmsta pixel. Fler pixelavläsningar = mer overhead, och inte lika billigt (beräkningsmässigt) att använda.

Länkar

För vissa personer som läser det här är den här informationen ganska grundläggande och du kanske undrar varför jag brydde mig om att skriva om det. Titta på nästa inlägg för något ganska bisarrt om bilinear filtrering. Detta behövdes som en språngbräda till nästa sak som jag vill visa er 😛

Wikipedia:

Wikipedia: Linjär interpolation

Wikipedia: Linjär interpolation

Wikipedia: Bilinear interpolation

Wikipedia: Kolla in dessa länkar för djupare information om vissa brister (och vissa lösningar) av hårdvarubaserad bilinear sampling:
iq: hardware interpolation
iq: improved texture interpolation