9.5 – Identifiering av inflytelserika datapunkter

I det här avsnittet lär vi oss följande två mått för att identifiera inflytelserika datapunkter:

• Difference in Fits (DFFITS)
• Cooks avstånd

Den grundläggande idén bakom vart och ett av dessa mått är densamma, nämligen att ta bort observationerna en i taget och varje gång återanpassa regressionsmodellen på de återstående n-1 observationerna. Sedan jämför vi resultaten med hjälp av alla n observationer med resultaten med den i:e observationen borttagen för att se hur stor påverkan observationen har på analysen. Genom att analysera detta kan vi bedöma vilken potentiell påverkan varje datapunkt har på regressionsanalysen.

Difference in Fits (DFFITS)

Differensen i passningar för observation i, betecknad DFFITSi, definieras som:

\

Som du kan se mäter täljaren skillnaden i de förutspådda svaren som erhålls när den i:e datapunkten inkluderas och utesluts från analysen. Nämnaren är den uppskattade standardavvikelsen för skillnaden i de förutspådda svaren. Därför kvantifierar skillnaden i anpassning antalet standardavvikelser som det anpassade värdet förändras när den i:e datapunkten utelämnas.

En observation anses vara inflytelserik om det absoluta värdet av dess DFFITS-värde är större än:

\

där, som alltid, n = antalet observationer och k = antalet prediktortermer (dvs. antalet regressionsparametrar exklusive interceptet). Det är viktigt att komma ihåg att detta inte är en fast regel, utan endast en riktlinje! Det är inte svårt att hitta olika författare som använder en något annorlunda riktlinje. Därför föredrar jag ofta en mycket mer subjektiv riktlinje, t.ex. att en datapunkt anses vara inflytelserik om det absoluta värdet av dess DFFITS-värde sticker ut som en öm tumme från de andra DFFITS-värdena. Naturligtvis är detta en kvalitativ bedömning, kanske som sig bör, eftersom outliers till sin natur är subjektiva storheter.

Exempel nr 2 (igen). Låt oss kontrollera skillnaden i måttet för anpassningar för den här datamängden (influence2.txt):

Regresserar vi y på x och begär skillnaden i anpassningar får vi följande programvaruutdata:

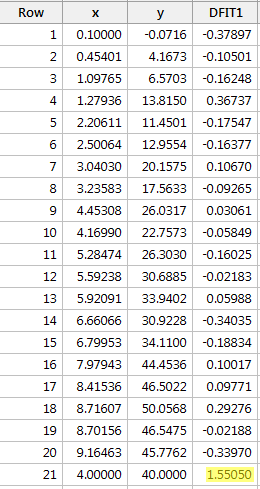
Med hjälp av den objektiva riktlinje som definierats ovan anser vi att en datapunkt är inflytelserik om det absoluta värdet av dess DFFITS-värde är större än:

\

Endast en datapunkt – den röda – har ett DFFITS-värde vars absoluta värde (1.55050) är större än 0,82. Därför, baserat på denna riktlinje, skulle vi betrakta den röda datapunkten som inflytelserik.

Exempel 3 (igen). Låt oss kontrollera skillnaden i passningsmåttet för den här datamängden (influence3.txt):

Regresserar vi y på x och begär skillnaden i anpassningar får vi följande programvaruutdata:

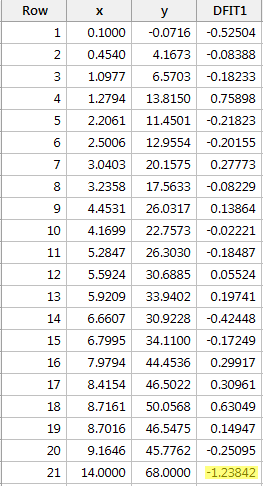
Med hjälp av den objektiva riktlinje som definierats ovan anser vi att en datapunkt är inflytelserik om det absoluta värdet av dess DFFITS-värde är större än:

\

Endast en datapunkt – den röda – har ett DFFITS-värde vars absoluta värde (1.23841) är större än 0,82. Därför skulle vi utifrån denna riktlinje betrakta den röda datapunkten som inflytelserik.

När vi studerade den här datamängden i början av den här lektionen bestämde vi oss för att den röda datapunkten inte påverkade regressionsanalysen så mycket. Men här tyder skillnaden i anpassningsmåttet på att den verkligen är inflytelserik. Vad är det som händer här? Det handlar om att inse att alla mått i den här lektionen bara är verktyg som markerar potentiellt inflytelserika datapunkter för dataanalytikern. I slutändan bör analytikern analysera datamängden två gånger – en gång med och en gång utan de markerade datapunkterna. Om datapunkterna påtagligt ändrar resultatet av regressionsanalysen bör forskaren rapportera resultaten av båda analyserna.

Tillfälligt nog, i det här exemplet här, om vi använder den mer subjektiva riktlinjen om huruvida det absoluta värdet av DFFITS-värdet sticker ut som en öm tumme, är det troligt att vi inte kommer att anse att den röda datapunkten är inflytelserik. Det näst största DFFITS-värdet (i absolut värde) är trots allt 0,75898. Detta DFFITS-värde skiljer sig inte så mycket från DFFITS-värdet för vår ”inflytelserika” datapunkt.

Exempel 4 (igen). Låt oss kontrollera skillnaden i måttet för anpassningar för denna datauppsättning (influence4.txt):

Regresserar vi y på x och begär skillnaden i anpassningar får vi följande programvaruutdata:

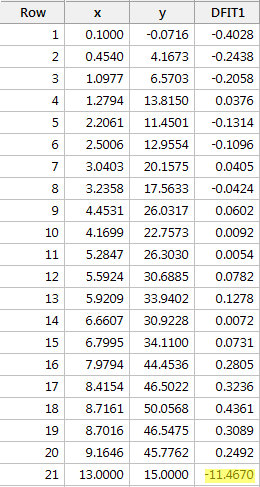
Med hjälp av den objektiva riktlinje som definierats ovan anser vi återigen att en datapunkt är inflytelserik om det absoluta värdet av dess DFFITS-värde är större än:

\

Vad tycker du? Är det något av DFFITS-värdena som sticker ut som en öm tumme? Errr – DFFITS-värdet för den röda datapunkten (-11,4670 ) är definitivt av en annan storleksordning än alla de andra. I det här fallet bör det inte råda något tvivel om att den röda datapunkten är inflytelserik!

Cook’s Distance

Just att hoppa in här, Cooks distansmått, betecknat Di, är definierat som:

\.\]

Det ser lite rörigt ut, men det viktigaste att känna igen är att Cooks Di beror både på restvärdet, ei (i den första termen), och på hävstångseffekten, hii (i den andra termen). Det vill säga, både x-värdet och y-värdet för datapunkten spelar en roll i beräkningen av Cooks avstånd.

Samt sett:

• Di sammanfattar direkt hur mycket alla anpassade värden förändras när den i:e observationen tas bort.
• En datapunkt som har en stor Di indikerar att datapunkten starkt påverkar de anpassade värdena.

Låt oss undersöka vad exakt det första påståendet betyder i samband med några av våra exempel.

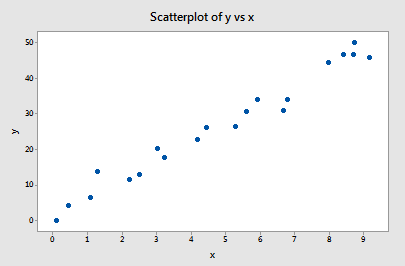
Exempel 1 (igen). Du kanske minns att plottet av dessa data (influence1.txt) tyder på att det inte finns några outliers eller inflytelserika datapunkter för det här exemplet:

Om vi regresserar y på x med hjälp av alla n = 20 datapunkter, fastställer vi att den uppskattade interceptkoefficienten b0 = 1,732 och den uppskattade lutningskoefficienten b1 = 5,117. Om vi tar bort den första datapunkten från datamängden och regresserar y på x med hjälp av de återstående n = 19 datapunkterna, kan vi fastställa att den uppskattade interceptkoefficienten b0 = 1,732 och den uppskattade lutningskoefficienten b1 = 5,1169. Som vi hoppas och förväntar oss förändras skattningarna inte så mycket när vi tar bort den ena datapunkten. Om vi fortsätter denna process med att ta bort varje datapunkt en i taget och plottar de resulterande uppskattade lutningarna (b1) mot de uppskattade avsnitten (b0) får vi:

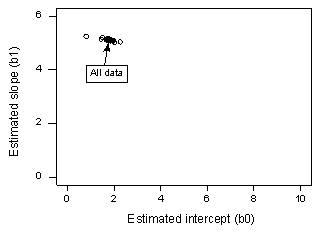
Den heldragna svarta punkten representerar de uppskattade koefficienterna baserade på alla n = 20 datapunkter. De öppna cirklarna representerar var och en av de uppskattade koefficienter som erhålls när man tar bort varje datapunkt en i taget. Som du kan se är de uppskattade koefficienterna alla hopslagna oavsett vilken, om någon, datapunkt som tas bort. Detta tyder på att ingen datapunkt otillbörligt påverkar den uppskattade regressionsfunktionen eller, i sin tur, de anpassade värdena. I det här fallet skulle vi förvänta oss att alla Cooks avståndsmått, Di, skulle vara små.

Exempel 4 (igen). Du kanske minns att diagrammet för dessa data (influence4.txt) tyder på att en datapunkt är inflytelserik och en outlier för det här exemplet:

Om vi regresserar y på x med hjälp av alla n = 21 datapunkter, fastställer vi att den uppskattade interceptkoefficienten b0 = 8,51 och den uppskattade lutningskoefficienten b1 = 3,32. Om vi tar bort den röda datapunkten från datamängden och regresserar y på x med hjälp av de återstående n = 20 datapunkterna, kan vi fastställa att den uppskattade interceptkoefficienten b0 = 1,732 och den uppskattade lutningskoefficienten b1 = 5,1169. Uppskattningarna förändras avsevärt när man tar bort den ena datapunkten. Om vi fortsätter denna process med att ta bort varje datapunkt en i taget och plottar de resulterande uppskattade lutningarna (b1) mot de uppskattade avsnitten (b0) får vi:

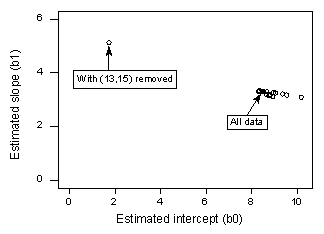
Även här representerar den genomgående svarta punkten de uppskattade koefficienterna baserade på alla n = 21 datapunkter. De öppna cirklarna representerar var och en av de uppskattade koefficienter som erhålls när man tar bort varje datapunkt en i taget. Som du kan se, med undantag för den röda datapunkten (x = 13, y = 15), är de uppskattade koefficienterna alla samlade oavsett vilken, om någon, datapunkt som tas bort. Detta tyder på att den röda datapunkten är den enda datapunkten som otillbörligt påverkar den uppskattade regressionsfunktionen och i sin tur de anpassade värdena. I detta fall skulle vi förvänta oss att Cooks avståndsmått Di för den röda datapunkten skulle vara stort och att Cooks avståndsmått Di för de övriga datapunkterna skulle vara litet.

Användning av Cooks avståndsmått. Det fina med ovanstående exempel är möjligheten att se vad som händer med enkla diagram. Tyvärr kan vi inte förlita oss på enkla plottar när det gäller multipel regression. Istället måste vi förlita oss på riktlinjer för att avgöra när ett Cooks avståndsmått är tillräckligt stort för att motivera att en datapunkt behandlas som inflytelserik.

Här är de riktlinjer som vanligen används:

• Om Di är större än 0,5 är den i:e datapunkten värd att undersökas ytterligare eftersom den kan vara inflytelserik.
• Om Di är större än 1, är det mycket troligt att den it:a datapunkten är inflytelserik.
• Eller, om Di sticker ut som en öm tumme från de andra Di-värdena är det nästan säkert att den är inflytelserik.

Exempel 2 (igen). Låt oss kontrollera Cooks avståndsmått för den här datamängden (influence2.txt):

Regressing y on x and requesting the Cook’s distance measures, we obtain the following software output:

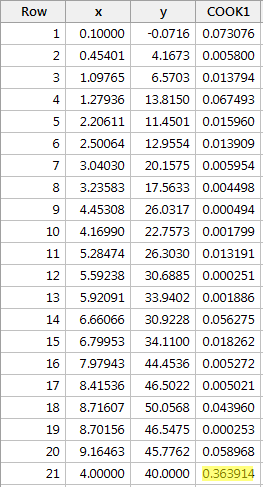
The Cook’s distance measure for the red data point (0.363914) stands out a bit compared to the other Cook’s distance measures. Cook’s avståndsmåttet för den röda datapunkten är ändå mindre än 0,5. Därför skulle vi, baserat på Cooks avståndsmått, inte klassificera den röda datapunkten som inflytelserik.

Exempel 3 (igen). Låt oss kontrollera Cooks avståndsmått för den här datamängden (influence3.txt):

Regressing y on x and requesting the Cook’s distance measures, we obtain the following software output:

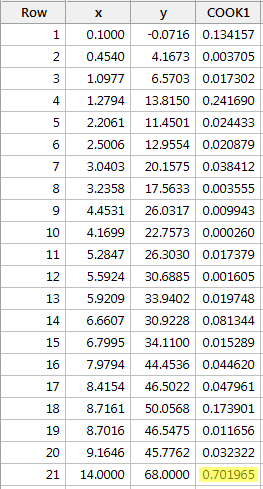
The Cook’s distance measure for the red data point (0.701965) stands out a bit compared to the other Cook’s distance measures. Cooks avståndsmått för den röda datapunkten är dock större än 0,5 men mindre än 1. Därför skulle vi, baserat på Cooks avståndsmått, kanske undersöka ytterligare men inte nödvändigtvis klassificera den röda datapunkten som inflytelserik.

Exempel 4 (igen). Låt oss kontrollera Cooks avståndsmått för den här datamängden (influence4.txt):

Regressing y on x and requesting the Cook’s distance measures, we obtain the following software output:

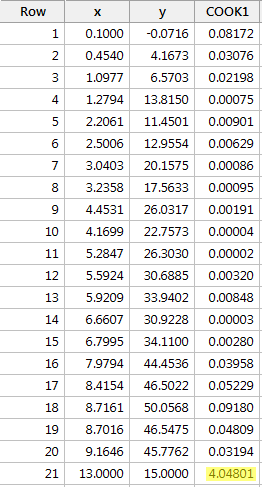
I detta fall är Cooks avståndsmått för den röda datapunkten (4.04801) sticker ut betydligt jämfört med de andra Cook’s distansmåtten. Dessutom är Cooks avståndsmått för den röda datapunkten större än 1. Därför skulle vi baserat på Cooks avståndsmått – och inte överraskande – klassificera den röda datapunkten som inflytelserik.

En alternativ metod för att tolka Cooks avstånd som ibland används är att relatera måttet till F(k+1, n-k-1)-fördelningen och hitta motsvarande percentilvärde. Om detta percentilvärde är mindre än cirka 10 eller 20 procent har fallet ingen uppenbar påverkan på de anpassade värdena. Om det däremot är nära 50 procent eller till och med högre, har fallet ett stort inflytande. (Allt ”däremellan” är mer tvetydigt.)