Rezonanța Helmholtz

• Analiza rezonanței Helmholtz
• Rezonanța, impedanța, dependența de fază și frecvență
• Complicații care implică lungimea
• Rezonanțele Helmholtz și chitarele

Analiza rezonanței Helmholtz

Acum să devenim cantitativi: În primul rând, vom presupune că lungimea de undă a sunetului produs este mult mai mare decât dimensiunile rezonatorului. Pentru sticlele din animația din partea de sus a acestei pagini, lungimile de undă sunt de 180 și, respectiv, 74 cm, deci această aproximare este destul de bună, dar merită verificată ori de câte ori începeți să descrieți ceva ca fiind un oscilator Helmholtz. Consecința acestei aproximări este că putem neglija variațiile de presiune în interiorul volumului recipientului: oscilația presiunii va avea aceeași fază peste tot în interiorul recipientului.

Fie ca aerul din gât să aibă o lungime efectivă L și o arie a secțiunii transversale S. Masa sa este atunci SL ori densitatea aerului ρ. (Unele complicații cu privire la lungimea efectivă sunt discutate la sfârșitul acestei pagini). Dacă acest „dop” de aer coboară o mică distanță x în sticlă, el comprimă aerul din recipient astfel încât aerul care ocupa anterior volumul V are acum volumul V – Sx. În consecință, presiunea acelui aer crește de la presiunea atmosferică PA la o valoare mai mare PA + p.

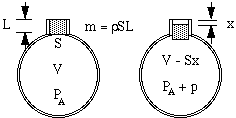
Acum ați putea crede că creșterea presiunii ar fi pur și simplu proporțională cu scăderea volumului. Acesta ar fi cazul dacă comprimarea ar avea loc atât de lent încât temperatura nu s-ar modifica. Cu toate acestea, în cazul vibrațiilor care dau naștere sunetului, schimbările sunt rapide și, prin urmare, temperatura crește la compresie, dând o schimbare mai mare a presiunii. Din punct de vedere tehnic, acestea sunt adiabatice, ceea ce înseamnă că căldura nu are timp să se deplaseze, iar ecuația rezultată implică o constantă γ, raportul dintre căldurile specifice, care este de aproximativ 1,4 pentru aer. (Acest lucru este explicat într-un apendice.) Ca urmare, variația de presiune p produsă de o mică variație de volum ΔV este doar

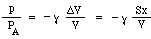
Acum masa m este deplasată de diferența de presiune dintre partea superioară și cea inferioară a gâtului, adică o forță netă pS, așa că scriem legea lui Newton pentru accelerația a:

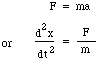
înlocuind F și m se obține: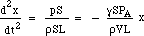

Deci, forța de restabilire este proporțională cu deplasarea. Aceasta este condiția pentru mișcarea armonică simplă, iar aceasta are o frecvență care este de 1/2π ori rădăcina pătrată a constantei de proporționalitate, deci

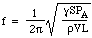
Acum, viteza c a sunetului în aer este determinată de densitate, de presiune și de raportul dintre căldurile specifice, deci putem scrie:

:Să punem câteva cifre: pentru o sticlă de 1 litru, cu S = 3 centimetri pătrați și L = 5 centimetri, frecvența este de 130 Hz, ceea ce reprezintă aproximativ do dedesubt de do central. (Vezi notele.) Deci lungimea de undă este de 2,6 metri, care este mult mai mare decât sticla. Acest lucru justifică, post hoc, ipoteza făcută la începutul derivării.

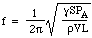
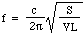
Rezonanță, impedanță, dependență de fază și frecvență

Această secțiune poate fi citită de una singură, dar dacă doriți un context mai detaliat, vedeți Oscilații, Oscilații forțate și Conformitate acustică, inertanță și impedanță.

Să revenim la reprezentarea mecanică și să privim rezonatorul Helmholtz din exterior, așa cum se arată în prima schemă: împingem cu o forță oscilatorie F, cu frecvența f ,masa m (aerul din gâtul rezonatorului), care este sprijinită pe resortul (aerul închis) cu constanta elastică k, al cărui celălalt capăt este fix (aerul din rezonator nu poate scăpa). În mod nerealist, vom neglija gravitația și frecarea (deocamdată).

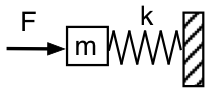
Forța necesară pentru a accelera masa este proporțională cu accelerația și deci proporțională cu f2. La frecvențe suficient de mici, forța necesară pentru a accelera masa este neglijabilă, deci F trebuie doar să comprime și să întindă resortul. Deci, în această limită, forța aplicată F = +kx. (Forța resortului este -kx.) Impedanța mecanică a sistemului la această frecvență joasă este conformă sau asemănătoare cu cea a unui resort. Din punct de vedere acustic, arată ca o complianță acustică: împingem masa de aer din gât și comprimăm aerul din rezonator. Forța F aplicată la dreapta este în fază cu x măsurată la dreapta, deci este la 90° în urma vitezei, iar presiunea aplicată este la 90° în urma fluxului acustic în rezonator.

Amintiți-vă că f2 depinde de accelerație. Deci, la o frecvență suficient de mare, forța arcului este neglijabilă în comparație cu cea care accelerează masa. Deci F este în fază cu accelerația, ceea ce o plasează cu 90° înaintea vitezei. Din punct de vedere acustic, presiunea aplicată este cu 90° înaintea fluxului acustic în rezonator. Este o inertanță mecanică sau acustică.

La frecvența de rezonanță (tot vorbind de schița de mai sus), amplitudinea poate fi mare pentru o forță foarte mică. Deci, la rezonanță, impedanța este foarte mică, privită din punct de vedere al forței aplicate masei din exterior (schema de mai sus). La rezonanță, există un flux maxim în interiorul și în afara rezonatorului.

Considerați acum ce se întâmplă dacă ne uităm la presiunea din interiorul rezonatorului (departe de gât). Aici ne uităm la forța asupra resortului, astfel încât analogul nostru mecanic arată ca în această schemă.

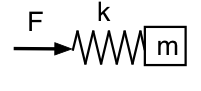
De data aceasta, frecvența joasă înseamnă că forța poate fi mică pentru o amplitudine dată: resortul și masa se mișcă împreună ca o masă, iar sistemul pare de data aceasta inerțial la frecvență joasă. La frecvență înaltă, masa abia se mișcă, iar sistemul este asemănător unui resort sau elastic. Astfel, relațiile de fază sunt opuse față de cele pe care le aveam înainte: la f joasă, p conduce U cu 90°; la f mare, p întârzie U cu 90°.

Complicații care implică lungimea efectivă

Prima diagramă de pe această pagină desenează „dopul” de aer ca și cum ar fi un cilindru care se termină perfect la fiecare capăt al gâtului sticlei. Acest lucru este suprasimplificat. În practică, un volum suplimentar, atât în interior, cât și în exterior, se mișcă odată cu aerul din gât – așa cum sugerează animația de mai sus. Lungimea suplimentară care ar trebui adăugată la lungimea geometrică a gâtului este de obicei (și foarte aproximativ) de 0,6 ori raza de la capătul exterior și o rază la capătul interior).

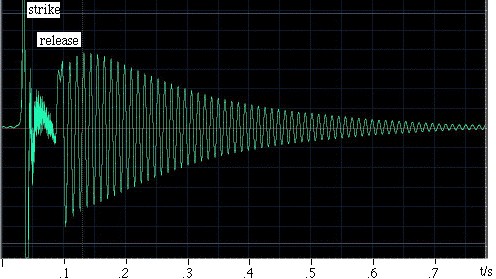
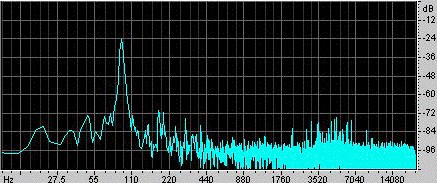
Un exemplu. Ra Inta a făcut acest exemplu. El a luat un rezonator Helmholtz sferic cu un volum de 0,00292 m3 și un gât cilindric cu lungimea de 0,080 m și aria secțiunii transversale de 0,00083 m2. Pentru a-l excita, l-a lovit cu palma mâinii și apoi l-a eliberat. Un microfon din interiorul rezonatorului înregistrează sunetul, care este prezentat în oscilograma din stânga. Se poate observa că mâna sigilează rezonatorul timp de ceva mai puțin de 0,1 s și că, în acest timp, oscilațiile sunt mai slabe și de o frecvență relativ mare.

După ce mâna este eliberată, se stabilește o oscilație, care se stinge treptat pe măsură ce pierde energie prin rezistență vâscoasă și turbulentă, dar și prin radiație sonoră. O examinare atentă arată că frecvența crește ușor pe măsură ce mâna se îndepărtează de capătul deschis, deoarece astfel mâna restrânge unghiul solid disponibil pentru radiație și astfel crește efectul de capăt (sau corecția de capăt).

Lungimea gâtului este mărită cu un efect de capăt cu deflector și unul fără deflector, dându-i o lungime efectivă de 0,105 m. Cu o viteză a sunetului de 343 m/s, expresia de mai sus dă o frecvență de rezonanță de 90 Hz.

Sunetul rezonatorului care este plesnit.

Rezonanțele Helmholtz și chitarele

* Am spus mai sus că aerul din corpul unei chitare se comportă aproape ca un oscilator Helmholtz. Acest caz este complicat deoarece corpul se poate umfla puțin atunci când presiunea aerului crește în interior – și, de asemenea, deoarece aerul „în” gaura de sunet a chitarei are o geometrie care este mai puțin ușor de vizualizat decât cel din gâtul unei sticle. Într-adevăr, în cazul corpului chitarei, lungimea dopului de aer este aproximativ egală cu cele două „efecte finale” de la capătul unei „țevi” care are o grosime de numai câțiva mm. Cu toate acestea, efectele de capăt sunt legate și de dimensiuni similare cu raza orificiului, astfel încât masa de aer este substanțială. Lungimea efectului final al unei țevi cilindrice care se deschide pe un deflector plan și infinit este de 0,85 ori raza țevii. Deși placa de rezonanță a unei chitare nu este infinită, ne putem aștepta la un efect final similar și, prin urmare, lungimea efectivă a „dopului” de aer ar fi de aproximativ 1,7 ori raza găurii. (Unii producători măresc această valoare prin fixarea unui tub scurt sub gaura de sunet, cu o rază egală).

Câteva persoane au scris întrebând cât de mare ar trebui să fie gaura de sunet pentru un anumit instrument. Ei bine, putem folosi ecuația de mai sus pentru a începe să răspundem la această întrebare. Cu toate acestea, umflarea corpului este importantă. Aceasta face ca „elasticitatea” aerului să fie mai degrabă mai moale și astfel scade frecvența. Rezonanța pur Helmholtz poate fi investigată prin menținerea constantă a volumului corpului. Atunci când se măsoară acest lucru, o practică obișnuită este de a îngropa chitara în nisip, pentru a împiedica umflarea sau „respirația” corpului. Cu toate acestea, chitarele nu se cântă de obicei în această situație. Prin urmare, calculul Helmholtz va oferi o supraestimare a frecvenței de rezonanță pentru un corp real, flexibil.

Să presupunem o gaură de sunet circulară cu raza r, deci S = πr2, iar L = 1,7r, așa cum am explicat mai sus. Când înlocuim în ecuația pentru frecvența Helmholtz, folosind c = 340 m/s, obținem:

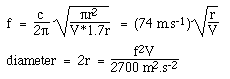
Observați că folosim unități SI standard: am folosit viteza sunetului în metri și secunde, deci volumul trebuie să fie în metri cubi și frecvența în Hertz, pentru a da un răspuns în metri.

Este mai complicat atunci când găurile sonore nu sunt circulare, deoarece efectul final nu este egal cu cel al unui cerc cu aceeași arie. Studentul doctorand și lutierul John McLennan scrie un raport al unor măsurători despre acest lucru, pe care îl vom posta aici în curând.

La instrumentele din familia chitarei și a viorii, rezonanța Helmholtz (plus corpul) este adesea aproape sau puțin sub frecvența celei de-a doua corzi mai joase, în jur de Re la o vioară sau Sol-A la o chitară. Puteți reduce sau deplasa substanțial frecvența Helmholtz prin acoperirea totală sau parțială a găurii cu o bucată de carton rigid de formă adecvată. Dacă apoi cântați o notă aproape de rezonanță și apoi glisați cartonul astfel încât să acopere și să dezvăluie alternativ gaura, veți auzi clar efectul rezonanței.

Este rezonabil efectul de 0,85r? Ra Inta, care a făcut un doctorat pe acustica chitarei în laboratorul nostru, sugerează o demonstrație interesantă:
Umecați corzile chitarei dvs. astfel încât să nu vibreze (de exemplu, o batistă între corzi și claviatură). Țineți palma unei mâini deasupra gurii de sunet, și aproape de ea. Cu un deget al celeilalte mâini, dați o lovitură puternică pe claviatură în apropierea gurii de rezonanță și aproape de prima coardă. Veți simți o pulsație de aer pe palma mâinii dvs. Lovitura cu degetul împinge tabla de rezonanță înăuntru și stoarce o parte din aer din corp. Acum, îndepărtați treptat mâna de gaură și continuați să bateți cu degetul. Când încetați să mai simțiți mișcarea aerului? Acest lucru vă va oferi o estimare aproximativă a lungimii „efectului final” în cazul găurii de sunet.

Tuning the Helmholtz resonance

Printre publicațiile lui John McLennan, doctorand în acest laborator, se numără un articol în care acesta variază rezonanța Helmholtz prin variația vitezei sunetului.

• McLennan, J.E. (2003) „A0 and A1 studies on the violin using CO2, He, and air/helium mixtures”. Acustica, 89, 176-180.

Câteva imagini de rezonatoare Helmholtz istorice furnizate de Thomas B. Greenslade, Kenyon College, Ohio.