Articles /

Procesul Gram-Schmidt

de Marco Taboga, PhD

Procesul (sau procedura) Gram-Schmidt este o secvență de operații care permite transformarea unui set de vectori liniar independenți într-un set de vectori ortonormali care acoperă același spațiu acoperit de setul inițial.

Tabloul de materii

Preliminarii

Să trecem în revistă câteva noțiuni esențiale pentru înțelegerea procedeului Gram-Schmidt.

Amintim că doi vectori $r$ și $s$ se spune că sunt ortogonali dacă și numai dacă produsul lor interior este egal cu zero, adică,

Dat fiind un produs interior, putem defini norma (lungimea) unui vector $s$ după cum urmează: $s$:

Un ansamblu de vectori se numește ortonormal dacă și numai dacă elementele sale au normă unitară și sunt ortogonale între ele. Cu alte cuvinte, un ansamblu de K vectori este ortonormal dacă și numai dacă

Am demonstrat că vectorii unui ansamblu ortonormal sunt liniar independenți.

Atunci când o bază pentru un spațiu vectorial este de asemenea un ansamblu ortonormal, se numește bază ortonormală.

Proiecții pe seturi ortonormale

În procesul Gram-Schmidt, folosim în mod repetat următoarea propoziție, care arată că fiecare vector poate fi descompus în două părți: 1) proiecția sa pe un set ortonormal și 2) un reziduu care este ortogonal la setul ortonormal dat.

Propoziție Fie $S$ un spațiu vectorial echipat cu un produs intern . Fie un ansamblu ortonormal. Pentru orice $sin S$, avem unde $arepsilon _{S}$ este ortogonal cu $u_{k}$ pentru orice $k=1,ldots ,K.$

Probă

DefineAtunci, pentru fiecare $j=1,ldots ,K$, avem căunde: în etapele $cadru{A}$ și $cadru{B}$ am folosit faptul că produsul interior este liniar în primul său argument; în etapa $cadru{C}$ am folosit faptul că dacă $keq j$ deoarece avem de-a face cu un ansamblu ortonormal; în etapa $cadru{D}$ am folosit faptul că norma lui $u_{j}$ este egală cu 1. Prin urmare, $arepsilon _{S}$, așa cum a fost definit mai sus, este ortogonal la toate elementele ansamblului ortonormal, ceea ce dovedește propoziția.

Termenulse numește proiecția liniară a lui $s$ pe ansamblul ortonormal , în timp ce termenul $arepsilon _{S}$ se numește reziduu al proiecției liniare.

Normalizare

Un alt fapt, poate evident, pe care îl vom folosi în mod repetat în procesul Gram-Schmidt este că, dacă luăm orice vector diferit de zero și îl împărțim cu norma sa, atunci rezultatul împărțirii este un nou vector care are normă unitară.

Cu alte cuvinte, dacă atunci, prin proprietatea de definiție a normei, avem că

În consecință, putem definiși, prin pozitivitatea și omogenitatea absolută a normei, avem

Vizualizare generală a procedurii

Acum că știm cum să normalizăm un vector și cum să îl descompunem într-o proiecție pe un ansamblu ortonormal și un reziduu, suntem gata să explicăm procedura Gram-Schmidt.

Vom oferi o prezentare generală a procedeului, după care îl vom exprima formal sub forma unei propoziții și vom discuta toate detaliile tehnice în demonstrația propoziției.

Iată prezentarea generală.

Ni se dă un set de vectori liniar independenți .

Pentru a începe procesul, normalizăm primul vector, adică definim

În al doilea pas, proiectăm $s_{2}$ pe $u_{1}$: unde $arepsilon _{2}$ este reziduul proiecției.

Apoi, normalizăm reziduul:

Vom dovedi ulterior că (pentru ca normalizarea să poată fi efectuată) deoarece vectorii de pornire sunt liniar independenți.

Cei doi vectori $u_{1}$ și $u_{2}$ astfel obținuți sunt ortonormali.

În etapa a treia, proiectăm $s_{3}$ pe $u_{1}$ și $u_{2}$:și calculăm reziduul proiecției $arepsilon _{3}$.

Îl normalizăm apoi:

Procedăm în acest fel până când obținem ultimul reziduu normalizat $u_{K} $.

La sfârșitul procesului, vectorii formează un ansamblu ortonormal deoarece:

  1. ei sunt rezultatul unei normalizări și, în consecință, au normă unitară;

  2. fiecare $u_{k}$ se obține dintr-un reziduu care are proprietatea de a fi ortogonal cu .

Pentru a completa această prezentare generală, să ne amintim că intervalul liniar al lui este ansamblul tuturor vectorilor care pot fi scriși ca combinații liniare ale lui ; se notează cuși este un spațiu liniar.

Deoarece vectorii sunt combinații liniar independente ale lui , orice vector care poate fi scris ca o combinație liniară a lui poate fi scris și ca o combinație liniară a lui . Prin urmare, intervalele celor două seturi de vectori coincid:

Enunț formal

Formalizăm aici procedeul Gram-Schmidt sub forma unei propoziții, a cărei demonstrație conține toate detaliile tehnice ale procedurii.

Propoziție Fie $S$ un spațiu vectorial echipat cu un produs interior . Fie vectori liniar independenți. Atunci, există un ansamblu de vectori ortonormali astfel încâtpentru orice $kleq K$.

Proba

Demonstrarea se face prin inducție: mai întâi dovedim că propoziția este adevărată pentru $k=1$, iar apoi dovedim că este adevărată pentru un k generic dacă este adevărată pentru $k-1$. Când $k=1$, vectorulare normă unitară și constituie prin el însuși un ansamblu ortonormal: nu există alți vectori, deci condiția de ortogonalitate este satisfăcută în mod trivial. Ansambluleste ansamblul tuturor multiplii scalari ai lui $s_{1}$, care sunt, de asemenea, multipli scalari ai lui $u_{1}$ (și viceversa). Prin urmare, Acum, să presupunem că propoziția este adevărată pentru $k-1$. Atunci, putem proiecta $s_{k}$ pe :unde reziduul $arepsilon _{k}$ este ortogonal la . Să presupunem că $arepsilon _{k}=0$. Atunci,Din moment ce, prin ipoteză, pentru orice $jleq k-1$, avem că pentru orice $jleq k-1$, unde $lpha _{jl}$ sunt scalari. Prin urmare,Cu alte cuvinte, ipoteza că $arepsilon _{k}=0$ conduce la concluzia că $s_{k}$ este o combinație liniară de . Dar acest lucru este imposibil deoarece una dintre ipotezele propoziției este că sunt liniar independente. În consecință, trebuie să fie că . Prin urmare, putem să normalizăm reziduul și să definim vectorulcare are normă unitară. Știm deja că $arepsilon _{k}$ este ortogonal la . Aceasta implică faptul că și $u_{k}$ este ortogonal la . Astfel, este un ansamblu ortonormal. Acum, să luăm orice vector $sin S$ care poate fi scris caunde sunt scalari. Deoarece, prin ipoteză, avem că ecuația (2) poate fi scrisă și sub forma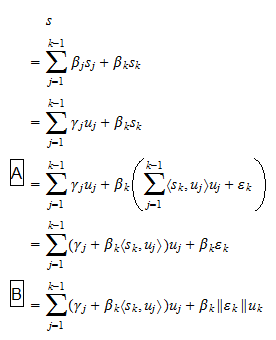unde sunt scalari, și: în pasul $cadrul{A}$ am folosit ecuația (1); în pasul $cadrul{B}$ am folosit definiția lui $u_{k}$. Astfel, am demonstrat că orice vector care poate fi scris ca o combinație liniară a poate fi scris și ca o combinație liniară a . Ipoteza (3) permite demonstrarea inversului într-o manieră complet analogă: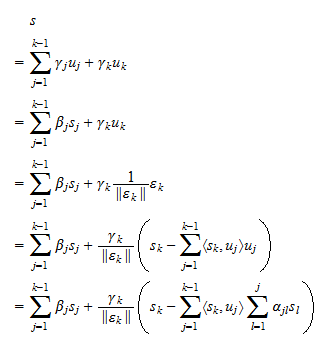Cu alte cuvinte, orice combinație liniară a lui este, de asemenea, o combinație liniară a lui . Aceasta dovedește că și încheie demonstrația.

Care spațiu cu produs interior are o bază ortonormală

Următoarea propoziție prezintă o consecință importantă a procesului Gram-Schmidt.

Propoziție Fie $S$ un spațiu vectorial echipat cu un produs interior . Dacă $S$S are dimensiunea finită , atunci există o bază ortonormală pentru $S$S.

Proba

Din moment ce $S$ este de dimensiune finită, există cel puțin o bază pentru $S$, formată din K vectori . Putem aplica procedura Gram-Schmidt bazei și putem obține un set ortonormal . Deoarece este o bază, aceasta se întinde pe $S$. Prin urmare, 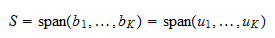Atunci, este o bază ortonormală a lui $S$.

Exerciții rezolvate

Mai jos găsiți câteva exerciții cu soluții explicate.

Exercițiu 1

Se consideră spațiul $S$ al tuturor vectorilor $3imes 1$ cu intrări reale și produsul interiorunde $r,sin S$ și $s^{op }$ este transpunerea lui $s$. Se definește vectorul

Normalizează $s$.

Soluție

Norma lui $s$ esteDeci, normarea lui $s$ este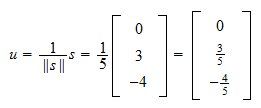

Exercițiu 2

Considerăm spațiul $S$ al tuturor vectorilor $2imes 1$ cu intrări reale și produsul interior unde $r,sin S$ . Se consideră cei doi vectori liniar independenți

Transformați-i într-un ansamblu ortonormal folosind procedeul Gram-Schmidt.

Soluție

Norma lui $s_{1}$ este Deci, primul vector ortonormal esteProdusul intern al lui $s_{2}$ și $u_{1}$ este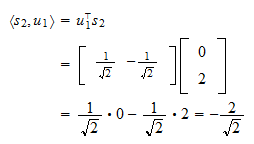Proiecția lui $s_{2}$ pe $u_{1}$ este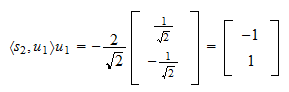Reziduul proiecției este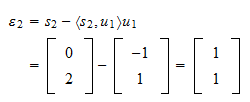Norma reziduului esteși reziduul normalizat esteDeci, setul ortonormal pe care îl căutam este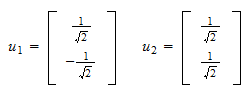

Cum se citește

Citează ca:

Taboga, Marco (2017). „Gram-Schmidt process”, Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply