Partea 14 : Produsul Dot și Hadamard
În afară de înmulțirea matricelor discutată anterior, vectorii pot fi înmulțiți prin alte două metode : Produsul punct și Produsul Hadamard. Rezultatele obținute prin cele două metode sunt diferite.
Elementele corespunzătoare aceluiași rând și aceleiași coloane se înmulțesc între ele, iar produsele se însumează astfel încât, rezultatul să fie un scalar.
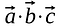
Spre deosebire de înmulțirea matricelor, rezultatul produsului punctat nu este un alt vector sau matrice, ci un scalar.
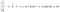
Ordinea vectorilor nu contează pentru produsul punctat, doar numărul de elemente din ambii vectori trebuie să fie egal.
Formula geometrică a produsului punctiform este
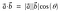
Produsul punctiform se mai numește și produs interior sau produs scalar.
Proiecție de vectori
Să presupunem că avem doi vectori c și d, subțiați de unghiul, phi(Ф).
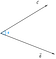
Acum, proiecția vectorului c pe vectorul d ar putea fi reprezentată sub forma
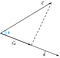
Potem concluziona din figură că proiecția este egală cu componenta orizontală a vectorului c în raport cu unghiul phi(Ф).
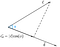
Aceasta se numește proiecție scalară.Pentru a afla proiecția vectorială a vectorului c pe vectorul d trebuie să înmulțim proiecția scalară cu vectorul unitar d.
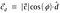
Substituind valoarea vectorului unitar d.
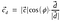
Așa, produsul punct ar putea fi reprezentat, de asemenea, ca
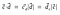
Proiecțiile sunt utilizate pe scară largă în algebra liniară și în învățarea automată (Support Vector Machine(SVM) este un algoritm de învățare automată, utilizat pentru clasificarea datelor).
Produs Hadamard (Element -wise Multiplication)
Produsul Hadamard a doi vectori este foarte asemănător cu adunarea matricelor, elementele care corespund acelorași rânduri și coloane ale vectorilor/matricelor date sunt înmulțite împreună pentru a forma un nou vector/matrice.
Acesta poartă numele matematicianului francez, Jacques Hadamard.
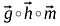
Ordinea matricelor/vehiculelor care urmează să fie înmulțite trebuie să fie aceeași și matricea rezultată va fi, de asemenea, de aceeași ordine.
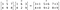

Produsul Hadamard este utilizat în tehnici de compresie a imaginilor, cum ar fi JPEG. Este cunoscut și sub numele de produsul Schur, după numele matematicianului german Issai Schur.
Produsul Hadamard este utilizat în celulele LSTM (Long Short-Term Memory) ale rețelelor neuronale recurente (RNNs).
.
Leave a Reply