O scurtă introducere în confidențialitatea diferențială
.
Aaruran Elamurugaiyan
Privacy poate fi cuantificată. Mai bine, putem clasifica strategiile de păstrare a confidențialității și putem spune care dintre ele este mai eficientă. Și mai bine, putem concepe strategii care sunt robuste chiar și împotriva hackerilor care au informații auxiliare. Și, ca și cum nu ar fi fost suficient de bine, putem face toate aceste lucruri simultan. Aceste soluții, și multe altele, rezidă într-o teorie probabilistică numită confidențialitate diferențială.
Iată contextul. Conservăm (sau gestionăm) o bază de date sensibile și am dori să facem publice unele statistici din aceste date. Cu toate acestea, trebuie să ne asigurăm că este imposibil pentru un adversar să facă inginerie inversă a datelor sensibile din ceea ce am eliberat . În acest caz, un adversar este o parte care are intenția de a dezvălui sau de a afla cel puțin o parte din datele noastre sensibile. Confidențialitatea diferențială poate rezolva problemele care apar atunci când aceste trei ingrediente – date sensibile, curatori care trebuie să elibereze statistici și adversari care doresc să recupereze datele sensibile – sunt prezente (a se vedea figura 1). Această inginerie inversă este un tip de încălcare a confidențialității.

Dar cât de greu este să încalci confidențialitatea? Anonimizarea datelor nu ar fi suficient de bună? Dacă aveți informații auxiliare din alte surse de date, anonimizarea nu este suficientă. De exemplu, în 2007, Netflix a publicat un set de date cu evaluările utilizatorilor săi ca parte a unei competiții pentru a vedea dacă cineva poate depăși algoritmul lor de filtrare colaborativă. Setul de date nu conținea informații de identificare personală, dar cercetătorii au reușit totuși să încalce confidențialitatea; au recuperat 99 % din toate informațiile personale care au fost eliminate din setul de date . În acest caz, cercetătorii au încălcat confidențialitatea folosind informații auxiliare din IMDB.
Cum se poate apăra cineva împotriva unui adversar care are un ajutor necunoscut, și posibil nelimitat, din lumea exterioară? Confidențialitatea diferențială oferă o soluție. Algoritmii cu confidențialitate diferențială sunt rezilienți la atacurile adaptive care utilizează informații auxiliare . Acești algoritmi se bazează pe încorporarea de zgomot aleatoriu în amestec, astfel încât tot ceea ce primește un adversar devine zgomotos și imprecis și, astfel, este mult mai dificil să încalce confidențialitatea (dacă este fezabil).
Contorizarea zgomotoasă
Să ne uităm la un exemplu simplu de injectare a zgomotului. Să presupunem că gestionăm o bază de date de ratinguri de credit (rezumată prin tabelul 1).
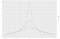
Pentru acest exemplu, să presupunem că adversarul dorește să cunoască numărul de persoane care au un rating de credit prost (care este 3). Datele sunt sensibile, deci nu putem dezvălui adevărul de bază. În schimb, vom folosi un algoritm care returnează adevărul de bază, N = 3, plus niște zgomot aleatoriu. Această idee de bază (adăugarea de zgomot aleatoriu la adevărul de bază) este esențială pentru confidențialitatea diferențială. Să presupunem că alegem un număr aleatoriu L dintr-o distribuție Laplace centrată pe zero, cu o deviație standard de 2. Vom returna N+L. Vom explica alegerea deviației standard în câteva paragrafe. (Dacă nu ați auzit de distribuția Laplace, consultați figura 2). Vom numi acest algoritm „numărare zgomotoasă”.
Dacă vom raporta un răspuns fără sens și zgomotos, care este rostul acestui algoritm? Răspunsul este că ne permite să găsim un echilibru între utilitate și confidențialitate. Vrem ca publicul larg să obțină o anumită utilitate din baza noastră de date, fără a expune date sensibile unui posibil adversar.
Ce ar primi de fapt adversarul? Răspunsurile sunt raportate în tabelul 2.

Primul răspuns pe care adversarul îl primește este aproape de adevărul de bază, dar nu este egal cu acesta. În acest sens, adversarul este păcălit, este asigurată utilitatea și este protejată confidențialitatea. Dar, după mai multe încercări, acesta va fi capabil să estimeze adevărul de bază. Această „estimare din interogări repetate” este una dintre limitările fundamentale ale confidențialității diferențiale . Dacă adversarul poate efectua destule interogări la o bază de date cu confidențialitate diferențiată, acesta poate totuși să estimeze datele sensibile. Cu alte cuvinte, cu tot mai multe interogări, confidențialitatea este încălcată. Tabelul 2 demonstrează în mod empiric această încălcare a confidențialității. Cu toate acestea, după cum puteți vedea, intervalul de încredere de 90% din aceste 5 interogări este destul de larg; estimarea nu este încă foarte precisă.
Cât de precisă poate fi această estimare? Aruncați o privire la Figura 3, unde am rulat o simulare de mai multe ori și am trasat rezultatele .

Care linie verticală ilustrează lățimea unui interval de încredere de 95 %, iar punctele indică media datelor eșantionate de adversar. Rețineți că aceste diagrame au o axă orizontală logaritmică și că zgomotul este extras din variabile aleatoare Laplace independente și identic distribuite. În general, media este mai zgomotoasă cu mai puține interogări (deoarece dimensiunile eșantioanelor sunt mici). Așa cum era de așteptat, intervalele de încredere devin mai înguste pe măsură ce adversarul face mai multe interogări (deoarece mărimea eșantionului crește, iar zgomotul se reduce la zero). Doar din inspectarea graficului, putem vedea că este nevoie de aproximativ 50 de interogări pentru a face o estimare decentă.
Să reflectăm asupra acestui exemplu. În primul rând, prin adăugarea de zgomot aleatoriu, am făcut mai dificilă încălcarea confidențialității de către un adversar. În al doilea rând, strategia de ascundere pe care am folosit-o a fost simplu de implementat și de înțeles. Din nefericire, cu din ce în ce mai multe interogări, adversarul a fost capabil să aproximeze adevăratul număr.
Dacă mărim varianța zgomotului adăugat, ne putem apăra mai bine datele, dar nu putem adăuga pur și simplu orice zgomot Laplace la o funcție pe care dorim să o ascundem. Motivul este că cantitatea de zgomot pe care trebuie să o adăugăm depinde de sensibilitatea funcției, iar fiecare funcție are propria sa sensibilitate. În special, funcția de numărare are o sensibilitate de 1. Să analizăm ce înseamnă sensibilitatea în acest context.
Sensibilitatea și mecanismul Laplace
Pentru o funcție:
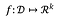
sensibilitatea lui f este:
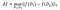
pe seturi de date D₁, D₂ care diferă în cel mult un element .
Definiția de mai sus este destul de matematică, dar nu este atât de rea pe cât pare. În linii mari, sensibilitatea unei funcții este cea mai mare diferență posibilă pe care un rând o poate avea asupra rezultatului funcției respective, pentru orice set de date. De exemplu, în setul nostru de date de jucărie, numărarea numărului de rânduri are o sensibilitate de 1, deoarece adăugarea sau eliminarea unui singur rând din orice set de date va modifica numărul cu cel mult 1.
Ca un alt exemplu, să presupunem că ne gândim la „număr rotunjit la un multiplu de 5”. Această funcție are o sensibilitate de 5 și putem arăta acest lucru destul de ușor. Dacă avem două seturi de date de mărime 10 și 11, acestea diferă într-un singur rând, dar „numărătorile rotunjite la un multiplu de 5” sunt 10 și respectiv 15. De fapt, cinci este cea mai mare diferență posibilă pe care o poate produce această funcție de exemplu. Prin urmare, sensibilitatea sa este 5.
Calcularea sensibilității pentru o funcție arbitrară este dificilă. O cantitate considerabilă de efort de cercetare este cheltuită pe estimarea sensibilităților , pe îmbunătățirea estimărilor sensibilității și pe ocolirea calculului sensibilității .
Cum se leagă sensibilitatea de numărarea zgomotoasă? Strategia noastră de numărare zgomotoasă a folosit un algoritm numit mecanismul Laplace, care, la rândul său, se bazează pe sensibilitatea funcției pe care o obscurizează . În Algoritmul 1, avem o implementare naivă în pseudocod a mecanismului Laplace .
Algoritmul 1
Intrare: Funcție F, intrare X, nivel de confidențialitate ϵ
Scoatere: Un răspuns zgomotos
Calculează F (X)
Calculează sensibilitatea lui F : S
Să extragă zgomotul L dintr-o distribuție Laplace cu varianța:
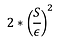
Întoarceți F(X) + L
Cu cât sensibilitatea S este mai mare, cu atât răspunsul va fi mai zgomotos. Numărătoarea are doar o sensibilitate de 1, deci nu trebuie să adăugăm mult zgomot pentru a păstra confidențialitatea.
Rețineți că mecanismul Laplace din Algoritmul 1 consumă un parametru epsilon. Ne vom referi la această cantitate ca fiind pierderea de confidențialitate a mecanismului și face parte din cea mai centrală definiție în domeniul confidențialității diferențiale: confidențialitatea diferențială epsilon. Pentru a ilustra, dacă ne amintim exemplul nostru anterior și folosim puțină algebră, putem vedea că mecanismul nostru de numărare zgomotoasă are o confidențialitate epsilon-diferențială, cu un epsilon de 0,707. Prin reglarea lui epsilon, controlăm caracterul zgomotos al numărătorii noastre zgomotoase. Alegerea unui epsilon mai mic produce rezultate mai zgomotoase și garanții de confidențialitate mai bune. Ca referință, Apple folosește un epsilon de 2 în autocorecția cu confidențialitate diferențială a tastaturii lor .
Cantitatea epsilon este modul în care confidențialitatea diferențială poate oferi comparații riguroase între diferite strategii. Definiția formală a confidențialității diferențiale epsilon este un pic mai implicată din punct de vedere matematic, așa că am omis-o intenționat din această postare pe blog. Puteți citi mai multe despre aceasta în studiul lui Dwork privind confidențialitatea diferențială .
După cum vă amintiți, exemplul de numărare zgomotoasă a avut un epsilon de 0,707, ceea ce este destul de mic. Dar tot am încălcat confidențialitatea după 50 de interogări. De ce? Pentru că, odată cu creșterea numărului de interogări, bugetul de confidențialitate crește și, prin urmare, garanția de confidențialitate este mai proastă.
Bugetul de confidențialitate
În general, pierderile de confidențialitate se acumulează. Atunci când două răspunsuri sunt returnate unui adversar, pierderea totală de confidențialitate este de două ori mai mare, iar garanția de confidențialitate este pe jumătate la fel de puternică. Această proprietate cumulativă este o consecință a teoremei de compoziție. În esență, cu fiecare nouă interogare, se eliberează informații suplimentare despre datele sensibile. Prin urmare, teorema compoziției are o viziune pesimistă și presupune cel mai rău scenariu: cu fiecare nou răspuns se produce aceeași cantitate de scurgeri de informații. Pentru garanții puternice de confidențialitate, dorim ca pierderea de confidențialitate să fie mică. Astfel, în exemplul nostru în care avem o pierdere de confidențialitate de treizeci și cinci (după 50 de interogări la mecanismul nostru de numărare zgomotoasă Laplace), garanția de confidențialitate corespunzătoare este fragilă.
Cum funcționează confidențialitatea diferențială dacă pierderea de confidențialitate crește atât de repede? Pentru a asigura o garanție de confidențialitate semnificativă, curatorii de date pot impune o pierdere maximă de confidențialitate. Dacă numărul de interogări depășește pragul, atunci garanția de confidențialitate devine prea slabă și curatorul încetează să mai răspundă la interogări. Pierderea maximă de confidențialitate se numește bugetul de confidențialitate . Ne putem gândi la fiecare interogare ca la o „cheltuială” de confidențialitate care implică o pierdere incrementală de confidențialitate. Strategia de utilizare a bugetelor, cheltuielilor și pierderilor este cunoscută în mod corespunzător sub numele de contabilizarea confidențialității .
Contorizarea confidențialității este o strategie eficientă pentru a calcula pierderea de confidențialitate după interogări multiple, dar poate încorpora în continuare teorema compoziției. După cum s-a menționat anterior, teorema compoziției presupune cel mai rău scenariu. Cu alte cuvinte, există alternative mai bune.
Deep Learning
Deep learning este un subdomeniu al învățării automate, care se referă la antrenarea rețelelor neuronale profunde (DNN) pentru a estima funcții necunoscute . (La un nivel înalt, o DNN este o secvență de transformări afine și neliniare care mapează un spațiu n-dimensional într-un spațiu m-dimensional). Aplicațiile sale sunt larg răspândite și nu este necesar să fie repetate aici. Vom explora în mod privat modul de antrenare a unei rețele neuronale profunde.
Rețelele neuronale profunde sunt antrenate de obicei folosind o variantă de coborâre stocastică a gradientului (SGD). Abadi et al. au inventat o versiune care păstrează confidențialitatea a acestui algoritm popular, denumită în mod obișnuit „SGD privat” (sau PSGD). Figura 4 ilustrează puterea în tehnica lor nouă . Abadi et al. au inventat o nouă abordare: contabilul de momente. Ideea de bază din spatele contabilului de momente este de a acumula cheltuielile de confidențialitate prin încadrarea pierderii de confidențialitate ca o variabilă aleatorie și utilizarea funcțiilor generatoare de momente pentru a înțelege mai bine distribuția acelei variabile (de unde și numele) . Detaliile tehnice complete sunt în afara scopului unei postări introductive pe blog, dar vă încurajăm să citiți lucrarea originală pentru a afla mai multe.

Gânduri finale
Am trecut în revistă teoria confidențialității diferențiale și am văzut cum poate fi folosită pentru a cuantifica confidențialitatea. Exemplele din această postare arată cum pot fi aplicate ideile fundamentale și legătura dintre aplicație și teorie. Este important să ne amintim că garanțiile de confidențialitate se deteriorează odată cu utilizarea repetată, așa că merită să ne gândim cum să atenuăm acest lucru, fie că este vorba de bugetarea confidențialității sau de alte strategii. Puteți investiga deteriorarea făcând clic pe această propoziție și repetând experimentele noastre. Există încă multe întrebări la care nu s-a răspuns aici și o multitudine de literatură de explorat – consultați referințele de mai jos. Vă încurajăm să citiți mai departe.
Cynthia Dwork. Confidențialitatea diferențială: A survey of results. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Laplace distribution, iulie 2018.
Aaruran Elamurugaiyan. Diagrame care demonstrează eroarea standard a răspunsurilor diferențiat private în funcție de numărul de interogări, august 2018.
Benjamin I. P. Rubinstein și Francesco Alda. Confidențialitate diferențială aleatorie fără durere cu eșantionare de sensibilitate. În 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork și Aaron Roth. The algorithmic foundations of differential privacy . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, și Li Zhang. Învățare profundă cu confidențialitate diferențială. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Interogări integrate de confidențialitate: An extensible platform for privacy-preserving data analysis. În Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, paginile 19-30, New York, NY, SUA, 2009. ACM.
Wikipedia Contributors. Deep Learning, august 2018.
.
Leave a Reply