O introducere delicată în problema corpului convex

Corpurile convexe tind să fie utile în multe domenii diferite, uneori chiar neașteptat. În acest articol, voi explica Ideea de bază a coifurilor convexe 2d și modul de utilizare a scanării graham pentru a le găsi. Deci, dacă știți deja despre scanarea graham, atunci acest articol nu este pentru dumneavoastră, dar dacă nu, acest lucru ar trebui să vă familiarizeze cu unele dintre conceptele relevante.

Cocoșul convex al unui set de puncte este definit ca fiind cel mai mic poligon convex, care cuprinde toate punctele din set. Convex înseamnă că poligonul nu are nici un colț îndoit spre interior.

Arginile roșii de pe poligonul din dreapta delimitează colțul în care forma este concavă, opusul celei convexe.

Un mod util de a ne gândi la coca convexă este analogia cu elasticul. Să presupunem că punctele din set sunt cuie, care ies dintr-o suprafață plană. Imaginați-vă acum, ce s-ar întâmpla dacă ați lua o bandă de cauciuc și ați întinde-o în jurul cuielor. Încercând să se contracte înapoi la lungimea sa inițială, elasticul ar înconjura cuiele, atingându-le pe cele care ies cel mai departe de centru.

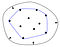
Pentru a reprezenta coca convexă rezultată în cod, de obicei stocăm lista punctelor care susțin această bandă elastică, adică lista punctelor de pe coca convexă.

Rețineți că mai trebuie să definim ce ar trebui să se întâmple dacă trei puncte se află pe aceeași dreaptă. Dacă vă imaginați că elasticul are un punct în care atinge unul dintre cuie, dar nu se îndoaie deloc acolo, înseamnă că acel cui de acolo se află pe o linie dreaptă între alte două cuie. În funcție de problemă, am putea considera că acest cui de-a lungul liniei drepte face parte din ieșire, deoarece atinge elasticul. Pe de altă parte, am putea spune, de asemenea, că acest cui nu ar trebui să facă parte din ieșire, deoarece forma elasticului nu se schimbă atunci când îl îndepărtăm. Această decizie depinde de problema la care lucrați în acel moment și, cel mai bine, dacă aveți o intrare în care niciunul dintre cele trei puncte nu este coliniar (acesta este adesea cazul în sarcinile ușoare pentru concursurile de programare), atunci puteți chiar să ignorați complet această problemă.

Căutarea coca convexă

Urmărind un set de puncte, intuiția umană ne permite să ne dăm seama rapid care puncte sunt susceptibile să atingă coca convexă și care dintre ele vor fi mai aproape de centru și, prin urmare, departe de coca convexă. Dar transpunerea acestei intuiții în cod necesită un pic de muncă.

Pentru a găsi coca convexă a unui set de puncte, putem folosi un algoritm numit Graham Scan, care este considerat a fi unul dintre primii algoritmi de geometrie computațională. Folosind acest algoritm, putem găsi subansamblul de puncte care se află pe coca convexă, împreună cu ordinea în care aceste puncte sunt întâlnite atunci când ne deplasăm în jurul coca convexă.

Algoritmul începe cu găsirea unui punct, despre care știm cu siguranță că se află pe coca convexă. Punctul cu cea mai mică coordonată y, de exemplu, poate fi considerat o alegere sigură. Dacă există mai multe puncte la aceeași coordonată y, îl luăm pe cel care are cea mai mare coordonată x (acest lucru funcționează și cu alte puncte de colț, de exemplu, mai întâi cel mai mic x, apoi cel mai mic y).

În continuare, sortăm celelalte puncte în funcție de unghiul la care se află, văzut din punctul de plecare. Dacă se întâmplă ca două puncte să se afle la același unghi, punctul care este mai aproape de punctul de plecare ar trebui să apară mai devreme în sortare.

Acum, ideea algoritmului este de a se plimba în jurul acestui tablou sortat, determinând pentru fiecare punct, dacă acesta se află sau nu pe coca convexă. Aceasta înseamnă că, pentru fiecare triplu de puncte pe care îl întâlnim, decidem dacă acestea formează un colț convex sau concav. Dacă colțul este concav, atunci știm că punctul din mijloc din acest triplet nu se poate afla pe coca convexă.

(Rețineți că termenii de colț concav și convex trebuie folosiți în raport cu întregul poligon, doar un colț de unul singur nu poate fi convex sau concav, deoarece nu ar exista o direcție de referință.)

Memorizăm punctele care se află pe coca convexă pe o stivă, în acest fel putem adăuga puncte dacă ajungem la ele pe drumul nostru în jurul punctelor sortate și le putem elimina dacă descoperim că formează un colț concav.

(Strict vorbind, trebuie să accesăm primele două puncte din stivă, de aceea folosim în schimb un std::vector, dar ne gândim la ea ca la un fel de stivă, pentru că întotdeauna suntem preocupați doar de primele două elemente.)

Întorcându-ne în jurul tabloului de puncte sortate, adăugăm punctul la stivă, iar dacă mai târziu descoperim că punctul nu aparține coca convexă, îl eliminăm.

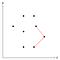
Potem măsura dacă colțul curent se curbează spre interior sau spre exterior calculând produsul încrucișat și verificând dacă acesta este pozitiv sau negativ. Figura de mai sus arată o tripletă de puncte în care colțul pe care îl formează este convex, prin urmare cel din mijloc dintre aceste trei puncte rămâne deocamdată pe stivă.

Prin urmare, trecând la următorul punct, continuăm să facem același lucru: verificăm dacă colțul este convex și dacă nu, eliminăm punctul. Apoi continuăm să adăugăm următorul punct și repetăm.

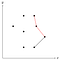
Acest colț marcat cu roșu este concav, prin urmare eliminăm punctul din mijloc din stivă, deoarece nu poate face parte din coca convexă.

Cum știm că acest lucru ne va da răspunsul corect?

Scrierea unei demonstrații riguroase iese din scopul acestui articol, dar pot să scriu ideile de bază. Vă încurajez, totuși, să mergeți mai departe și să încercați să completați lacunele!

Din moment ce am calculat produsul încrucișat la fiecare colț, știm cu siguranță că vom obține un poligon convex. Acum trebuie doar să demonstrăm, că acest poligon convex chiar înglobează toate punctele.

(De fapt, ar mai trebui să arătați că acesta este cel mai mic poligon convex posibil care satisface aceste condiții, dar acest lucru rezultă destul de ușor din faptul că punctele de colț ale poligonului nostru convex sunt un subset al setului inițial de puncte.)

Să presupunem că există un punct P în afara poligonului pe care tocmai l-am găsit.

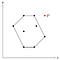
Din moment ce fiecare punct a fost adăugat în stivă o dată, știm că P a fost eliminat din stivă la un moment dat. Aceasta înseamnă că P, împreună cu punctele sale vecine, să le numim O și Q, au format un colț concav.

Din moment ce O și Q se află în interiorul poligonului (sau pe granița acestuia), P ar trebui să se afle și el în interiorul graniței, deoarece poligonul este convex, iar colțul pe care O și Q îl formează cu P este concav în raport cu poligonul.

Atunci am găsit o contradicție, ceea ce înseamnă că un astfel de punct P nu poate exista.

Implementare

Implementarea oferită aici are o funcție convex_hull, care ia un std::vector care conține punctele ca std::pairs de ints și returnează un alt std::vector care conține punctele care se află pe coca convexă.

Analiza timpului de execuție și a memoriei

Este întotdeauna util să ne gândim la algoritmii de complexitate în termeni de notație Big-O, pe care nu o voi explica aici, deoarece Michael Olorunnisola de aici a făcut deja o treabă mult mai bună de explicare decât aș face-o eu probabil:

Sortarea punctelor necesită inițial timp O(n log n), dar după aceea, fiecare pas poate fi calculat în timp constant. Fiecare punct este adăugat și eliminat din stivă cel mult o dată, ceea ce înseamnă că timpul de execuție în cel mai rău caz se situează în O(n log n).

Utilizarea memoriei, care în acest moment se situează în O(n), ar putea fi optimizată prin eliminarea necesității stivei și efectuarea operațiilor direct pe matricea de intrare. Am putea muta punctele care se află pe coca convexă la începutul matricei de intrare și să le aranjăm în ordinea corectă, iar celelalte puncte ar fi mutate în restul matricei. Funcția ar putea apoi să returneze doar o singură variabilă întreagă care denotă numărul de puncte din matrice care se află pe coca convexă. Bineînțeles, acest lucru are dezavantajul că funcția devine mult mai complicată și, prin urmare, v-aș sfătui să nu faceți acest lucru, cu excepția cazului în care codificați pentru sisteme încorporate sau aveți probleme de memorie la fel de restrictive. Pentru majoritatea situațiilor, compromisul probabilitate de eroare/economie de memorie pur și simplu nu merită.

Alți algoritmi

O alternativă la Graham Scan este algoritmul lui Chan, care se bazează efectiv pe aceeași idee, dar este mai ușor de implementat. Totuși, are sens să înțelegeți mai întâi cum funcționează Graham Scan.

Dacă vă simțiți cu adevărat fantezist și doriți să abordați problema în trei dimensiuni, aruncați o privire la algoritmul lui Preparata și Hong introdus în lucrarea lor din 1977 „Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.

.