Articles /

Matematică pentru arte liberale

Rezultatele învățării

  • Define și identifică autosimilaritatea în forme geometrice, plante, și formațiuni geologice
  • Generați o formă fractală având în vedere un inițiator și un generator
  • Dimensionați un obiect geometric cu un factor de scalare specific utilizând relația dimensiune de scalare
  • Determinați dimensiunea fractală a unui obiect fractal

În plus față de autosimilaritatea vizuală, fractalii prezintă și alte proprietăți interesante. De exemplu, observați că fiecare pas al iterației garniturii Sierpinski elimină un sfert din suprafața rămasă. Dacă acest proces este continuat la nesfârșit, am ajunge să eliminăm, în esență, toată suprafața, ceea ce înseamnă că am început cu o suprafață bidimensională și, cumva, ajungem cu ceva mai puțin decât atât, dar aparent mai mult decât o linie unidimensională.

Pentru a explora această idee, trebuie să discutăm despre dimensiune. Ceva precum o linie este 1-dimensională; are doar lungime. Orice curbă este 1-dimensională. Lucruri precum cutiile și cercurile sunt 2-dimensionale, deoarece au lungime și lățime, descriind o suprafață. Obiecte precum cutiile și cilindrii au lungime, lățime și înălțime, descriind un volum, și sunt 3-dimensionale.

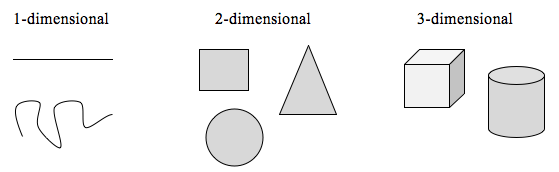
Obiectele 1-dimensionale includ o linie dreaptă și o linie ondulată neregulată. Obiectele bidimensionale includ un dreptunghi, un triunghi și un cerc. Obiectele tridimensionale includ un cub și un cilindru.

Se aplică anumite reguli pentru scalarea obiectelor, legate de dimensiunea lor.

Dacă aș avea o linie cu lungimea 1 și aș vrea să-i scalez lungimea cu 2, aș avea nevoie de două copii ale liniei originale. Dacă aș avea o linie cu lungimea 1 și aș vrea să-i scalez lungimea cu 3, aș avea nevoie de trei copii ale originalului.

1, o linie orizontală. 2, o linie orizontală de două ori mai lungă. 3, o linie orizontală de trei ori mai lungă.

Dacă aș avea un dreptunghi cu lungimea 2 și înălțimea 1, și aș vrea să-i scalez lungimea și lățimea cu 2, aș avea nevoie de patru copii ale dreptunghiului original. Dacă aș vrea să măresc lungimea și lățimea cu 3, aș avea nevoie de nouă exemplare ale dreptunghiului original.

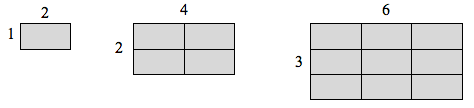
Un dreptunghi cu laturile măsurând 1 și 2. Apoi, patru copii ale acelui dreptunghi pentru a forma un dreptunghi mai mare cu laturile măsurând 2 și 4. Apoi, nouă copii ale primului dreptunghi pentru a forma un dreptunghi mai mare cu laturile măsurând 3 și 6.

Dacă aș avea o cutie cubică cu laturile de lungime 1 și aș vrea să-i măresc lungimea și lățimea cu 2, aș avea nevoie de opt copii ale cubului original. Dacă aș vrea să măresc lungimea și lățimea cu 3, aș avea nevoie de 27 de copii ale cubului original.

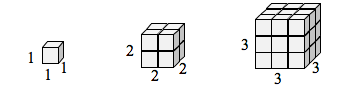
Un cub cu laturile măsurând 1 pe 1 pe 1 pe 1. Apoi, opt copii ale acelui cub pentru a forma un cub mai mare cu laturile măsurând 2 pe 2 pe 2. Apoi, 27 de copii ale cubului original pentru a forma un cub mai mare măsurând 3 pe 3 pe 3 pe 3.

Observați că, în cazul unidimensional, exemplarele necesare = scara.

În cazul bidimensional, exemplarele necesare = scara^{2}.

În cazul tridimensional, exemplarele necesare = scara^{3}.

Din aceste exemple, am putea deduce un model.

Relația scară-dimensiuni

Pentru a scala o formă D-dimensională cu un factor de scalare S, numărul de copii C necesare ale formei originale va fi dat de:

:

\text{Copii}=\text{Scale}^{\text{Dimensiune}}, sau C=S^{D}

Exemplu

Utilizați relația scară-dimensiune pentru a determina dimensiunea garniturii Sierpinski.

Să presupunem că definim garnitura originală ca având lungimea laturii 1. Garnitura mai mare prezentată este de două ori mai lată și de două ori mai înaltă, deci a fost redimensionată cu un factor 2.

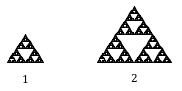
Galonul garnitura Sierpinski. În continuare, un triunghi mai mare alcătuit din trei triunghiuri de garnitură Sierpinski și un triunghi alb în centru.

Atenție, pentru a construi garnitura mai mare, sunt necesare 3 copii ale garniturii originale.

Utilizând relația scară-dimensiune C=S^{D}, obținem ecuația 3=2^{D}.

Din moment ce 2^{1}=2 și 2^{2}=4, putem vedea imediat că D este undeva între 1 și 2; garnitura este mai mult decât o formă 1-dimensională, dar am îndepărtat atât de multă suprafață încât acum este mai puțin decât 2-dimensională.

Soluționarea ecuației 3=2^{D} necesită logaritmi. Dacă ați studiat mai devreme logaritmii, este posibil să vă amintiți cum să rezolvați această ecuație (dacă nu, treceți la caseta de mai jos și folosiți această formulă cu tasta log de pe un calculator):

Tăiați logaritmul ambelor părți.

3={{2}^{D}}

Utilizați proprietatea exponentului logaritmilor.

\log(3)=\log\stânga({{2}^{D}}\dreapta)

Divizați cu log(2).

\log(3)=D\log\stânga(2\dreapta)

Dimensiunea garniturii este de aproximativ 1,585.

D=\frac{\log\stânga(3\dreapta)}{\log(2)}\aproximativx1.585

Relația scară-dimensiune, pentru a afla dimensiunea

Pentru a afla dimensiunea D a unui fractal, determinați factorul de scalare S și numărul de copii C ale formei originale necesare, apoi folosiți formula

D=\frac{\log\stânga(C\dreapta)}{\log(S)}

Încercați

Determinați dimensiunea fractală a fractalului produs cu ajutorul inițiatorului și al generatorului.

Inițiatorul este un pătrat. Generatorul este format din cinci pătrate care formează un model în formă de carouri.
Arată soluția

Dimensionarea fractalului cu un factor de 3 necesită 5 copii ale originalului.

D=\frac{\text{log}\stânga(5\dreapta)}{\text{log}\stânga(3\dreapta)}\aproximativx1,465

În următorul video, prezentăm un exemplu prelucrat de determinare a dimensiunii garniturii Sierpinski

.

Leave a Reply