Articles / ianuarie 22, 2022

Introducing Consistent Hashing

30 apr, 2020 – 11 min citește

Cu creșterea arhitecturilor distribuite, hashing-ul consistent a devenit majoritar. Dar ce este mai exact și în ce se deosebește de un algoritm standard de hashing? Care sunt motivațiile exacte care stau la baza acestuia?

În primul rând, vom descrie principalele concepte. Apoi, vom cerceta algoritmii existenți pentru a înțelege provocările asociate cu hashing-ul consistent.

Hashing

Hashing-ul este procesul de cartografiere a datelor de mărime arbitrară în valori de mărime fixă. Fiecare algoritm existent are propriile sale specificații:

MD5 produce valori hash pe 128 de biți.
SHA-1 produce valori hash pe 160 de biți.
etc.

Hashing-ul are multe aplicații în informatică. De exemplu, una dintre aceste aplicații se numește checksum. Pentru a verifica integritatea unui set de date este posibil să se utilizeze un algoritm de hashing. Un server realizează hash-ul unui set de date și indică valoarea hash unui client. Apoi, clientul își hașează versiunea sa a setului de date și compară valorile hash. Dacă acestea sunt egale, integritatea ar trebui să fie verificată.

„Ar trebui” aici este important. Cel mai rău scenariu este atunci când are loc o coliziune. O coliziune este atunci când două bucăți distincte de date au aceeași valoare hash. Să luăm un exemplu din viața reală prin definirea următoarei funcții de hashing: dată fiind o persoană, aceasta returnează data de naștere a acesteia (ziua & luna nașterii). Paradoxul zilei de naștere ne spune că, dacă avem doar 23 de persoane într-o cameră, probabilitatea ca două persoane să aibă aceeași zi de naștere (deci o coliziune) este mai mare de 50%. Prin urmare, funcția de zi de naștere nu este probabil o bună funcție de hashing.

Ca o introducere rapidă în hashing, este important să înțelegem că ideea principală se referă la răspândirea valorilor pe un domeniu. De exemplu:

MD5 răspândește valorile pe un domeniu spațial de 128 de biți
Un hashtable (sau hashmap) susținut de o matrice de 32 de elemente are o funcție hashing internă care răspândește valorile la orice index (de la 0 la 31).

Distribuția sarcinii

Distribuția sarcinii poate fi definită ca fiind procesul de răspândire a sarcinii între noduri. Termenul nod aici este interschimbabil cu server sau instanță. Este o unitate de calcul.

Balansarea sarcinii este un exemplu de distribuție a sarcinii. Este vorba despre distribuirea unui set de sarcini pe un set de resurse. De exemplu, folosim load balancing pentru a distribui cererile API între instanțele serverului web.

Când vine vorba de date, folosim mai degrabă termenul de sharding. Un shard de bază de date este o partiție orizontală a datelor dintr-o bază de date. Un exemplu tipic este o bază de date partiționată în trei shard-uri, unde fiecare shard are un subset din totalul datelor.

Load balancing și sharding au câteva provocări comune. Împărțirea uniformă a datelor, de exemplu, pentru a garanta că un nod nu este supraîncărcat în comparație cu celelalte. În anumite contexte, load balancing și sharding trebuie, de asemenea, să continue să asocieze sarcini sau date aceluiași nod:

Dacă avem nevoie să serializăm, să tratăm una câte una, operațiile pentru un anumit consumator, trebuie să direcționăm cererea către același nod.
Dacă avem nevoie să distribuim date, trebuie să știm care shard este proprietarul pentru o anumită cheie.

Vă sună familiar? În aceste două exemple, răspândim valorile pe un domeniu. Fie că este vorba de o sarcină răspândită în noduri de server sau de date răspândite în shardul bazei de date, regăsim ideea asociată cu hashing-ul. Acesta este motivul pentru care hashing-ul poate fi utilizat împreună cu distribuția sarcinii. Să vedem cum.

Mod-n Hashing

Principiul mod-n hashing este următorul. Fiecare cheie este hașurată folosind o funcție de hașurare pentru a transforma o intrare într-un număr întreg. Apoi, se efectuează un modulo bazat pe numărul de noduri.

Să vedem un exemplu concret cu 3 noduri. Aici, trebuie să distribuim sarcina între aceste noduri pe baza unui identificator de cheie. Fiecare cheie este hașurată, apoi efectuăm o operație modulo:

Beneficiul acestei abordări este lipsa de stateless. Nu trebuie să păstrăm nicio stare care să ne amintească faptul că foo a fost direcționat către nodul 2. Cu toate acestea, trebuie să știm câte noduri sunt configurate pentru a aplica operația modulo.

Apoi, cum funcționează mecanismul în cazul extinderii sau intrării în scară (adăugând sau eliminând noduri)? Dacă mai adăugăm încă un nod, operația modulo se bazează acum pe 4 în loc de 3:

După cum vedem, cheile foo și baz nu mai sunt asociate aceluiași nod. În cazul hashing-ului mod-n, nu există nicio garanție de menținere a consecvenței în asocierea cheie/nod. Este aceasta o problemă? S-ar putea.

Ce se întâmplă dacă implementăm un datastore folosind sharding și bazându-ne pe strategia mod-n pentru a distribui datele? Dacă scalăm numărul de noduri, trebuie să efectuăm o operațiune de rebalansare. În exemplul anterior, rebalansarea înseamnă:

Mutarea lui foo de la nodul 2 la nodul 0.
Mutarea lui baz de la nodul 2 la nodul 3.

Acum, ce se întâmplă dacă am fi stocat milioane sau chiar miliarde de date și că trebuie să rebalansăm aproape totul? După cum ne putem imagina, acesta ar fi un proces greoi. Prin urmare, trebuie să ne schimbăm tehnica de distribuție a încărcăturii pentru a ne asigura că la reechilibrare:

Distribuția rămâne cât mai uniformă posibil pe baza noului număr de noduri.
Numărul de chei pe care trebuie să le migrăm ar trebui să fie limitat. În mod ideal, ar fi doar 1/n la sută din chei, unde n este numărul de noduri.

Acesta este exact scopul algoritmilor de hashing consecvenți.

Termenul consecvent ar putea fi totuși oarecum confuz. Am întâlnit ingineri care presupuneau că astfel de algoritmi continuă să asocieze o anumită cheie exact aceluiași nod chiar și în fața scalabilității. Acest lucru nu este cazul. Trebuie să fie consecvent până la un anumit punct pentru a păstra distribuția uniformă.

Acum, este timpul să ne ocupăm de unele soluții.

Rendezvous

Rendezvous a fost primul algoritm propus vreodată pentru a rezolva problema noastră. Deși studiul original, publicat în 1996, nu a menționat termenul de hashing consistent, acesta oferă o soluție la provocările pe care le-am descris. Să vedem o posibilă implementare în Go:

Cum funcționează? Parcurgem fiecare nod și calculăm valoarea hash a acestuia. Valoarea hash este returnată de o funcție hash care produce un număr întreg pe baza unei chei (intrarea noastră) și a unui identificator de nod (cea mai simplă abordare este de a face hash concatenarea celor două șiruri de caractere). Apoi, returnăm nodul cu cea mai mare valoare hash. Acesta este motivul pentru care algoritmul este cunoscut și sub numele de hashing cu cea mai mare pondere aleatorie.

Principalul dezavantaj al rendezvous-ului este complexitatea sa în timp O(n), unde n este numărul de noduri. Este foarte eficient dacă avem nevoie de un număr limitat de noduri. Totuși, dacă începem să menținem mii de noduri, ar putea începe să cauzeze probleme de performanță.

Ring Consistent Hash

Următorul algoritm a fost lansat în 1997 de Karger et al. în această lucrare. Acest studiu a menționat pentru prima dată termenul de hashing consistent.

Se bazează pe un inel (o matrice conectată de la un capăt la altul). Deși este cel mai popular algoritm de hashing consistent (sau cel puțin cel mai cunoscut), principiul nu este întotdeauna bine înțeles. Să ne scufundăm în el.

Prima operație constă în crearea inelului. Un inel are o lungime fixă. În exemplul nostru, îl împărțim în 12 părți:

Apoi, ne poziționăm nodurile. În exemplul nostru vom defini N0, N1 și N2.

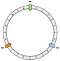
Nodurile sunt distribuite uniform deocamdată. Vom reveni asupra acestui punct mai târziu.

Apoi, este timpul să vedem cum să reprezentăm cheile. În primul rând, avem nevoie de o funcție f care returnează un indice inelar (de la 0 la 11) pe baza unei chei. Putem folosi hashing mod-n pentru asta. Deoarece lungimea inelului este constantă, aceasta nu ne va cauza nicio problemă.

În exemplul nostru vom defini 3 chei: a, b și c. Vom aplica f pe fiecare dintre ele. Să presupunem că avem următoarele rezultate:

f(a) = 1
f(a) = 5
f(a) = 7

Prin urmare, putem poziționa cheile pe inel în acest fel:

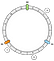
Cum asociem o anumită cheie unui nod? Principala logică este aceea de a merge înainte. De la o cheie dată, returnăm primul nod pe care îl găsim în continuare în timp ce progresăm înainte:

În acest exemplu, asociem a la N1, b și c la N2.

Acum, să vedem cum se gestionează reechilibrarea. Definim un alt nod N3. Unde ar trebui să îl poziționăm? Nu mai există spațiu pentru ca distribuția globală să fie uniformă. Ar trebui să reorganizăm nodurile? Nu, altfel nu am mai fi consecvenți, nu-i așa? Pentru a poziționa un nod, reutilizăm aceeași funcție de hașurare f pe care am introdus-o. În loc să fie apelată cu o cheie, ea poate fi apelată cu un identificator de nod. Astfel, poziția noului nod este decisă în mod aleatoriu.

Se ridică atunci o întrebare: ce ar trebui să facem cu a, deoarece următorul nod nu mai este N1:

Soluția este următoarea:

După cum am discutat anterior, un algoritm ideal ar trebui să reechilibreze în medie 1/n la sută din chei. În exemplul nostru, având în vedere că adăugăm un al patrulea nod, ar trebui să avem 25% din cheile posibile reasociate la N3. Este acesta cazul?

N0 de la indicii 8 la 12: 33,3% din totalul cheilor
N1 de la indicii 2 la 4: 16,6% din totalul cheilor
N2 de la indicii 4 la 8: 33.3% din totalul cheilor
N3 de la indicii 0 la 2: 16,6% din totalul cheilor

Distribuția nu este uniformă. Cum putem să o îmbunătățim? Soluția este să folosim noduri virtuale.

Să spunem că, în loc să poziționăm un singur punct pe nod, putem poziționa trei. De asemenea, trebuie să definim trei funcții de hashing diferite. Fiecare nod este hașurat de trei ori, astfel încât să obținem trei indici diferiți:

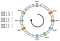
Potem aplica același algoritm prin deplasarea înainte. Cu toate acestea, o cheie ar fi asociată unui nod indiferent de nodul virtual pe care l-a întâlnit.

În chiar acest exemplu, distribuția ar fi acum următoarea:

N0: 33,3%
N1: 25%
N2: 41,6%

Cu cât mai multe noduri virtuale definim pentru fiecare nod, cu atât distribuția ar trebui să fie mai uniformă. În medie, cu 100 de noduri virtuale pe server, distribuția standard este de aproximativ 10%. Cu 1000, este de aproximativ 3,2%.

Acest mecanism este util și în cazul în care avem noduri cu dimensiuni diferite. De exemplu, dacă un nod este configurat să gestioneze teoretic o sarcină de două ori mai mare decât celelalte, am putea roti de două ori mai multe noduri virtuale.

Cu toate acestea, principalul dezavantaj al nodurilor virtuale este amprenta de memorie. Dacă trebuie să gestionăm mii de servere, ar fi nevoie de megaocteți de memorie.

Înainte de a trece mai departe, este interesant de remarcat că, uneori, un algoritm poate fi îmbunătățit substanțial prin schimbarea unei mici părți. Acesta este cazul, de exemplu, al unui algoritm publicat de Google în 2017 numit hashing consistent cu sarcini delimitate. Această versiune se bazează pe aceeași idee de inel pe care am descris-o noi. Cu toate acestea, abordarea lor este de a efectua o mică reechilibrare la orice actualizare (o nouă cheie sau un nou nod adăugat/eliminat). Această versiune o depășește pe cea originală în ceea ce privește abaterea standard, cu compromisul unei complexități temporale mai slabe.

Jump Consistent Hash

În 2007, doi ingineri de la Google au publicat jump consistent hash. În comparație cu algoritmul bazat pe inel, această implementare „nu necesită stocare, este mai rapidă și face o treabă mai bună în ceea ce privește împărțirea uniformă a spațiului de chei între găleți și împărțirea uniformă a volumului de lucru atunci când se schimbă numărul de găleți”. Spus altfel, îmbunătățește distribuția sarcinii de lucru între noduri (un bucket este același concept cu cel de nod) fără niciun fel de suprasolicitare a memoriei.

Iată algoritmul în C++ (7 linii de cod 🤯):

În hash consistent în inel, cu 1000 de noduri virtuale, abaterea standard a fost de aproximativ 3,2%. În jump consistent hash, nu mai avem nevoie de conceptul de noduri virtuale. Cu toate acestea, deviația standard rămâne mai mică de 0,0000001%.

Există totuși o limitare. Nodurile trebuie să fie numerotate secvențial. Dacă avem o listă de servere foo, bar și baz, nu putem elimina bar, de exemplu. Cu toate acestea, dacă configurăm un depozit de date, putem aplica algoritmul pentru a obține indexul shard pe baza numărului total de shards. Prin urmare, jump consistent hash poate fi util în contextul sharding-ului, dar nu și al load balancing-ului.

Ce este algoritmul Perfect Consistent Hashing?

Cum avem acum ceva experiență cu hashing-ul consistent, să facem un pas înapoi și să vedem care ar fi algoritmul perfect:

În medie, doar 1/n la sută din chei ar fi refăcute, unde n este numărul de noduri.
O complexitate spațială O(n) unde n este numărul de noduri.
O complexitate de timp O(1) pentru fiecare inserție/eliminare a unui nod și pentru fiecare căutare de chei.
O abatere standard minimă pentru a se asigura că un nod nu este supraîncărcat în comparație cu un altul.
Ar permite asocierea unei ponderi unui nod pentru a face față la dimensionarea diferită a nodurilor.
Ar permite denumirea arbitrară a nodurilor (fără a fi numerotate secvențial) pentru a susține atât echilibrarea sarcinii, cât și sharding.

Din păcate, acest algoritm nu există. Pe baza a ceea ce am văzut:

Rendezvous are o complexitate de timp liniară per căutare.
Ring consistent hash are o abatere standard minimă slabă fără conceptul de noduri virtuale. Cu noduri virtuale, este complexitatea spațială este O(n*v), cu n numărul de noduri și v numărul de noduri virtuale pe nod.
Jump consistent hash nu are o complexitate constantă în timp și nu suportă nume arbitrare de noduri.

Subiectul este încă deschis și există studii recente care merită analizate. De exemplu, hash-ul consistent cu mai multe sonde lansat în 2005. Acesta suportă o complexitate spațială O(1). Cu toate acestea, pentru a obține o abatere standard de ε, necesită un timp O(1/ε) pentru fiecare consultare. De exemplu, dacă dorim să obținem o abatere standard mai mică de 0,5%, este nevoie de o hashare a cheii de aproximativ 20 de ori. Prin urmare, putem obține o abatere standard minimă, dar cu efortul unei complexități mai mari a timpului de consultare.

După cum am spus în introducere, algoritmii de hashing consistent au devenit mainstream. Acum este utilizat în nenumărate sisteme, cum ar fi MongoDB, Cassandra, Riak, Akka etc., fie că este vorba de echilibrarea încărcăturii sau de distribuirea datelor. Cu toate acestea, ca de multe ori în știința informaticii, fiecare soluție are compromisuri.

Pe când vorbim despre compromisuri, dacă aveți nevoie de o continuare, poate doriți să aruncați o privire la excelenta postare scrisă de Damian Gryski:

Universe