Introducere în deconvoluție

Deconvoluția este o tehnică de procesare a imaginilor intensivă din punct de vedere computațional care este din ce în ce mai utilizată pentru îmbunătățirea contrastului și rezoluției imaginilor digitale capturate la microscop. Fundamentele se bazează pe o suită de metode care sunt concepute pentru a elimina sau inversa neclaritatea prezentă în imaginile de microscop indusă de deschiderea limitată a obiectivului.

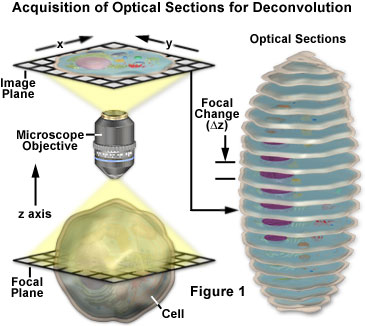
Chiar orice imagine achiziționată la un microscop digital cu fluorescență poate fi deconvoluită și sunt în curs de dezvoltare mai multe aplicații noi care aplică tehnici de deconvoluție la imaginile cu lumină transmisă colectate în cadrul unei varietăți de strategii de îmbunătățire a contrastului. Printre subiecții cei mai potriviți pentru îmbunătățirea prin deconvoluție se numără montajele tridimensionale construite dintr-o serie de secțiuni optice.

Conceptele de bază legate de achiziția de imagini în serie z pentru analiza deconvoluției sunt prezentate cu o diagramă schematică în figura 1. Se înregistrează o serie de imagini ale probei, fiecare fiind ușor decalată una față de cealaltă de-a lungul axei z. Această modificare a planului focal are ca rezultat o imagine ușor diferită, cu modificări subtile cauzate de lumina nefocalizată care provine de deasupra și de sub planul z curent. În timpul analizei de deconvoluție, întreaga serie z este analizată pentru a crea un set de date mai clare, cu o rezoluție mai mare, care nu este conturat de fluorescența în afara focalizării.

Deconvoluția este adesea sugerată ca o bună alternativă la microscopul confocal, deoarece ambele tehnici caută să minimizeze efectul fluorescenței în afara focalizării asupra imaginii finale. Acest lucru nu este strict adevărat, deoarece imaginile dobândite cu ajutorul unei deschideri de tip pinhole într-un microscop confocal beneficiază de procesarea deconvoluției. Microscopia confocală previne detectarea luminii nefocalizate prin plasarea unei deschideri de tip „pinhole” între obiectiv și detector, prin care pot trece doar razele de lumină focalizate. În schimb, microscoapele cu câmp larg permit ca lumina nefocalizată să treacă direct la detector. Deconvoluția se aplică apoi imaginilor rezultate, fie pentru a sustrage lumina nefocalizată, fie pentru a o reatribui înapoi la sursa sa. Microscopia confocală este deosebit de potrivită pentru examinarea specimenelor groase, cum ar fi embrionii sau testiculele, în timp ce procesarea deconvoluției widefield s-a dovedit a fi un instrument puternic pentru imagistica specimenelor care necesită niveluri de lumină extrem de scăzute. Aceste instrumente pot fi chiar combinate pentru a reduce zgomotul din imaginile achiziționate la un microscop confocal. Cu toate acestea, majoritatea experimentelor de deconvoluție raportate în literatura de specialitate se aplică imaginilor înregistrate pe un microscop de fluorescență standard cu câmp larg.

Sursele de degradare a imaginii

Degradarea imaginii poate fi împărțită în patru surse independente: zgomot, dispersie, strălucire și neclaritate. Figura 2 prezintă exemple de impact vizual al fiecăreia dintre acestea asupra aceleiași imagini.

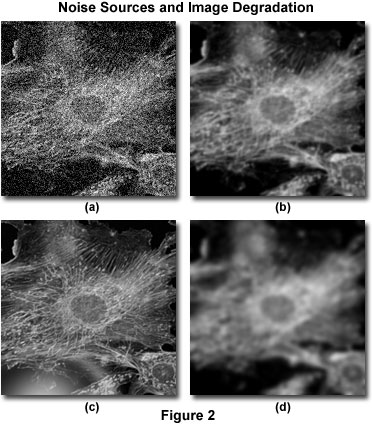
Zgomotul poate fi descris ca o dezorganizare cvasi-aleatorie a detaliilor dintr-o imagine, care (în forma sa cea mai severă) are aspectul de zgomot alb sau zgomot de sare și piper, similar cu ceea ce se observă la televiziunea audiovizuală atunci când se confruntă cu o recepție proastă [figura 2(a)]. Acest tip de zgomot este denumit „cvasi-aleatoriu”, deoarece distribuția statistică poate fi prezisă dacă se cunoaște mecanismul sursei. În microscopia digitală, principala sursă de zgomot este fie semnalul în sine (adesea denumit zgomot de fotografiere a fotonilor), fie sistemul de imagistică digitală. Mecanica ambelor surse de zgomot este înțeleasă și, prin urmare, distribuția statistică a zgomotului este cunoscută. Zgomotul dependent de semnal poate fi caracterizat de o distribuție Poisson, în timp ce zgomotul provenit de la sistemul de imagistică urmează adesea o distribuție gaussiană. Deoarece sursa și distribuția zgomotului comun în imaginile digitale este atât de bine înțeleasă, acesta poate fi eliminat cu ușurință prin aplicarea filtrelor de imagine adecvate, care sunt de obicei incluse în majoritatea pachetelor software de deconvoluție ca o rutină opțională de „preprocesare”.

Dispersia este de obicei menționată ca fiind o perturbare aleatorie a luminii indusă de modificările indicelui de refracție în cadrul unui specimen. Efectul net al dispersiei este o dezorganizare cu adevărat aleatorie a detaliilor imaginii, așa cum se manifestă în figura 2(b). Deși nu a fost elaborată o metodă complet satisfăcătoare pentru a prezice dispersia într-un anumit specimen, s-a demonstrat că gradul de dispersie depinde în mare măsură de grosimea specimenului și de proprietățile optice ale specimenului și ale materialelor de încorporare din jur. Dispersia crește atât cu grosimea specimenului, cât și cu eterogenitatea indicelui de refracție prezentat de componentele interne ale unui specimen.

Similară cu dispersia, strălucirea este o perturbare aleatorie a luminii, dar apare în elementele optice (lentile, filtre, prisme etc.) ale microscopului și nu în interiorul specimenului. Nivelul de strălucire într-un microscop modern a fost redus la minimum prin utilizarea lentilelor și a filtrelor cu acoperiri antireflectorizante și prin perfecționarea tehnicilor de formare a lentilelor, a cimenturilor optice și a formulărilor sticlei. Figura 2(c) ilustrează efectul strălucirii necontrolate.

Blur este descris de o răspândire nealeatorie a luminii care apare prin trecerea prin calea optică a sistemului de imagistică [Figura 2(d)]. Cea mai semnificativă sursă de neclaritate este difracția, iar o imagine a cărei rezoluție este limitată doar de neclaritate este considerată a fi limitată de difracție. Aceasta reprezintă o limită intrinsecă a oricărui sistem de imagistică și este factorul determinant în evaluarea limitei de rezoluție a unui sistem optic. Din fericire, sunt disponibile modele sofisticate de neclaritate într-un microscop optic, care pot fi utilizate pentru a determina sursa fotonilor defocalizați. Aceasta este baza pentru deconvoluție. Datorită importanței sale fundamentale în deconvoluție, modelul teoretic pentru neclaritate va fi discutat mult mai detaliat în alte părți ale acestei secțiuni. Cu toate acestea, trebuie subliniat faptul că toate sistemele de imagistică produc neclaritate independent de alte forme de degradare a imaginii induse de specimen sau de componentele electronice instrumentale însoțitoare. Tocmai această independență a neclarității optice față de alte tipuri de degradare este cea care permite posibilitatea eliminării neclarității prin tehnici de deconvoluție.

Interacțiunea luminii cu materia este originea fizică primară a împrăștierii, a strălucirii și a neclarității. Cu toate acestea, compoziția și aranjamentul moleculelor dintr-un anumit material (fie că este vorba de sticlă, apă sau proteine) conferă fiecărui material propriul set particular de proprietăți optice. În scopul deconvoluției, ceea ce distinge împrăștierea, strălucirea și neclaritatea sunt locul în care acestea apar și posibilitatea de a genera un model matematic pentru aceste fenomene. Deoarece împrăștierea este un fenomen localizat și neregulat care apare în specimen, s-a dovedit dificil de modelat. În schimb, deoarece neclaritatea este o funcție a sistemului optic al microscopului (în principal a obiectivului), aceasta poate fi modelată cu o relativă simplitate. Un astfel de model face posibilă inversarea matematică a procesului de încețoșare, iar deconvoluția utilizează acest model pentru a inversa sau a elimina încețoșarea.

Funcția de împrăștiere a punctului

Modelul pentru încețoșare care a evoluat în optica teoretică se bazează pe conceptul de funcție de împrăștiere a punctului (PSF) tridimensională. Acest concept este de o importanță fundamentală pentru deconvoluție și ar trebui să fie clar înțeles pentru a evita artefactele de imagine. Funcția de împrăștiere a punctului se bazează pe o sursă punctiformă infinit de mică de lumină care își are originea în spațiul specimenului (obiect). Deoarece sistemul de imagistică al microscopului colectează doar o fracțiune din lumina emisă de acest punct, acesta nu poate concentra lumina într-o imagine tridimensională perfectă a punctului. În schimb, punctul apare lărgit și răspândit într-un model de difracție tridimensional. Astfel, funcția de împrăștiere a punctului este definită în mod formal ca fiind modelul de difracție tridimensional generat de o sursă de lumină punctiformă ideală.

În funcție de modul de imagistică utilizat (câmp larg, confocal, lumină transmisă), funcția de împrăștiere a punctului are o formă și un contur diferit și unic. La un microscop de fluorescență cu câmp larg, forma funcției de împrăștiere a punctului seamănă cu cea a unei „mingi de fotbal” alungite de lumină înconjurată de o flacără de inele care se lărgesc. Pentru a descrie funcția de împrăștiere a punctului în trei dimensiuni, se obișnuiește să se aplice un sistem de coordonate cu trei axe (x, y și z), unde × și y sunt paralele cu planul focal al specimenului, iar z este paralel cu axa optică a microscopului. În acest caz, funcția de împrăștiere a punctelor apare ca un set de inele concentrice în planul x-y și seamănă cu o clepsidră în planurile x-z și y-z (așa cum este ilustrat în figura 3). O tăietură x-y prin centrul funcției de împrăștiere a punctelor în câmp larg dezvăluie un set de inele concentrice: așa-numitul disc Airy la care se face referire în mod obișnuit în textele despre microscopia optică clasică.

Două proiecții x-z ale funcțiilor de împrăștiere a punctelor care prezintă diferite grade de aberație sferică sunt prezentate în figura 3. Axa optică este paralelă cu axa verticală a imaginii. Funcția de împrăștiere a punctelor din stânga prezintă o aberație sferică minimă, în timp ce cea din dreapta prezintă un grad semnificativ de aberație. Rețineți că asimetria axială și lărgirea nodului central de-a lungul axei optice în imaginea din dreapta duce la o rezoluție axială degradată și la estomparea semnalului. În teorie, dimensiunea funcției de împrăștiere a punctului este infinită, iar intensitatea totală însumată a luminii în planurile îndepărtate de focar este egală cu intensitatea însumată la focar. Cu toate acestea, intensitatea luminii scade rapid și, în cele din urmă, devine imposibil de distins de zgomot. Într-o funcție de împrăștiere a punctului neaberată înregistrată cu un obiectiv cu imersie în ulei cu deschidere numerică mare (1,40), lumina care ocupă 0,2 micrometri pătrați în planul de focalizare este împrăștiată pe o suprafață de 90 de ori mai mare de 1 micrometru deasupra și sub focalizare. Specimenul utilizat pentru a înregistra aceste imagini ale funcției de împrăștiere a punctelor a fost o bilă fluorescentă cu diametrul de 0,1 micrometru montată în glicerol (indice de refracție egal cu 1,47), uleiurile de imersie având indicii de refracție notați în figură.

Un aspect important este modul în care funcția de împrăștiere a punctelor afectează formarea imaginii în microscop. Modelul teoretic de formare a imaginii tratează funcția de răspândire a punctului ca unitate de bază a unei imagini. Cu alte cuvinte, funcția de împrăștiere a punctelor este pentru imagine ceea ce este cărămida pentru casă. Cea mai bună imagine care poate fi vreodată este un ansamblu de funcții de împrăștiere a punctelor, iar creșterea măririi nu va schimba acest fapt. După cum explică un manual de optică teoretică de renume (Born and Wolf: Principles of Optics), „Este imposibil să se scoată în evidență detalii care nu sunt prezente în imaginea primară prin creșterea puterii ocularului, deoarece fiecare element al imaginii primare este un mic model de difracție, iar imaginea reală, așa cum este văzută de ocular, este doar ansamblul imaginilor mărite ale acestor modele”.

Ca exemplu, să luăm în considerare o populație de bile fluorescente cu rezoluție redusă, plasate între o lamelă de acoperire și o lamă de microscop. O imagine focalizată a acestui specimen dezvăluie un nor de puncte, care este de fapt un disc înconjurat de un mic set de inele (de fapt, un disc Airy; a se vedea figura 4(a)). Dacă acest specimen este ușor îndepărtat de la focalizare, un set mai mare de inele concentrice va apărea în locul în care se afla fiecare punct în imaginea focalizată (figura 4(b)). Atunci când se colectează o imagine tridimensională a acestui specimen, atunci se înregistrează o funcție completă de răspândire a punctelor pentru fiecare bulină. Funcția de împrăștiere a punctului descrie ceea ce se întâmplă cu fiecare sursă punctiformă de lumină după ce trece prin sistemul de imagistică.

Procesul de estompare tocmai descris este modelat matematic ca o convoluție. Operația de convoluție descrie aplicarea funcției de împrăștiere a punctelor în fiecare punct al specimenului: lumina emisă de fiecare punct al obiectului este convolată cu funcția de împrăștiere a punctelor pentru a produce imaginea finală. Din păcate, această convoluție face ca punctele din specimen să devină regiuni neclare în imagine. Luminozitatea fiecărui punct din imagine este legată liniar prin operația de convoluție de fluorescența fiecărui punct din specimen. Deoarece funcția de răspândire a punctului este tridimensională, neclaritatea din funcția de răspândire a punctului este un fenomen intrinsec tridimensional. Imaginea din orice plan focal conține lumină încețoșată de la punctele situate în acel plan, amestecată cu lumină încețoșată de la punctele provenite din alte planuri focale.

Situația poate fi rezumată cu ideea că imaginea este formată de o convoluție a specimenului cu funcția de împrăștiere a punctelor. Deconvoluția inversează acest proces și încearcă să reconstruiască specimenul dintr-o imagine neclară.

Aberrații în funcția de împrăștiere a punctelor

Funcția de împrăștiere a punctelor poate fi definită fie teoretic prin utilizarea unui model matematic de difracție, fie empiric prin achiziția unei imagini tridimensionale a unei bile fluorescente (a se vedea figura 3). O funcție teoretică de răspândire a punctului are, în general, simetrie axială și radială. De fapt, funcția de răspândire a punctului este simetrică deasupra și dedesubtul planului x-y (simetrie axială) și în rotație în jurul axei z (simetrie radială). O funcție empirică de răspândire a punctelor se poate abate semnificativ de la simetria perfectă (așa cum este prezentată în figura 3). Această deviație, denumită mai frecvent aberație, este produsă de neregularitățile sau nealinierile oricărei componente a trenului optic al sistemului de formare a imaginii, în special obiectivul, dar poate apărea și în cazul altor componente, cum ar fi oglinzile, separatoarele de fascicule, lentilele tubulare, filtrele, diafragmele și deschiderile. Cu cât calitatea componentelor optice este mai ridicată și cu cât alinierea microscopului este mai bună, cu atât funcția empirică de împrăștiere a punctelor se apropie mai mult de forma sa simetrică ideală. Atât microscopia confocală, cât și cea de deconvoluție depind de faptul că funcția de împrăștiere a punctului este cât mai aproape de cazul ideal.

Cea mai frecventă aberație întâlnită în microscopia optică, bine cunoscută de orice microscopist experimentat și profesionist, este aberația sferică. Manifestarea acestei aberații este o asimetrie axială în forma funcției de împrăștiere a punctelor, cu o creștere corespunzătoare a dimensiunii, în special de-a lungul axei z (figura 3). Rezultatul este o pierdere considerabilă a rezoluției și a intensității semnalului. În practică, sursa tipică de aberație sferică este o nepotrivire între indicii de refracție ai mediului de imersie al lentilei frontale a obiectivului și mediul de montaj în care este scăldat specimenul. Ar trebui să se pună un accent deosebit pe importanța reducerii la minimum a acestei aberații. Deși deconvoluția poate restabili parțial rezoluția pierdută, nicio cantitate de procesare a imaginii nu poate restabili semnalul pierdut.

.