Gibbs Sampling

Ca și alte metode MCMC, eșantionatorul Gibbs construiește un lanț Markov ale cărui valori converg către o distribuție țintă. Eșantionarea Gibbs este, de fapt, un caz specific al algoritmului Metropolis-Hastings în care propunerile sunt întotdeauna acceptate.

Pentru a detalia, să presupunem că doriți să eșantionați o distribuție de probabilitate multivariată.

Nota: O distribuție de probabilitate multivariată este o funcție de mai multe variabile (i.e. distribuție normală bidimensională).

Nu știm cum să eșantionăm direct din aceasta din urmă. Cu toate acestea, datorită unor conveniențe matematice sau poate pur și simplu norocului, se întâmplă să cunoaștem probabilitățile condiționate.

Aici intervine eșantionarea Gibbs. Eșantionarea Gibbs se aplică atunci când distribuția comună nu este cunoscută în mod explicit sau este dificil de eșantionat direct, dar distribuția condiționată a fiecărei variabile este cunoscută și este mai ușor de eșantionat.

Începem prin a selecta o valoare inițială pentru variabilele aleatoare X & Y. Apoi, eșantionăm din distribuția de probabilitate condiționată a lui X dat fiind Y = Y⁰ notată p(X|Y⁰). În etapa următoare, eșantionăm o nouă valoare a lui Y condiționată de X¹, pe care tocmai am calculat-o. Repetăm procedura pentru încă n – 1 iterații, alternând între extragerea unui nou eșantion din distribuția de probabilitate condiționată a lui X și din distribuția de probabilitate condiționată a lui Y, dată fiind valoarea curentă a celeilalte variabile aleatoare.

Să analizăm un exemplu. Să presupunem că avem următoarele distribuții de probabilitate posterioare și condiționate.

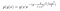
unde g(y) conține termenii care nu includ x, iar g(x) îi conține pe cei care nu depind de y.

Nu cunoaștem valoarea lui C (constanta de normalizare). Cu toate acestea, cunoaștem distribuțiile de probabilitate condiționate. Prin urmare, putem folosi eșantionarea Gibbs pentru a aproxima distribuția posterioară.

Nota: probabilitățile condiționate sunt de fapt distribuții normale și pot fi rescrise după cum urmează:

Date fiind ecuațiile precedente, vom trece la implementarea algoritmului de eșantionare Gibbs în Python. Pentru a începe, importăm următoarele biblioteci.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Definim funcția pentru distribuția posterioară (presupunem C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

După aceea, reprezentăm grafic distribuția de probabilitate.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Acum, vom încerca să estimăm distribuția de probabilitate folosind Gibbs Sampling. După cum am menționat anterior, probabilitățile condiționate sunt distribuții normale. Prin urmare, le putem exprima în termeni de mu și sigma.

În următorul bloc de cod, definim funcții pentru mu și sigma, inițializăm variabilele noastre aleatoare X & Y și stabilim N (numărul de iterații).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Pasăm prin algoritmul de eșantionare Gibbs.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

În cele din urmă, reprezentăm grafic rezultatele.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Cum se vede, distribuția de probabilitate obținută cu ajutorul algoritmului Gibbs Sampling face o treabă bună de aproximare a distribuției țintă.

Concluzie

Eșantionarea Gibbs este o metodă Monte Carlo în lanț Markov care extrage iterativ o instanță din distribuția fiecărei variabile, condiționată de valorile curente ale celorlalte variabile, pentru a estima distribuții comune complexe. Spre deosebire de algoritmul Metropolis-Hastings, se acceptă întotdeauna propunerea. Astfel, eșantionarea Gibbs poate fi mult mai eficientă.

.