Funcția lui Green

În general vorbind, o funcție Green este un nucleu integral care poate fi utilizat pentru a rezolva ecuații diferențiale dintr-un număr mare de familii, inclusiv exemple mai simple, cum ar fi ecuațiile diferențiale ordinare cu condiții de valoare inițială sau la limită, precum și exemple mai dificile, cum ar fi ecuațiile diferențiale parțiale (PDE) neomogene cu condiții la limită. Importante din mai multe motive, funcțiile lui Green permit interpretări vizuale ale acțiunilor asociate unei surse de forță sau unei sarcini concentrate într-un punct (Qin 2014), ceea ce le face deosebit de utile în domenii ale matematicii aplicate. În special, metodele funcțiilor lui Green sunt utilizate pe scară largă în, de ex, fizică și inginerie.

Mai precis, dat fiind un operator diferențial liniar care acționează asupra colecției de distribuții pe un subset al unui spațiu euclidian , o funcție Green în punctul corespunzător lui este orice soluție a

(1)

unde reprezintă funcția delta. Motivația pentru definirea unei astfel de funcții este larg răspândită, dar înmulțind identitatea de mai sus cu o funcție și integrând în raport cu se obține

(2)

Latura din dreapta se reduce pur și simplu la datorită proprietăților funcției delta, și deoarece este un operator liniar care acționează numai asupra lui și nu asupra lui , partea stângă poate fi rescrisă ca

(3)

Această reducere este deosebit de utilă atunci când se rezolvă pentru în ecuații diferențiale de forma

(4)

unde aritmetica de mai sus confirmă că

(5)

și de unde rezultă că are forma integrală specifică

(6)

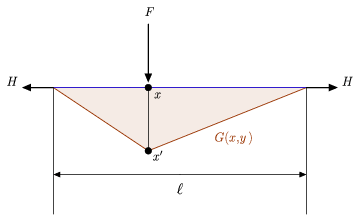
Figura de mai sus ilustrează atât interpretarea fizică intuitivă a unei funcții Green, cât și o ecuație diferențială asociată relativ simplă cu care se poate compara definiția de mai sus (Hartmann 2013). În special, aceasta arată o frânghie întinsă de lungime suspendată între doi pereți, menținută în poziție de o forță orizontală identică aplicată la fiecare dintre capetele sale și o sarcină laterală plasată într-un punct interior de pe frânghie. Fie punctul corespunzător lui de pe frânghia deformată, să presupunem că forța descendentă este constantă, să zicem , iar să denote deformarea frânghiei. Acestui sistem fizic îi corespunde ecuația diferențială

(7)

pentru cu , un sistem a cărui simplitate permite scrierea explicită atât a soluției sale , cât și a funcției sale Green :

(8)

și

(9)

respectiv. După cum se demonstrează în figura de mai sus, frânghia deplasată are formatul liniar pe bucățele dat de de mai sus, confirmând astfel afirmația că funcția lui Green asociată acestui sistem reprezintă acțiunea frânghiei orizontale corespunzătoare aplicării unei forțe .

O funcție Green care ia o pereche de argumente este denumită uneori funcție Green în două puncte. Aceasta este în contrast cu funcțiile Green cu mai multe puncte, care au o importanță deosebită în domeniul teoriei cu multe corpuri.

Ca exemplu elementar al unei funcții în două puncte, așa cum a fost definită mai sus, considerăm problema determinării potențialului generat de o distribuție de sarcină a cărei densitate de sarcină este , prin care aplicând ecuația lui Poisson și legea lui Coulomb la potențialul la produs de fiecare element de sarcină se obține o soluție

(10)

care este valabil, în anumite condiții, în regiunea în care . Deoarece partea dreaptă poate fi privită ca un operator integral care convertește în , se poate rescrie această soluție în termenii unei funcții Green având forma

(11)

în care soluția poate fi rescrisă:

(12)

(Arfken 2012).

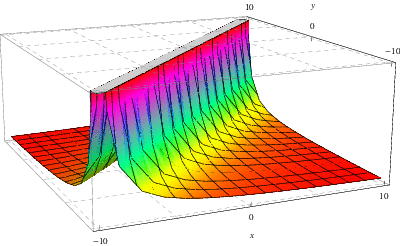
Figura de mai sus prezintă funcția Green asociată soluției ecuației – discutate mai sus unde aici, și , respectiv , este reprezentată pe axa -, respectiv -.

O listă oarecum cuprinzătoare a funcțiilor lui Green corespunzătoare diferitelor ecuații diferențiale este menținută online de Kevin Cole (Cole 2000).

Datorită multitudinii de literatură scrisă despre funcțiile lui Green, pot apărea mai multe notații și definiții diferite, dintre care unele sunt diferite din punct de vedere topic față de cele de mai sus, dar care în general nu afectează proprietățile importante ale rezultatelor. Așa cum ilustrează exemplul de mai sus, de exemplu, unii autori preferă să noteze variabilele și în termenii vectorilor și pentru a sublinia faptul că acestea sunt elemente ale lui pentru un oarecare care poate fi mai mare decât 1 (Arfken 1985). De asemenea, este relativ frecventă întâlnirea definiției cu semnul negativ, astfel încât este definită ca fiind funcția pentru care

(13)

dar, datorită faptului că această considerație pur fizică nu are niciun efect asupra matematicii de bază, acest punct de vedere este în general ignorat. Sunt cunoscute și alte câteva notații pentru funcția lui Green, dintre care unele includ utilizarea literei minuscule în loc de (Stakgold 1979), precum și includerea unei linii verticale în loc de virgulă, de exemplu: în loc de (Stakgold 1979), precum și includerea unei linii verticale în loc de virgulă, de ex, (Duffy 2001).

În alte cazuri, literatura de specialitate prezintă definiții care sunt strâns legate de contextele în care sunt prezentate. De exemplu, unii autori definesc funcțiile Green ca fiind funcții care satisfac un anumit set de condiții, de exemplu,existența pe un tip special de domeniu, asocierea cu un operator diferențial foarte particular , sau satisfacerea unui set precis de condiții la limită. Unul dintre cele mai frecvente astfel de exemple poate fi găsit în notele lui, de ex, Speck, în care o funcție Green este definită pentru a satisface pentru punctele și pentru toate punctele situate în limita a (Speck 2011). Această definiție particulară prezintă un nucleu integral corespunzător soluției unei ecuații Poisson generalizate și, prin urmare, s-ar confrunta cu limitări evidente atunci când ar fi adaptată la un cadru mai general. Pe de altă parte, astfel de exemple nu sunt lipsite de avantaje. În cazul exemplului Poisson generalizat de mai sus, de exemplu, fiecare astfel de funcție a lui Green poate fi divizată astfel încât

(14)

unde și pentru Laplacianul regulat (Hartman 2013). În astfel de situații, este cunoscută ca fiind soluția fundamentală a ecuației diferențiale subiacente, iar este cunoscută ca fiind soluția sa regulată; ca atare, și sunt uneori numite părțile fundamentală și, respectiv, regulată ale lui .

Câteva proprietăți fundamentale ale unei funcții Green generale rezultă imediat (sau aproape) din definiția sa și se transferă la toate cazurile particulare. De exemplu, dacă nucleul operatorului este netrivial, atunci pot exista mai multe funcții Green asociate unui singur operator; ca urmare, trebuie să se dea dovadă de prudență atunci când se face referire la „funcția Green”. Funcțiile lui Green satisfac o simetrie adiacentă în cele două argumente ale lor, astfel încât

(15)

unde aici, este definită ca fiind soluția ecuației

(16)

Aici, este adjunctul lui . Un corolar imediat al acestui fapt este că pentru operatorii autoadjuncți , este simetric:

(17)

Această identitate este adesea numită principiul reciprocității și spune, în termeni fizici, că răspunsul la cauzat de o sursă unitară la este același cu răspunsul la datorat unei forțe unitare la (Stakgold 1979).

Proprietatea esențială a oricărei funcții Green este aceea că oferă o modalitate de a descrie răspunsul unei soluții arbitrare de ecuație diferențială la un anumit tip de termen sursă în prezența unui anumit număr de condiții la limită (Arfken et al. 2012). Unii autori consideră că o funcție Green are în teoria ecuațiilor diferențiale parțiale un rol aproximativ analog cu cel al seriilor Fourier în rezolvarea ecuațiilor diferențiale ordinare (Mikula și Kos 2006).

Pentru scenarii mai abstracte, există o serie de concepte care servesc drept analogii specifice contextului la noțiunea de funcție Green. De exemplu, în analiza funcțională, este adesea util să se ia în considerare o așa-numită funcție Green generalizată, care are multe proprietăți analoge atunci când este integrată în mod abstract față de funcționale mai degrabă decât față de funcții. Într-adevăr, astfel de generalizări au dat naștere unei ramuri complet analoge a analizei teoretice a PDE și sunt ele însele în centrul unei mari cantități de cercetare.

.