Ce este geometria analitică?
Ce este geometria analitică?
Geometria analitică este o ramură a algebrei care este folosită pentru a modela obiecte geometrice – punctele, liniile (drepte) și cercurile fiind cele mai elementare dintre acestea. Geometria analitică este o mare invenție a lui Descartes și Fermat.
În geometria analitică plană, punctele sunt definite ca perechi ordonate de numere, de exemplu, (x, y), în timp ce dreptele sunt la rândul lor definite ca seturi de puncte care satisfac ecuații liniare, a se vedea expunerile excelente ale lui D. Pedoe sau D. Brannan et al. Din punctul de vedere al geometriei analitice, axiomele geometrice sunt teoreme derivabile. De exemplu, pentru orice două puncte distincte (x1, y1) și (x2, y2), există o singură dreaptă ax + by + c = 0 care trece prin aceste puncte. Coeficienții săi a, b, c pot fi găsiți (până la un factor constant) din sistemul liniar de două ecuații
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
sau direct din ecuația determinantului
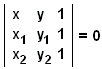 |
Cu toate acestea, nicio teorie axiomatică nu poate scăpa folosind elemente nedefinite. În teoria seturilor care stă la baza unei mari părți a matematicii și, în special, a geometriei analitice, cea mai fundamentală noțiune de set rămâne nedefinită.
Geometria spațiului tridimensional este modelată cu triple de numere (x, y, z) și o ecuație liniară 3D ax + by + cz + d = 0 definește un plan. În general, geometria analitică oferă un instrument convenabil pentru lucrul în dimensiuni superioare.
În cadrul geometriei analitice se pot modela (și se modelează) și geometrii neeuclidiene. De exemplu, în geometria proiectivă plană, un punct este o triplă de coordonate omogene (x, y, z), nu toate 0, astfel încât
| (tx, ty, tz) = (x, y, z), |
pentru tot t ≠ 0, în timp ce o dreaptă este descrisă de o ecuație omogenă
| ax + bx + cz = 0. |
În geometria analitică, secțiunile conice sunt definite prin ecuații de gradul al doilea:
| ax² + bxy + cy² + dx + ey + f = 0. |
Acea parte a geometriei analitice care se ocupă în principal cu ecuații liniare se numește Algebră liniară.
Geometria analitică carteziană este geometria în care axele x = 0 și y = 0 sunt perpendiculare.
Celelalte componente ale n-tuplului x = (x1, …, xn) se numesc coordonate ale acestuia. Când n = 2 sau n = 3, prima coordonată se numește abscisă, iar a doua ordonată.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contact||||Prima pagină|||Contenit|||Geometry|||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply