Bilinear Filtering & Bilinear Interpolation

Uită-te la imaginea de mai jos. Poți calcula valorile din punctele A,B și C?

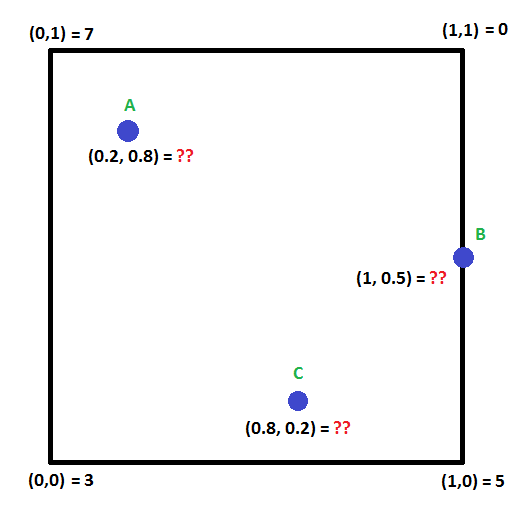
Există o tehnică pentru a face acest lucru numită interpolare biliniară care extinde ideea de interpolare liniară în două dimensiuni.

Pentru a calcula interpolarea biliniară, pur și simplu faceți interpolare liniară pe o axă și apoi pe cealaltă.

Vezi aceste exemple:

Punctul A
Punctul A are coordonatele (0,2,0,8). Să începem cu axa X.

În primul rând, vom face interpolarea prin partea de sus a pătratului de pe axa X. Asta înseamnă că trebuie să parcurgem 0,2 (20%) din drumul de la 7 la 0. Acel 0,2 este coordonata noastră pe axa X. Pentru a calcula acest lucru, procedăm astfel:
7 + (0-7) * 0,2 = 5,6

În continuare, vom face interpolarea prin partea de jos a pătratului pe axa X. Deci, similar cu cele de mai sus, vom merge 0,2 (20%) din drum de la 3 la 5. Pentru a calcula acest lucru, facem așa:
3 + (5-3) * 0,2 = 3,4

Acum că am interpolat pe axa X, trebuie să interpolăm pe axa Y. Acum vom parcurge 0,8 (80%) din drum de la valoarea noastră de jos (valoarea Y = 0), până la valoarea noastră de sus (valoarea Y = 1). Valoarea de jos este interpolarea de jos pe care am făcut-o (3,4) și valoarea de sus este interpolarea de sus pe care am făcut-o (5,6).

Deci, trebuie să mergem 0,8 (80%) din drum de la 3,4 la 5,6. Pentru a calcula acest lucru, procedăm astfel:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Înseamnă că valoarea din punctul A este 5,16. Imaginea de mai jos ar trebui să ajute la explicarea vizuală a procesului prin care am trecut.

Punctul B

Punctul B are coordonatele (1.0,0.5).

Să începem din nou cu interpolarea pe axa X (deși ați putea începe cu ușurință cu Y mai întâi, dacă ați dori! Ați ajunge la același rezultat).

Făcând interpolarea pe axa X în partea de sus, trebuie să parcurgem 1,0 (100%) din drumul de la 7 la 0. Sunt sigur că puteți ghici care este răspunsul, dar iată-l calculat:
7 + (0-7) * 1,0 = 0

În mod similar, să facem interpolarea pe axa X în partea de jos. Trebuie să parcurgem 1,0 (100%) din drumul de la 3 la 5.
3 + (5-3) * 1,0 = 5

În continuare, urmează interpolarea axei Y. Trebuie să parcurgem 0,5 (50%) din drumul de la 5 la 0.
5 + (0-5) * 0,5 = 2,5

Iată, valoarea din punctul B este 2,5. Asta ar trebui să aibă sens și dacă ne uităm la diagramă. Este practic o interpolare liniară 1d între 5 și 0 și se află la jumătatea distanței dintre ele, așa că, intuitiv, răspunsul 2,5 ar trebui să aibă sens.

Punctul C

Punctul C are o coordonată de (0,8,0,2).

Încă o dată, să facem interpolarea pe axa X în partea de sus a cutiei. Trebuie să parcurgem 0,8 (80%) din drum de la 7 la 0.
7 + (0-7) * 0,8 = 1,4

Apoi, trebuie să facem interpolarea axei X peste partea de jos a cutiei. Trebuie să parcurgem 0,8 (80%) din drum de la 3 la 5.
3 + (5-3) * 0,8 = 4,6

În cele din urmă, interpolarea axei y. Trebuie să mergem cu 0,2 (20%) de la 4,6 la 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Valoarea punctului C este 3.96

Filtrare biliniară

În timp ce interpolarea biliniară este utilă dacă aveți o grilă de date în interiorul căreia doriți să interpolați valori (cum ar fi un câmp de înălțime care reprezintă terenul?!), unde aceasta strălucește cu adevărat în dezvoltarea de jocuri este în filtrarea biliniară a texturilor.

În principiu, atunci când aveți o coordonată de textură care nu se aliniază perfect cu centrul unui pixel din textură (pentru că există un rest), se folosește partea fracționară a coordonatei din cadrul acelui pixel pentru a face interpolare biliniară între cei 4 pixeli implicați pentru a obține culoarea finală a pixelului. Interpolarea biliniară se face pe fiecare dintre canale: Roșu, Verde, Albastru și Alfa.

Rezultatul final este destul de bun! Priviți imaginea de mai jos pentru a-l vedea în acțiune pe o textură pe care am făcut un zoom prea mare. Partea stângă folosește filtrarea biliniară, în timp ce partea dreaptă nu o face, și vă arată doar cel mai apropiat pixel.

Consecvent, filtrarea biliniară a texturii trebuie să facă 4 citiri de pixeli pentru a putea interpola între ei, în loc de o singură citire de pixeli, ca atunci când se face eșantionarea prin pixelul cel mai apropiat. Mai multe citiri de pixeli = mai multă suprasolicitare și nu este la fel de ieftin (din punct de vedere computațional) de utilizat.

Links

Pentru unii dintre cei care citesc aceste informații, acestea sunt destul de elementare și s-ar putea să vă întrebați de ce m-am deranjat să scriu despre ele. Uitați-vă la următoarea postare pentru ceva oarecum bizar în ceea ce privește filtrarea biliniară. Acest lucru a fost necesar ca o piatră de hotar pentru următorul lucru pe care vreau să vi-l arăt 😛

Wikipedia: Interpolare liniară

Wikipedia: Interpolare biliniară

Wikipedia: Bilinear Filtering

The Dark Side of Bilinear Filtering

Consultați aceste link-uri pentru informații mai profunde despre unele neajunsuri (și unele soluții de rezolvare) ale eșantionării bilineare bazate pe hardware:
iq: interpolare hardware
iq: interpolare îmbunătățită a texturilor

.