9.5 – Identificarea punctelor de date influente

În această secțiune, învățăm următoarele două măsuri pentru identificarea punctelor de date influente:

• Diferența de potrivire (DFFITS)
• Distanțele lui Cook

Ideea de bază din spatele fiecăreia dintre aceste măsuri este aceeași, și anume ștergerea observațiilor una câte una, de fiecare dată refitând modelul de regresie pe cele n-1 observații rămase. Apoi, comparăm rezultatele folosind toate cele n observații cu rezultatele cu a i-a observație eliminată pentru a vedea câtă influență are observația asupra analizei. Analizând astfel, putem evalua impactul potențial pe care fiecare punct de date îl are asupra analizei de regresie.

Diferența de potrivire (DFFITS)

Diferența de potrivire pentru observația i, notată DFFITSi, se definește astfel:

\

După cum puteți vedea, numărătorul măsoară diferența dintre răspunsurile prezise obținute atunci când punctul de date ith este inclus și exclus din analiză. Numitorul este deviația standard estimată a diferenței dintre răspunsurile prezise. Prin urmare, diferența de potrivire cuantifică numărul de deviații standard pe care valoarea ajustată se modifică atunci când al i-lea punct de date este omis.

O observație este considerată influentă dacă valoarea absolută a valorii sale DFFITS este mai mare decât:

\

unde, ca întotdeauna, n = numărul de observații și k = numărul de termeni predictori (adică numărul de parametri de regresie, cu excepția interceptului). Este important să rețineți că aceasta nu este o regulă strictă, ci mai degrabă doar o linie directoare! Nu este greu de găsit autori diferiți care utilizează o linie directoare ușor diferită. Prin urmare, eu prefer adesea o linie directoare mult mai subiectivă, cum ar fi faptul că un punct de date este considerat influent dacă valoarea absolută a valorii sale DFFITS iese în evidență ca un deget mare dintre celelalte valori DFFITS. Desigur, aceasta este o judecată calitativă, poate așa cum ar trebui să fie, deoarece valorile aberante, prin însăși natura lor, sunt cantități subiective.

Exemplu #2 (din nou). Să verificăm măsura diferenței de potrivire pentru acest set de date (influence2.txt):

Regresând y în funcție de x și solicitând diferența în ajustări, obținem următoarea ieșire software:

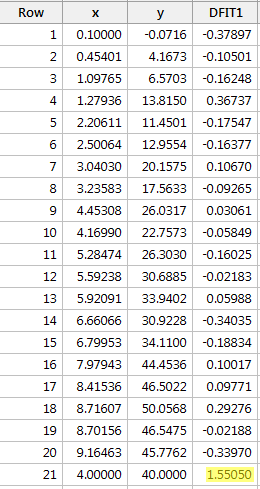
Utilizând ghidul obiectiv definit mai sus, considerăm că un punct de date este influent dacă valoarea absolută a valorii sale DFFITS este mai mare decât:

\

Doar un singur punct de date – cel roșu – are o valoare DFFITS a cărei valoare absolută (1.55050) este mai mare de 0,82. Prin urmare, pe baza acestei orientări, vom considera că punctul de date roșu este influent.

Exemplul #3 (din nou). Să verificăm măsura diferenței de potrivire pentru acest set de date (influence3.txt):

Regresând y pe x și solicitând diferența în ajustări, obținem următoarea ieșire software:

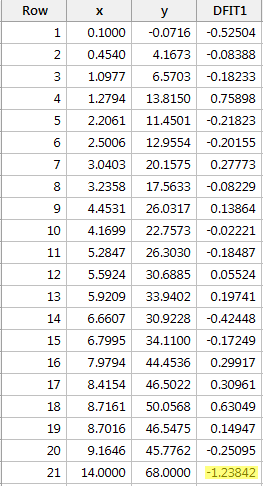
Utilizând ghidul obiectiv definit mai sus, considerăm că un punct de date este influent dacă valoarea absolută a valorii sale DFFITS este mai mare decât:

\

Doar un singur punct de date – cel roșu – are o valoare DFFITS a cărei valoare absolută (1.23841) este mai mare decât 0,82. Prin urmare, pe baza acestei orientări, am considera punctul de date roșu ca fiind influent.

Când am studiat acest set de date la începutul acestei lecții, am decis că punctul de date roșu nu a afectat prea mult analiza de regresie. Cu toate acestea, aici, diferența în măsura ajustărilor sugerează că este într-adevăr influent. Ce se întâmplă aici? Totul se reduce la recunoașterea faptului că toate măsurile din această lecție sunt doar instrumente care semnalează puncte de date potențial influente pentru analistul de date. În cele din urmă, analistul ar trebui să analizeze setul de date de două ori – o dată cu și o dată fără punctele de date semnalate. Dacă punctele de date modifică în mod semnificativ rezultatul analizei de regresie, atunci cercetătorul ar trebui să raporteze rezultatele ambelor analize.

În mod întâmplător, în acest exemplu de aici, dacă folosim orientarea mai subiectivă de a vedea dacă valoarea absolută a valorii DFFITS iese în evidență ca un deget mare, este probabil să nu considerăm punctul de date roșu ca fiind influent. La urma urmei, următoarea cea mai mare valoare DFFITS (în valoare absolută) este 0,75898. Această valoare DFFITS nu este atât de diferită de valoarea DFFITS a punctului nostru de date „influent”.

Exemplul nr. 4 (din nou). Să verificăm măsura diferenței de potrivire pentru acest set de date (influence4.txt):

Regresând y pe x și solicitând diferența în ajustări, obținem următoarea ieșire software:

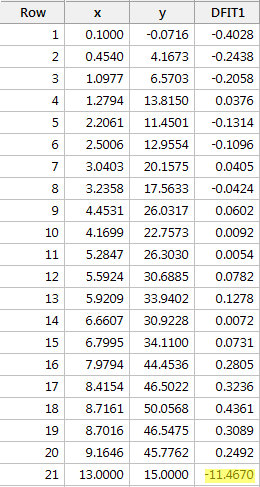
Utilizând ghidul obiectiv definit mai sus, considerăm din nou că un punct de date este influent dacă valoarea absolută a valorii sale DFFITS este mai mare decât:

\

Ce părere aveți? Iese în evidență vreuna dintre valorile DFFITS? Errr – valoarea DFFITS a punctului de date roșu (-11,4670 ) este cu siguranță de o magnitudine diferită față de toate celelalte. În acest caz, nu ar trebui să existe prea multe îndoieli că punctul de date roșu este influent!

Distanța lui Cook

Să sărim direct aici, măsura distanței lui Cook, notată Di, este definită astfel:

.\\]

Apare puțin dezordonat, dar principalul lucru care trebuie recunoscut este că Di al lui Cook depinde atât de rezidual, ei (în primul termen), cât și de efectul de pârghie, hii (în al doilea termen). Adică, atât valoarea x, cât și valoarea y a punctului de date joacă un rol în calculul distanței lui Cook.

În concluzie:

• Di rezumă direct cât de mult se schimbă toate valorile ajustate atunci când este eliminată a i-a observație.
• Un punct de date care are un Di mare indică faptul că punctul de date influențează puternic valorile ajustate.

Să investigăm ce înseamnă exact această primă afirmație în contextul unora dintre exemplele noastre.

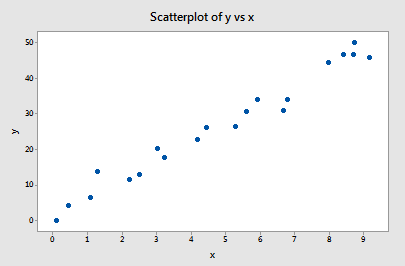
Exemplul #1 (din nou). Poate vă amintiți că reprezentarea grafică a acestor date (influence1.txt) sugerează că nu există puncte de date aberante și nici puncte de date influente pentru acest exemplu:

Dacă facem o regresie a lui y în funcție de x folosind toate cele n = 20 de puncte de date, determinăm că coeficientul de interceptare estimat b0 = 1,732 și coeficientul de pantă estimat b1 = 5,117. Dacă eliminăm primul punct de date din setul de date și efectuăm o regresie a lui y în funcție de x utilizând restul de n = 19 puncte de date, determinăm că coeficientul de interceptare estimat b0 = 1,732 și coeficientul de pantă estimat b1 = 5,1169. După cum sperăm și ne așteptăm, estimările nu se schimbă foarte mult atunci când eliminăm un punct de date. Continuând acest proces de eliminare a fiecărui punct de date, pe rând, și trasând grafic pantele estimate rezultate (b1) față de interceptările estimate (b0), obținem:

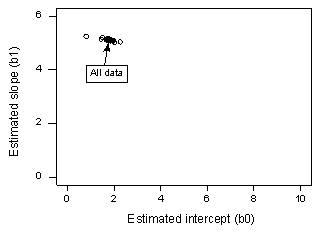
Punctul negru solid reprezintă coeficienții estimați pe baza tuturor celor n = 20 de puncte de date. Cercurile deschise reprezintă fiecare dintre coeficienții estimați obținuți atunci când se șterge fiecare punct de date, unul câte unul. După cum se poate observa, coeficienții estimați sunt toți grupați împreună, indiferent de punctul de date care este eliminat, dacă este cazul. Acest lucru sugerează că niciun punct de date nu influențează în mod nejustificat funcția de regresie estimată sau, la rândul său, valorile ajustate. În acest caz, ne-am aștepta ca toate măsurile de distanță ale lui Cook, Di, să fie mici.

Exemplul #4 (din nou). Poate vă amintiți că reprezentarea grafică a acestor date (influence4.txt) sugerează că un punct de date este influent și aberant pentru acest exemplu:

Dacă facem o regresie de la y la x folosind toate cele n = 21 puncte de date, determinăm că coeficientul de interceptare estimat b0 = 8,51 și coeficientul de pantă estimat b1 = 3,32. Dacă eliminăm punctul de date roșu din setul de date și regresăm y în funcție de x utilizând restul de n = 20 de puncte de date, determinăm că coeficientul de interceptare estimat b0 = 1,732 și coeficientul de pantă estimat b1 = 5,1169. Wow – estimările se schimbă substanțial la eliminarea unui punct de date. Continuând acest proces de eliminare a fiecărui punct de date, pe rând, și trasând pantele estimate (b1) rezultate în raport cu interceptările estimate (b0), obținem:

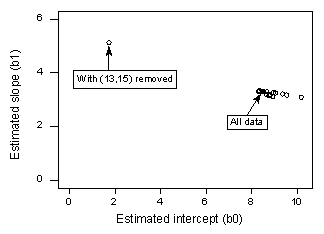
Din nou, punctul negru solid reprezintă coeficienții estimați pe baza tuturor celor n = 21 puncte de date. Cercurile deschise reprezintă fiecare dintre coeficienții estimați obținuți atunci când se elimină fiecare punct de date unul câte unul. După cum puteți vedea, cu excepția punctului de date roșu (x = 13, y = 15), coeficienții estimați sunt toți grupați împreună, indiferent de punctul de date care este eliminat, dacă este cazul. Acest lucru sugerează că punctul de date roșu este singurul punct de date care influențează în mod nejustificat funcția de regresie estimată și, la rândul său, valorile ajustate. În acest caz, ne-am aștepta ca măsura distanței lui Cook, Di, pentru punctul de date roșu să fie mare, iar măsurile distanței lui Cook, Di, pentru celelalte puncte de date să fie mici.

Utilizarea măsurilor de distanță ale lui Cook. Frumusețea exemplelor de mai sus constă în capacitatea de a vedea ce se întâmplă cu ajutorul unor diagrame simple. Din păcate, nu ne putem baza pe diagrame simple în cazul regresiei multiple. În schimb, trebuie să ne bazăm pe liniile directoare pentru a decide când o măsură a distanței lui Cook este suficient de mare pentru a justifica tratarea unui punct de date ca fiind influent.

Iată liniile directoare utilizate în mod obișnuit:

• Dacă Di este mai mare de 0,5, atunci al i-lea punct de date merită o investigație suplimentară, deoarece poate fi influent.
• Dacă Di este mai mare de 1, atunci este foarte probabil ca al i-lea punct de date să fie influent.
• Sau, dacă Di iese în evidență ca un deget mare față de celelalte valori Di, este aproape sigur că este influent.

Exemplul nr. 2 (din nou). Să verificăm măsura distanței lui Cook pentru acest set de date (influence2.txt):

Regresând y pe x și solicitând măsurile de distanță ale lui Cook, obținem următoarea ieșire software:

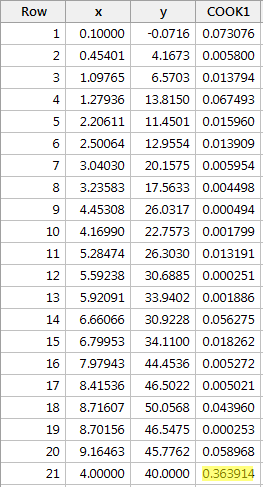
Măsura de distanță a lui Cook pentru punctul de date roșu (0,363914) iese puțin în evidență în comparație cu celelalte măsuri de distanță ale lui Cook. Cu toate acestea, măsura distanței lui Cook pentru punctul de date roșu este mai mică de 0,5. Prin urmare, pe baza măsurii distanței lui Cook, nu am clasifica punctul de date roșu ca fiind influent.

Exemplul #3 (din nou). Să verificăm măsura distanței lui Cook pentru acest set de date (influence3.txt):

Regresând y pe x și solicitând măsurile de distanță ale lui Cook, obținem următoarea ieșire software:

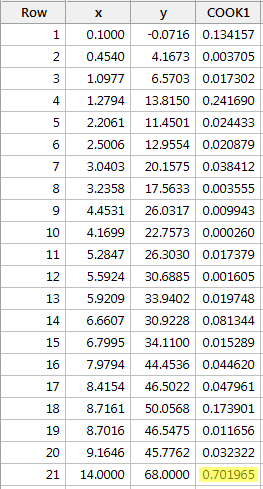
Măsura de distanță a lui Cook pentru punctul de date roșu (0,701965) iese puțin în evidență în comparație cu celelalte măsuri de distanță ale lui Cook. Totuși, măsura distanței lui Cook pentru punctul de date roșu este mai mare decât 0,5, dar mai mică decât 1. Prin urmare, pe baza măsurii distanței lui Cook, poate că am investiga mai departe, dar nu am clasifica neapărat punctul de date roșu ca fiind influent.

Exemplul #4 (din nou). Să verificăm măsura distanței lui Cook pentru acest set de date (influence4.txt):

Regresând y în funcție de x și solicitând măsurile distanței lui Cook, obținem următoarea ieșire software:

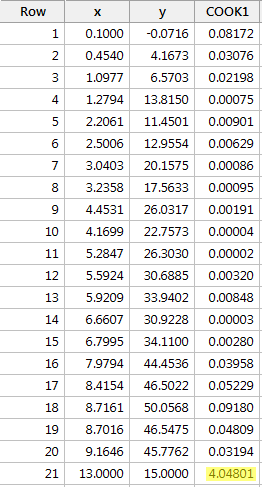
În acest caz, măsura distanței lui Cook pentru punctul de date roșu (4.04801) se evidențiază substanțial în comparație cu celelalte măsuri de distanță ale lui Cook. Mai mult decât atât, măsura distanței lui Cook pentru punctul de date roșu este mai mare decât 1. Prin urmare, pe baza măsurii distanței lui Cook – și nu este surprinzător – am clasifica punctul de date roșu ca fiind influent.

O metodă alternativă de interpretare a distanței lui Cook care este utilizată uneori este de a raporta măsura la distribuția F(k+1, n-k-1) și de a găsi valoarea percentila corespunzătoare. Dacă această percentilă este mai mică de aproximativ 10 sau 20 de procente, atunci cazul are o influență aparentă redusă asupra valorilor ajustate. Pe de altă parte, dacă se apropie de 50 % sau chiar mai mult, atunci cazul are o influență majoră. (Orice lucru „între” este mai ambiguu.)