Uma introdução suave ao problema do casco convexo

Cascos convexos tendem a ser úteis em muitos campos diferentes, às vezes de forma bastante inesperada. Neste artigo, vou explicar a idéia básica dos cascos convexos 2d e como usar o graham scan para encontrá-los. Então se você já sabe sobre o graham scan, então este artigo não é para você, mas se não, isto deve familiarizá-lo com alguns dos conceitos relevantes.

O casco convexo de um conjunto de pontos é definido como o menor polígono convexo, que encerra todos os pontos do conjunto. Convexo significa que o polígono não tem nenhum canto dobrado para dentro.

As bordas vermelhas no polígono direito delimitam o canto onde a forma é côncava, o oposto do convexo.

Uma forma útil de pensar sobre o casco convexo é a analogia do elástico de borracha. Suponhamos que os pontos do conjunto fossem pregos, saindo de uma superfície plana. Imagine agora, o que aconteceria se você pegasse um elástico e o esticasse ao redor dos pregos. Tentando contrair-se de volta ao seu comprimento original, o elástico fecharia os pregos, tocando nos que mais se destacassem do centro.

>

>

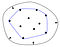
Para representar o casco convexo resultante em código, geralmente armazenamos a lista de pontos que sustentam este elástico, ou seja, a lista de pontos no casco convexo.

Nota que ainda precisamos definir o que deve acontecer se três pontos estiverem na mesma linha. Se você imaginar que o elástico tem um ponto onde ele toca um dos pregos mas não se dobra ali, isso significa que o prego ali está em uma linha reta entre dois outros pregos. Dependendo do problema, podemos considerar esse prego ao longo da linha reta como parte da saída, já que ele toca o elástico. Por outro lado, podemos também dizer que este prego não deve fazer parte da saída, porque a forma do elástico não muda quando o retiramos. Esta decisão depende do problema em que você está trabalhando atualmente, e o melhor de tudo se você tem uma entrada onde não há três pontos colineares (este é muitas vezes o caso em tarefas fáceis de programação de competições) então você pode até mesmo ignorar completamente este problema.

Localizar o casco convexo

Localizar um conjunto de pontos, a intuição humana nos permite rapidamente descobrir quais pontos são susceptíveis de tocar o casco convexo, e quais serão mais próximos do centro e, portanto, longe do casco convexo. Mas traduzir esta intuição em código requer um pouco de trabalho.

Para encontrar o casco convexo de um conjunto de pontos, podemos usar um algoritmo chamado Graham Scan, que é considerado um dos primeiros algoritmos de geometria computacional. Usando este algoritmo, podemos encontrar o subconjunto de pontos que se encontram no casco convexo, juntamente com a ordem em que estes pontos são encontrados ao contornar o casco convexo.

O algoritmo começa com a procura de um ponto, que sabemos que se encontra no casco convexo com certeza. O ponto com a menor coordenada y, por exemplo, pode ser considerado uma escolha segura. Se existirem vários pontos na mesma coordenada y, tomamos aquele que tem a maior coordenada x (isto também funciona com outros pontos de canto, por exemplo, primeiro o ponto mais baixo x e depois o mais baixo y).

Próximo, ordenamos os outros pontos pelo ângulo em que se encontram, tal como visto desde o ponto de partida. Se dois pontos estiverem no mesmo ângulo, o ponto mais próximo do ponto de partida deve ocorrer mais cedo na ordenação.

Agora, a ideia do algoritmo é andar à volta desta ordenação, determinando para cada ponto, se este se encontra ou não no casco convexo. Isto significa, que para cada triplo de pontos que encontramos, nós decidimos se eles formam um canto convexo ou côncavo. Se o canto é côncavo, então sabemos que o ponto central deste trigêmeo não pode estar sobre o casco convexo.

(Note que os termos canto côncavo e convexo devem ser usados em relação a todo o polígono, apenas um canto por si só não pode ser convexo ou côncavo, já que não haveria nenhuma direção de referência.)

Armazenamos os pontos que se encontram no casco convexo numa pilha, dessa forma podemos adicionar pontos se os alcançarmos no caminho ao redor dos pontos ordenados, e removê-los se descobrirmos que eles formam um canto côncavo.

(A rigor, temos de aceder aos dois pontos superiores da pilha, por isso usamos um std::vector em vez disso, mas pensamos nele como uma espécie de pilha, porque estamos sempre preocupados apenas com os elementos superiores.)

Contornando o conjunto de pontos ordenados, adicionamos o ponto à pilha, e se mais tarde descobrirmos que o ponto não pertence ao casco convexo, removemo-lo.

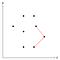
Podemos medir se o canto actual se dobra para dentro ou para fora calculando o produto cruzado e verificando se este é positivo ou negativo. A figura acima mostra um triplo de pontos onde o canto que eles formam é convexo, portanto o do meio desses três pontos permanece na pilha por enquanto.

Vai para o próximo ponto, continuamos fazendo a mesma coisa: verificar se o canto é convexo e, se não for, remover o ponto. Depois continuamos a adicionar o próximo ponto e repetimos.

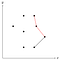
Este canto marcado a vermelho é côncavo, portanto removemos o ponto médio da pilha, pois não pode fazer parte do casco convexo.

Como sabemos que isto nos dará a resposta correcta?

Escrever uma prova rigorosa está fora do âmbito deste artigo, mas posso anotar as ideias básicas. Contudo, encorajo-o a continuar e tentar preencher as lacunas!

Desde que calculámos o produto cruzado em cada canto, sabemos com certeza que estamos a receber um polígono convexo. Agora só temos que provar, que este polígono convexo realmente engloba todos os pontos.

(Na verdade, você também precisaria mostrar que este é o menor polígono convexo possível satisfazendo estas condições, mas isso se segue facilmente dos pontos de canto do nosso polígono convexo sendo um subconjunto do conjunto original de pontos.)

Suponha, existe um ponto P fora do polígono que acabamos de encontrar.

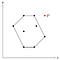
Desde que cada ponto tenha sido adicionado à pilha uma vez, sabemos que o P foi removido da pilha em algum ponto. Isto significa, que P, juntamente com seus pontos vizinhos, vamos chamá-los de O e Q, formou um canto côncavo.

Desde que O e Q estão dentro do polígono (ou em sua borda), P teria que estar dentro da borda também, porque o polígono é convexo e o canto que O e Q formam com P é côncavo em relação ao polígono.

Então encontramos uma contradição, o que significa que tal ponto P não pode existir.

Implementação

A implementação aqui fornecida tem uma função convex_hull, que leva um std::vector que contém os pontos como std::pairs de ints e retorna outro std::vector que contém os pontos que se encontram no casco convexo.

Análise de tempo de execução e memória

É sempre útil pensar nos algoritmos de complexidade em termos da notação Big-O, que não vou explicar aqui, porque aqui o Michael Olorunnisola já fez um trabalho muito melhor do que eu provavelmente faria:

A classificação dos pontos leva inicialmente tempo O(n log n), mas depois disso, cada passo pode ser calculado em tempo constante. Cada ponto é adicionado e removido da pilha no máximo uma vez, isto significa que o pior caso de tempo de execução está em O(n log n).

O uso da memória, que está em O(n) no momento, poderia ser otimizado removendo a necessidade da pilha e executando as operações diretamente no array de entrada. Nós poderíamos mover os pontos que se encontram no casco convexo para o início do array de entrada e organizá-los na ordem correta, e os outros pontos seriam movidos para o resto do array. A função poderia então retornar apenas uma única variável inteira que denota a quantidade de pontos no array que se encontram no casco convexo. Isto, é claro, tem o lado negativo, que a função fica muito mais complicada, portanto eu desaconselharia, a menos que você esteja codificando para sistemas embutidos ou tenha preocupações de memória similarmente restritivas. Para a maioria das situações, a probabilidade de erro/reserva de memória não vale a pena.

Outros Algoritmos

Uma alternativa ao Graham Scan é o algoritmo de Chan, que é baseado efetivamente na mesma idéia, mas é mais fácil de implementar. Faz sentido primeiro entender como o Graham Scan funciona.

Se você está realmente se sentindo extravagante e quer resolver o problema em três dimensões, dê uma olhada no algoritmo introduzido pela Preparata e Hong em seu artigo de 1977 “Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.