Uma breve introdução à privacidade diferencial
Aaruran Elamurugaiyan
Privacidade pode ser quantificada. Melhor ainda, podemos classificar as estratégias de preservação da privacidade e dizer qual delas é mais eficaz. Melhor ainda, podemos desenhar estratégias que sejam robustas mesmo contra hackers que tenham informação auxiliar. E como se isso não fosse suficientemente bom, podemos fazer todas essas coisas simultaneamente. Estas soluções, e mais, residem numa teoria probabilística chamada privacidade diferencial.
Aqui está o contexto. Estamos curando (ou gerenciando) uma base de dados sensível e gostaríamos de liberar algumas estatísticas desses dados para o público. No entanto, temos de garantir que é impossível para um adversário reverter os dados sensíveis a partir do que lançamos . Um adversário neste caso é uma parte com a intenção de revelar, ou de aprender, pelo menos alguns dos nossos dados sensíveis. A privacidade diferencial pode resolver problemas que surgem quando esses três ingredientes – dados sensíveis, curadores que precisam divulgar estatísticas e adversários que querem recuperar os dados sensíveis – estão presentes (ver Figura 1). Esta engenharia reversa é um tipo de violação de privacidade.

Mas quão difícil é violar a privacidade? A anonimização dos dados não seria suficientemente boa? Se você tiver informações auxiliares de outras fontes de dados, a anonimização não é suficiente. Por exemplo, em 2007, o Netflix lançou um conjunto de dados de suas classificações de usuários como parte de uma competição para ver se alguém pode superar seu algoritmo de filtragem colaborativa. O conjunto de dados não continha informações de identificação pessoal, mas os pesquisadores ainda conseguiram violar a privacidade; eles recuperaram 99% de todas as informações pessoais que foram removidas do conjunto de dados. Neste caso, os pesquisadores violaram a privacidade usando informações auxiliares do IMDB.
Como alguém pode se defender contra um adversário que tem ajuda desconhecida, e possivelmente ilimitada, do mundo exterior? A privacidade diferencial oferece uma solução. Algoritmos diferencialmente privados são resistentes a ataques adaptativos que utilizam informação auxiliar . Estes algoritmos dependem da incorporação de ruído aleatório na mistura para que tudo o que um adversário recebe se torne barulhento e impreciso, e assim é muito mais difícil violar a privacidade (se for viável).
Contagem de ruído
Vejamos um exemplo simples de injeção de ruído. Suponha que gerenciamos uma base de dados de classificação de crédito (resumida pela Tabela 1).
Para este exemplo, vamos supor que o adversário quer saber o número de pessoas que têm uma má classificação de crédito (que é 3). Os dados são sensíveis, por isso não podemos revelar a verdade do terreno. Em vez disso, vamos usar um algoritmo que retorna a verdade do terreno, N = 3, mais algum ruído aleatório. Esta ideia básica (adicionar ruído aleatório à verdade sobre o solo) é a chave para a privacidade diferencial. Digamos que escolhemos um número aleatório L a partir de uma distribuição Laplace centrada no zero com desvio padrão de 2. Nós retornamos N+L. Vamos explicar a escolha do desvio padrão em alguns parágrafos. (Se você ainda não ouviu falar da distribuição Laplace, veja a Figura 2). Vamos chamar este algoritmo de “contagem ruidosa”.
Se vamos relatar uma resposta disparatada e barulhenta, qual é o objectivo deste algoritmo? A resposta é que ele nos permite encontrar um equilíbrio entre utilidade e privacidade. Queremos que o público em geral ganhe alguma utilidade da nossa base de dados, sem expor quaisquer dados sensíveis a um possível adversário.
O que o adversário realmente receberia? As respostas são relatadas na Tabela 2.

A primeira resposta que o adversário recebe é próxima, mas não igual, à verdade do terreno. Nesse sentido, o adversário é enganado, a utilidade é fornecida e a privacidade é protegida. Mas após múltiplas tentativas, eles serão capazes de estimar a verdade do terreno. Essa “estimativa a partir de consultas repetidas” é uma das limitações fundamentais da privacidade diferencial . Se o adversário puder fazer consultas suficientes a uma base de dados diferencialmente privada, ele ainda poderá estimar os dados sensíveis. Em outras palavras, com cada vez mais consultas, a privacidade é violada. A Tabela 2 demonstra empiricamente essa violação de privacidade. Entretanto, como você pode ver, o intervalo de confiança de 90% dessas 5 consultas é bastante amplo; a estimativa ainda não é muito precisa.
Quão precisa pode ser essa estimativa? Dê uma olhada na Figura 3 onde fizemos uma simulação várias vezes e plotamos os resultados .

Cada linha vertical ilustra a largura de um intervalo de confiança de 95%, e os pontos indicam a média dos dados amostrados do adversário. Note que estes gráficos têm um eixo horizontal logarítmico, e que o ruído é extraído de variáveis aleatórias Laplace independentes e distribuídas de forma idêntica. Em geral, a média é mais ruidosa com menos consultas (uma vez que os tamanhos das amostras são pequenos). Como esperado, os intervalos de confiança tornam-se mais estreitos à medida que o adversário faz mais consultas (uma vez que o tamanho da amostra aumenta, e as médias de ruído chegam a zero). Só de inspecionar o gráfico, podemos ver que são necessárias cerca de 50 consultas para fazer uma estimativa decente.
Vamos refletir sobre esse exemplo. Primeiro e acima de tudo, ao adicionar ruído aleatório, tornamos mais difícil para um adversário violar a privacidade. Em segundo lugar, a estratégia de ocultação que empregamos foi simples de implementar e entender. Infelizmente, com mais e mais consultas, o adversário foi capaz de aproximar a contagem verdadeira.
Se aumentarmos a variação do ruído adicionado, podemos defender melhor os nossos dados, mas não podemos simplesmente adicionar qualquer ruído Laplace a uma função que queremos ocultar. A razão é que a quantidade de ruído que devemos adicionar depende da sensibilidade da função, e cada função tem a sua própria sensibilidade. Em particular, a função de contagem tem uma sensibilidade de 1. Vamos dar uma olhada no que significa sensibilidade neste contexto.
Sensibilidade e o mecanismo de Laplace
Para uma função:
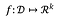
a sensibilidade de f é:
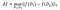
em conjuntos de dados D₁, D₂ diferindo em, no máximo, um elemento .
A definição acima é bastante matemática, mas não é tão má quanto parece. Grosso modo, a sensibilidade de uma função é a maior diferença possível que uma linha pode ter sobre o resultado dessa função, para qualquer conjunto de dados. Por exemplo, em nosso conjunto de dados de brinquedos, a contagem do número de linhas tem uma sensibilidade de 1, porque adicionar ou remover uma única linha de qualquer conjunto de dados irá alterar a contagem em no máximo 1,
Como outro exemplo, suponha que pensemos em “contagem arredondada para um múltiplo de 5”. Esta função tem uma sensibilidade de 5, e podemos mostrar isto com bastante facilidade. Se tivermos dois conjuntos de dados de tamanho 10 e 11, eles diferem em uma linha, mas as “contagens arredondadas para um múltiplo de 5” são 10 e 15, respectivamente. Na verdade, cinco é a maior diferença possível que esta função de exemplo pode produzir. Portanto, sua sensibilidade é 5,
Calcular a sensibilidade para uma função arbitrária é difícil. Um esforço considerável de pesquisa é gasto na estimativa das sensibilidades, melhorando as estimativas da sensibilidade e contornando o cálculo da sensibilidade .
Como a sensibilidade se relaciona com a contagem de ruídos? Nossa estratégia de contagem ruidosa utilizou um algoritmo chamado mecanismo de Laplace, que por sua vez se baseia na sensibilidade da função que obscurece. No algoritmo 1, temos uma implementação ingênua de pseudo-código do mecanismo de Laplace .
Algoritmo 1
Input: Função F, Entrada X, Nível de privacidade ϵ
Saída: Uma resposta ruidosa
Cálculo F (X)
Cálculo da sensibilidade de F : S
Ruído L de uma distribuição Laplace com variância:
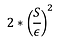
Retorno F(X) + L
Quanto maior for a sensibilidade S, mais ruidosa será a resposta. A contagem só tem uma sensibilidade de 1, portanto não precisamos adicionar muito ruído para preservar a privacidade.
Note que o mecanismo Laplace no Algoritmo 1 consome um parâmetro epsilon. Vamos nos referir a esta quantidade como a perda de privacidade do mecanismo e é parte da definição mais central no campo da privacidade diferencial: epsilon-diferencial privacidade. Para ilustrar, se recordarmos o nosso exemplo anterior e usarmos alguma álgebra, podemos ver que o nosso mecanismo de contagem ruidosa tem privacidade diferencial epsilon, com um epsilon de 0,707. Ao sintonizar o epsilon, controlamos o ruído da nossa contagem ruidosa. A escolha de um epsilon menor produz resultados mais ruidosos e melhores garantias de privacidade. Como referência, a Apple usa um epsilon de 2 em seu teclado com correção automática diferencial de privacidade .
A quantidade de epsilon é como a privacidade diferencial pode fornecer comparações rigorosas entre diferentes estratégias. A definição formal de privacidade diferencial do epsilon é um pouco mais matematicamente envolvida, por isso omiti-a intencionalmente neste post do blog. Você pode ler mais sobre isso na pesquisa do Dwork sobre privacidade diferencial .
Como você se lembra, o exemplo de contagem ruidosa tinha um epsilon de 0,707, que é bem pequeno. Mas nós ainda violamos a privacidade após 50 consultas. Porquê? Porque com o aumento das consultas, o orçamento de privacidade cresce, e portanto a garantia de privacidade é pior.
O orçamento de privacidade
Em geral, as perdas de privacidade acumulam-se. Quando duas respostas são devolvidas a um adversário, a perda total de privacidade é duas vezes maior, e a garantia de privacidade é metade mais forte. Esta propriedade acumulada é uma consequência do teorema da composição. Em essência, a cada nova consulta, informações adicionais sobre os dados sensíveis são liberadas. Assim, o teorema da composição tem uma visão pessimista e assume o pior cenário possível: a mesma quantidade de vazamento acontece a cada nova resposta. Para uma forte garantia de privacidade, queremos que a perda de privacidade seja pequena. Então em nosso exemplo onde temos perda de privacidade de trinta e cinco (após 50 consultas ao nosso mecanismo de contagem de ruídos de Laplace), a garantia de privacidade correspondente é frágil.
Como a privacidade diferencial funciona se a perda de privacidade cresce tão rapidamente? Para garantir uma garantia de privacidade significativa, os curadores de dados podem impor uma perda máxima de privacidade. Se o número de consultas exceder o limite, então a garantia de privacidade torna-se demasiado fraca e o curador deixa de responder às consultas. A perda máxima de privacidade é chamada de orçamento de privacidade . Podemos pensar em cada consulta como uma ‘despesa’ de privacidade que incorre numa perda incremental de privacidade. A estratégia de usar orçamentos, despesas e perdas é adequadamente conhecida como contabilidade de privacidade .
A contabilidade de privacidade é uma estratégia eficaz para computar a perda de privacidade após múltiplas consultas, mas ainda pode incorporar o teorema da composição. Como observado anteriormente, o teorema da composição assume o pior cenário possível. Em outras palavras, existem melhores alternativas.
Deep Learning
Deep Learning é um subcampo de aprendizagem de máquina, que diz respeito ao treinamento de redes neurais profundas (DNNs) para estimar funções desconhecidas . (A um alto nível, um DNN é uma sequência de transformações afins e não lineares que mapeia algum espaço n-dimensional para um espaço m-dimensional). As suas aplicações são generalizadas e não precisam de ser repetidas aqui. Vamos explorar como treinar privadamente uma rede neural profunda.
As redes neurais profundas são tipicamente treinadas usando uma variante de descida de gradiente estocástico (SGD). Abadi et al. inventaram uma versão de preservação de privacidade deste popular algoritmo, comumente chamado de “SGD privado” (ou PSGD). A Figura 4 ilustra o poder de sua nova técnica . Abadi et al. inventaram uma nova abordagem: o contador de momentos. A idéia básica por trás do contador de momentos é acumular os gastos com privacidade, enquadrando a perda de privacidade como uma variável aleatória e usando suas funções geradoras de momento para entender melhor a distribuição dessa variável (daí o nome) . Os detalhes técnicos completos estão fora do escopo de um post introdutório no blog, mas nós encorajamos você a ler o artigo original para saber mais.

Pensamentos finais
Revisamos a teoria da privacidade diferencial e vimos como ela pode ser usada para quantificar a privacidade. Os exemplos neste post mostram como as idéias fundamentais podem ser aplicadas e a conexão entre aplicação e teoria. É importante lembrar que as garantias de privacidade se deterioram com o uso repetido, então vale a pena pensar em como mitigar isso, seja com orçamentos de privacidade ou outras estratégias. Você pode investigar a deterioração clicando nesta frase e repetindo as nossas experiências. Há ainda muitas perguntas não respondidas aqui e uma grande quantidade de literatura para explorar – veja as referências abaixo. Nós encorajamos você a ler mais.
Cynthia Dwork. Privacidade diferencial: Um levantamento dos resultados. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Laplace distribution, julho 2018.
Aaruran Elamurugaiyan. Lotes demonstrando erro padrão de respostas diferentemente privadas sobre o número de consultas, agosto 2018.
Benjamin I. P. Rubinstein e Francesco Alda. Privacidade diferencial aleatória sem dor com amostragem de sensibilidade. Em 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork e Aaron Roth. Os fundamentos algorítmicos da privacidade diferencial . Agora Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, e Li Zhang. Aprendizagem profunda com privacidade diferencial. Anais da Conferência ACM SIGSAC 2016 sobre Segurança de Computadores e Comunicações – CCS16 , 2016.
Frank D. McSherry. Consultas integradas de privacidade: Uma plataforma expansível para análise de dados de preservação da privacidade. Em Actas da Conferência Internacional ACM SIGMOD 2009 sobre Gestão de Dados , SIGMOD ’09, páginas 19-30, Nova Iorque, NY, EUA, 2009. ACM.
Contribuintes da Wikipedia. Deep Learning, Agosto 2018.
Leave a Reply