Ressonância de Helmholtz
- Análise da ressonância de Helmholtz
- Ressonância, impedância, dependência de fase e frequência
- Complicações envolvendo o comprimento
- Ressonâncias de Helmholtz e guitarras
Análise da ressonância de Helmholtz
Agora vamos obter quantitativos: Em primeiro lugar, vamos assumir que o comprimento de onda do som produzido é muito maior que as dimensões do ressonador. Para as garrafas da animação no topo desta página, os comprimentos de onda são de 180 e 74 cm respectivamente, por isso esta aproximação é bastante boa, mas vale a pena verificar sempre que se começa a descrever algo como um oscilador de Helmholtz. A consequência desta aproximação é que podemos negligenciar as variações de pressão dentro do volume do recipiente: a oscilação de pressão terá a mesma fase em todo o interior do recipiente.
Deixe o ar no pescoço ter um comprimento efetivo L e uma área transversal S. Sua massa é então SL vezes a densidade do ar ρ. (Algumas complicações sobre o comprimento efetivo são discutidas no final desta página). Se este ‘tampão’ de ar descer uma pequena distância x para dentro da garrafa, ele comprime o ar no recipiente de modo que o ar que antes ocupava o volume V tenha agora o volume V – Sx. Consequentemente, a pressão desse ar sobe da pressão atmosférica PA para um valor mais alto PA + p.
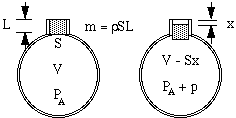
Agora você pode pensar que o aumento de pressão seria apenas proporcional à diminuição do volume. Isso seria o caso se a compressão ocorresse tão lentamente que a temperatura não mudasse. Em vibrações que dão origem ao som, no entanto, as mudanças são rápidas e assim a temperatura sobe com a compressão, dando uma mudança maior na pressão. Tecnicamente são adiabáticas, o que significa que o calor não tem tempo para se mover, e a equação resultante envolve uma constante γ, a razão de aquecimento específico, que é de cerca de 1,4 para o ar. (Isto é explicado em um apêndice.) Como resultado, a mudança de pressão p produzida por uma pequena mudança de volume ΔV é apenas
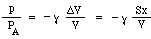
Agora a massa m é movida pela diferença de pressão entre a parte superior e inferior do pescoço, ou seja, uma força nett pS, então escrevemos a lei de Newton para a aceleração a:
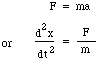
substituindo F e m dá: 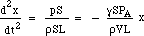
Assim a força restauradora é proporcional ao deslocamento. Esta é a condição para o Movimento Harmónico Simples, e tem uma frequência que é 1/2π vezes a raiz quadrada da constante de proporcionalidade, portanto
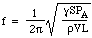
Agora a velocidade c do som no ar é determinada pela densidade, a pressão e a razão de aquecimento específico, para que possamos escrever:
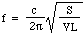
Vamos colocar alguns números: para uma garrafa de 1 litro, com S = 3 centímetros quadrados e L = 5 centímetros, a frequência é de 130 Hz, que é cerca do Dó abaixo do C médio. (Ver notas.) Então o comprimento de onda é de 2,6 metros, que é muito maior que a garrafa. Isto justifica, post hoc, a suposição feita no início da derivação.
Resonância, impedância, dependência de fase e frequência
Esta secção pode ser lida por si só, mas se quiser um fundo mais detalhado, veja Oscilações, Oscilações Forçadas e Conformidade Acústica, Inertância e Impedância.
Vamos voltar à representação mecânica e olhar para o ressonador Helmholtz do exterior, como mostra o primeiro esquema: estamos empurrando com uma força oscilatória F, com freqüência f ,a massa m (o ar no pescoço do ressonador), que é suportada na mola (o ar fechado) com a constante k da mola, cuja outra extremidade é fixa (o ar no ressonador não pode escapar). Irrealisticamente, vamos negligenciar a gravidade e o atrito (por enquanto).
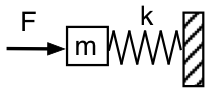
A força necessária para acelerar a massa é proporcional à aceleração e por isso proporcional a f2. A uma frequência suficientemente baixa, a força necessária para acelerar a massa é insignificante, por isso F só tem que comprimir e estender a mola. Assim, nesse limite, a força aplicada F = +kx. (A força da mola é -kx.) A impedância mecânica do sistema a esta baixa frequência é conforme ou semelhante a uma mola. Acústicamente, parece uma conformidade acústica: empurramos a massa de ar no pescoço e comprimimos o ar no ressonador. A força F aplicada à direita está em fase com x medida à direita, portanto está 90° atrás da velocidade e a pressão aplicada está 90° atrás do fluxo acústico para dentro do ressonador.
Lembrar que f2 depende da aceleração. Assim, a uma frequência suficientemente alta, a força da mola é insignificante em comparação com aquela que acelera a massa. Assim, F está em fase com a aceleração, o que a coloca 90° à frente da velocidade. Acústicamente, a pressão aplicada está 90° à frente do fluxo acústico para o ressonador. É uma inércia mecânica ou acústica.
Na freqüência ressonante (ainda falando do esboço acima), a amplitude pode ser grande para uma força muito pequena. Assim, na ressonância, a impedância é muito baixa, quando vista a partir da força aplicada à massa a partir do exterior (o diagrama acima). Na ressonância, há um fluxo máximo para dentro e para fora do ressonador.
Agora considere o que acontece se observarmos a pressão dentro do ressonador (longe do pescoço). Aqui estamos olhando para a força na mola, então o nosso análogo mecânico se parece com este esquema.
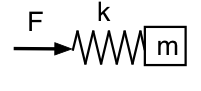
Esta vez, baixa frequência significa que a força pode ser pequena para uma dada amplitude: a mola e a massa movem-se juntas como uma massa, e o sistema desta vez parece inerte a baixa frequência. Em alta freqüência, a massa dificilmente se move, e o sistema é tipo mola ou complacente. Portanto, as relações de fase são opostas ao que tínhamos antes: em baixa f, p leva U por 90°; em alta f, p p fica U por 90°.
Complicações envolvendo o comprimento efectivo
O primeiro diagrama desta página desenha o ‘tampão’ de ar como se fosse uma garrafa que termina ordenadamente em ambas as extremidades do gargalo da garrafa. Isto é super simplificado. Na prática, um volume extra tanto dentro como fora se move com o ar no gargalo – como sugerido na animação acima. O comprimento extra que deve ser adicionado ao comprimento geométrico do gargalo é tipicamente (e muito aproximadamente) de 0,6 vezes o raio na extremidade externa, e um raio na extremidade interna).
|
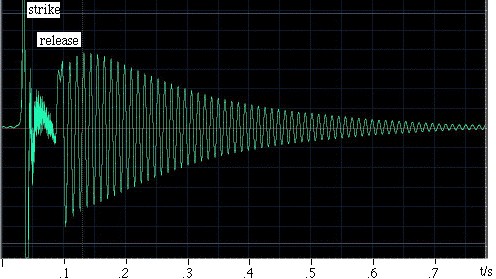
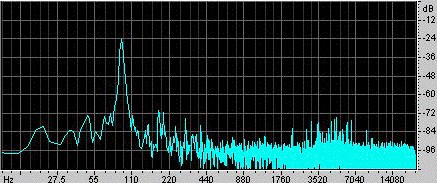
Um exemplo. Ra Inta fez este exemplo. Ele pegou um ressonador Helmholtz esférico com um volume de 0,00292 m3 e um pescoço cilíndrico com comprimento de 0,080 m e área de secção transversal de 0,00083 m2. Para excitá-lo, ele o atingiu com a palma da mão e depois o soltou. Um microfone dentro do ressonador grava o som, que é mostrado no oscilograma à esquerda. Você pode ver que a mão sela o ressonador por menos de 0,1 s, e que durante esse tempo as oscilações são mais fracas e de freqüência relativamente alta. Após a mão ser libertada, estabelece-se uma oscilação, que vai desaparecendo gradualmente à medida que perde energia por arrasto viscoso e turbulento, e também por radiação sonora. Um exame atento mostra que a frequência aumenta ligeiramente à medida que a mão se afasta da extremidade aberta, porque isto a mão restringe o ângulo sólido disponível para a radiação e assim aumenta o efeito final (ou correcção final). O comprimento do pescoço é aumentado em um efeito final batido e um efeito final não batido, dando-lhe um comprimento efectivo de 0,105 m. Com uma velocidade do som de 343 m/s, a expressão acima dá uma frequência ressonante de 90 Hz. |
|
Ressonâncias e guitarras de Helmholtz
* Eu disse acima que o ar no corpo de uma guitarra age quase como um oscilador de Helmholtz. Este caso é complicado porque o corpo pode inchar um pouco quando a pressão do ar sobe dentro – e também porque o ar ‘dentro’ do buraco do som da guitarra tem uma geometria que é menos facilmente visualizada do que a do gargalo de uma garrafa. Na verdade, no caso do corpo da guitarra, o comprimento da tomada de ar é aproximadamente igual aos dois “efeitos finais” na extremidade de um “tubo” que tem apenas um par de mm de espessura. Os efeitos finais, no entanto, estão relacionados e são de tamanho semelhante ao raio do buraco, pelo que a massa de ar é substancial. O comprimento do efeito final de um tubo cilíndrico que se abre para um abafador plano infinito é 0,85 vezes o raio do tubo. Embora a mesa de som de uma guitarra não seja infinita, seria de esperar um efeito final semelhante, e assim o comprimento efectivo do ‘tampão’ de ar seria cerca de 1,7 vezes o raio do furo. (Alguns fabricantes aumentam isto fixando um tubo curto abaixo da caixa de som, com raio igual).
Um par de pessoas tem escrito perguntando quão grande deve ser o furo de som para um determinado instrumento. Bem, podemos usar a equação acima para começar a responder a essa pergunta. No entanto, o inchaço do corpo é importante. Isto torna a ‘mola’ do ar bastante mais suave e diminui a frequência. A ressonância puramente Helmholtz pode ser investigada mantendo o volume do corpo constante. Ao medir isto, uma prática comum é enterrar a guitarra na areia, para impedir o inchaço ou a “respiração” do corpo. No entanto, as guitarras não são normalmente tocadas nesta situação. Assim, o cálculo do Helmholtz dará uma superestimativa da frequência de ressonância para um corpo real e flexível.
Vamos assumir um furo de som circular com raio r, então S = πr2, e L = 1.7r como explicado acima. Quando substituímos na equação a frequência de Helmholtz, usando c = 340 m/s, obtemos:
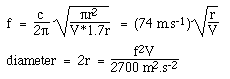 Note que estamos usando unidades SI padrão: usamos a velocidade do som em metros e segundos, então o volume deve estar em metros cúbicos e a freqüência em Hertz, para dar uma resposta em metros.
Note que estamos usando unidades SI padrão: usamos a velocidade do som em metros e segundos, então o volume deve estar em metros cúbicos e a freqüência em Hertz, para dar uma resposta em metros.
É mais complicado quando os furos de tom não são circulares, porque o efeito final não é igual ao de um círculo com a mesma área. O estudante de doutorado e luthier John McLennan está escrevendo um relatório de algumas medidas sobre isso, que publicaremos aqui em breve.
Em instrumentos de guitarra e violino da família Helmholtz (mais corpo), a ressonância Helmholtz (mais corpo) está frequentemente próxima ou um pouco abaixo da frequência da segunda corda mais baixa, em torno de D em um violino ou G-A em um violão. Você pode reduzir ou mudar substancialmente a freqüência do Helmholtz cobrindo todo ou parte do buraco com um pedaço de papelão rígido com a forma adequada. Se você tocar uma nota perto da ressonância e depois deslizar a carta de modo que ela cubra e revele o buraco alternadamente, você ouvirá claramente o efeito da ressonância.
O efeito 0,85r é razoável? Ra Inta, que fez um doutorado em acústica de guitarra no nosso laboratório, sugere uma demonstração interessante:
Ampare as cordas na sua guitarra para que elas não vibrem (por exemplo, um lenço entre as cordas e a placa do dedo). Segure a palma de uma mão acima do orifício de som, e próximo a ele. Com um dedo da outra mão, golpeie a mesa de som com um golpe agudo perto da caixa de ressonância e perto da 1ª corda. Você sentirá um pulso de ar na palma da sua mão. O golpe do seu dedo empurra a mesa de som para dentro e aperta um pouco de ar para fora do corpo. Agora afaste gradualmente a sua mão do buraco e continue a bater com o dedo. Quando você deixa de sentir o movimento do ar? Isso lhe dará uma estimativa aproximada da duração do “efeito final” no caso do buraco sonoro.
Afinando a ressonância do Helmholtz
Entre as publicações de John McLennan, aluno de doutorado neste laboratório, está um artigo no qual ele varia a ressonância do Helmholtz variando a velocidade do som.
- McLennan, J.E. (2003) “A0 and A1 studies on the violin using CO2, He, and air/helium mixtures”. Acustica, 89, 176-180.
Algumas fotos de ressonadores históricos de Helmholtz fornecidas por Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply