Articles /

Processo Gram-Schmidt

por Marco Taboga, PhD

O processo (ou procedimento) Gram-Schmidt é uma seqüência de operações que permite transformar um conjunto de vetores linearmente independentes em um conjunto de vetores orto-normais que abrangem o mesmo espaço abrangido pelo conjunto original.

Tabela de conteúdos

Preliminares

Vamos rever algumas noções que são essenciais para entender o processo Gram-Schmidt.

Lembrem-se que dois vetores $r$ e $s$ são ditos ortogonais se e somente se seu produto interno for igual a zero, ou seja,

Dado um produto interno, podemos definir a norma (comprimento) de um vetor $s$ da seguinte forma

Um conjunto de vectores é chamado orthonormal se e só se os seus elementos tiverem uma norma unitária e forem ortogonais uns aos outros. Em outras palavras, um conjunto de K vectores é orthonormal se e somente se

Provamos que os vectores de um conjunto orthonormal são linearmente independentes.

Quando uma base para um espaço vectorial é também um conjunto orthonormal, ele é chamado de base orthonormal.

Projeções em conjuntos orthonormais

No processo Gram-Schmidt, usamos repetidamente a próxima proposta, que mostra que cada vetor pode ser decomposto em duas partes: 1) sua projeção em um conjunto orthonormal e 2) um residual que é ortogonal ao conjunto orthonormal dado.

Proposição Vamos $S$ ser um espaço vetorial equipado com um produto interno . Que seja um conjunto orthonormal. Para qualquer $$sin S$, temos onde $arepsilon _{S}$ é ortogonal a $u_{k}$ para qualquer $k=1,ldots ,K.$

Proof

DefinirEntão, para cada $j=1,ldots ,K$, temos issoem qualquer lugar: nos passos $rame{A}$ e $rame{B}$ usamos o fato de que o produto interno é linear em seu primeiro argumento; no passo $rame{C}$ usamos o fato de que if $keq j$ já que estamos lidando com um conjunto orthonormal; no passo $rame{D}$ usamos o fato de que a norma de $u_{j}$ é igual a 1. Portanto, $arepsilon _{S}$, como definido acima, é ortogonal a todos os elementos do conjunto orthonormal, o que prova a proposição.

O termo é chamado de projeção linear de $s$ no conjunto orthonormal , enquanto o termo $arepsilon _{S}$ é chamado de resíduo da projeção linear.

Normalização

Outro fato talvez óbvio que vamos usar repetidamente no processo Gram-Schmidt é que, se pegarmos qualquer vetor não-zero e o dividirmos por sua norma, então o resultado da divisão é um novo vetor que tem norma unitária.

Em outras palavras, se então, pela propriedade de definição da norma, temos que

Como consequência, podemos definir e, pela positividade e homogeneidade absoluta da norma, temos

Visão geral do procedimento

Agora que sabemos como normalizar um vector e como decompô-lo numa projecção num conjunto orto-normal e num residual, estamos prontos para explicar o procedimento Gram-Schmidt.

Vamos dar uma visão geral do processo, após o que o expressaremos formalmente como uma proposta e discutiremos todos os detalhes técnicos na prova da proposta.

Aqui está a visão geral.

Nos é dado um conjunto de vetores linearmente independentes .

Para iniciar o processo, normalizamos o primeiro vector, ou seja, definimos

No segundo passo, projectamos $s_{2}$ em $u_{1}$: onde $arepsilon _{2}$ é o resíduo da projecção.

Então, normalizamos o residual:

Mais tarde provaremos que (para que a normalização possa ser feita) porque os vetores de partida são linearmente independentes.

Os dois vetores $u_{1}$ e $u_{2}$ assim obtidos são orthonormais.

No terceiro passo, projetamos $s_{3}$ em $u_{1}$ e $u_{2}$: e calculamos o resíduo da projeção $arepsilon _{3}$.

Depois normalizamos:

Procedemos desta forma até obter o último residual normalizado $u_{K} $.

Ao final do processo, os vetores formam um conjunto orto-normal porque:

  1. são o resultado de uma normalização, e como conseqüência têm norma unitária;

  2. cada $u_{k}$ é obtido de um resíduo que tem a propriedade de ser ortogonal a .

Para completar esta visão geral, lembremos que o intervalo linear de é o conjunto de todos os vectores que podem ser escritos como combinações lineares de ; é denotado por e é um espaço linear.

Uma vez que os vectores são combinações linearmente independentes de , qualquer vector que possa ser escrito como uma combinação linear de também pode ser escrito como uma combinação linear de . Portanto, os intervalos dos dois conjuntos de vetores coincidem:

Declaração formal

Formalizamos aqui o processo Gram-Schmidt como uma proposta, cuja prova contém todos os detalhes técnicos do procedimento.

Proposição Let $S$ ser um espaço vetorial equipado com um produto interno . Deixar ser vectores linearmente independentes. Então, existe um conjunto de vectores orto-normais tal que para qualquer $kleq K$.

Prova

A prova é por indução: primeiro provamos que a proposta é verdadeira para $k=1$, e depois provamos que é verdadeira para um genérico k se for válida para $k-1$. Quando $k=1$, o vector tem uma norma unitária e constitui por si só um conjunto orthonormal: não existem outros vectores, pelo que a condição de ortogonalidade é trivialmente satisfeita. O conjunto é o conjunto de todos os múltiplos escalares de $s_{1}$, que também são múltiplos escalares de $u_{1}$ (e vice versa). Portanto, Agora, suponha que a proposta seja verdadeira para $k-1$. Então, podemos projetar $s_{k}$ em : onde o residual $arepsilon _{k}$ é ortogonal para . Suponha que $arepsilon _{k}=0$. Então,Desde que, por suposição, para qualquer $jleq k-1$, temos que para qualquer $jleq k-1$, onde $lpha _{jl}$ são escalares. Portanto,Em outras palavras, a hipótese de que $arepsilon _{k}=0$ leva à conclusão de que $s_{k}$ é uma combinação linear de . Mas isto é impossível porque uma das hipóteses da proposta é que são linearmente independentes. Como consequência, deve ser que . Podemos portanto normalizar o residual e definir o vetor que tem norma unitária. Já sabemos que $arepsilon _{k}$ é ortogonal a . Isto implica que também $u_{k}$ é ortogonal a . Assim, é um conjunto orthonormal. Agora, pegue qualquer vetor $sin S$ que pode ser escrito como onde são escalares. Como, por suposição, temos essa equação (2) também pode ser escrita como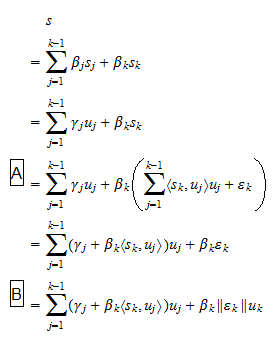 onde são escalares, e: no passo $rame{A}$ usamos a equação (1); no passo $rame{B}$ usamos a definição de $u_{k}$. Assim, provamos que todo vetor que pode ser escrito como uma combinação linear de também pode ser escrito como uma combinação linear de . Assumir (3) permite provar o inverso de uma maneira completamente análoga: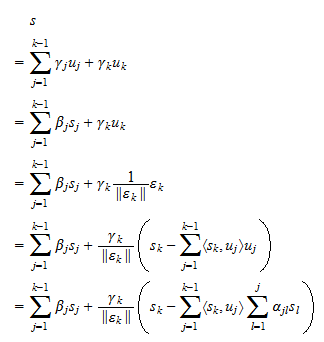 Em outras palavras, cada combinação linear de é também uma combinação linear de . Isto prova que e conclui a prova.

Cada espaço interior do produto tem uma base orto-normal

A seguinte proposta apresenta uma importante consequência do processo Gram-Schmidt.

Posição Que $S$ seja um espaço vectorial equipado com um produto interior . Se $S$ tem dimensão finita , então existe uma base orthonormal para $S$.

Prova

Desde que $S$ seja de dimensão finita, existe pelo menos uma base para $S$, constituída por K vectores . Podemos aplicar o procedimento Gram-Schmidt à base e obter um conjunto orthonormal . Como é uma base, ela abrange $$. Portanto, 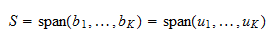Assim, é uma base orto-normal de $S$.

>

>

Exercícios resolvidos

Abaixo você pode encontrar alguns exercícios com soluções explicadas.

Exercício 1

Considere o espaço $S$ de todos $3 vezes 1$ vectores com entradas reais e o produto interno onde $r,sin S$ e $s^{op }$ é a transposição de $s$. Define o vector

Normalizar $s$.

Solução

A norma de $s$ éPor isso, a normalização de $s$ é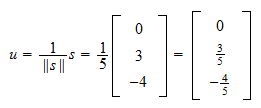

Exercício 2

Considere o espaço $S$ de todos $2 vezes 1$ vetores com entradas reais e o produto interno onde $r,sin S$ . Considere os dois vetores linearmente independentes

Transforme-os em um conjunto orthonormal usando o processo Gram-Schmidt.

Solução

A norma de $s_{1}$ é Por isso, o primeiro vector orthonormal éO produto interior de $s_{2}$ e $u_{1}$ é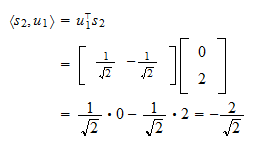A projecção de $s_{2}$ em $u_{1}$ é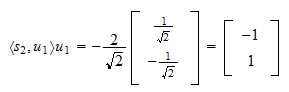O resíduo da projecção é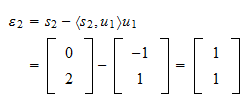A norma do resíduo ée o resíduo normalizado éAssim, o conjunto orthonormal que procurávamos é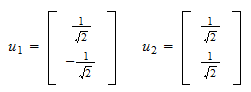

Como citar

Cite por favor como:

>

Taboga, Marco (2017). “Processo Gram-Schmidt”, Palestras sobre álgebra matricial. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply