Parte 14 : Produto Dot e Hadamard

Para além da multiplicação da matriz discutida anteriormente, os vectores poderiam ser multiplicados por mais dois métodos : Produto Dot e Produto Hadamard. Os resultados obtidos pelos dois métodos são diferentes.

Os elementos correspondentes à mesma linha e coluna são multiplicados juntos e os produtos são adicionados de tal forma que, o resultado é um escalar.

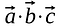
Multiplicação de matriz não semelhante ao produto de ponto, o resultado do produto de ponto não é outro vector ou matriz, é um escalar.

Ordem de vectores não importa para o produto ponto, apenas o número de elementos em ambos os vectores deve ser igual.

A fórmula geométrica do produto ponto é

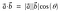
O produto ponto é também chamado produto interior ou produto escalar.

Projeção de Vetor

Assumindo que temos dois vetores c e d, subtendidos por ângulo, phi(Ф).

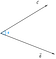
Agora, a projecção do vector c no vector d poderia ser representada como

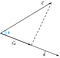
Podemos concluir pela figura que a projecção é igual à componente horizontal do vector c no que diz respeito ao ângulo phi(Ф).

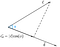
Chama-se projeção escalar.Para encontrar a projecção vectorial do vector c no vector d temos de multiplicar a projecção escalar pelo vector unitário d.

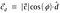
Substituindo o valor do vector unitário d.

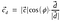
Assim, dot product também poderia ser representado como

Projeções têm amplo uso em álgebra linear e aprendizagem de máquina (Support Vector Machine(SVM) é um algoritmo de aprendizagem de máquina, usado para classificação de dados).

Produtoadamard (Element -wise Multiplication)

Produtoadamard de dois vectores é muito semelhante à adição de matrizes, elementos correspondentes à mesma linha e colunas de determinados vectores/matrizes são multiplicados em conjunto para formar um novo vector/matriz.

Tem o nome do matemático francês Jacques Hadamard.

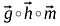
A ordem das matrizes/vetores a serem multiplicados deve ser a mesma e a matriz resultante também será da mesma ordem.

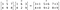
Produto Hadamard é usado em técnicas de compressão de imagem como o JPEG. É também conhecido como produto Schur depois do matemático alemão Issai Schur.

O produto Hadamard é usado em células LSTM (Long Short-Term Memory) de Redes Neurais Recorrente (RNNs).