O que é a Geometria Analítica?
O que é a Geometria Analítica?
A Geometria Analítica é um ramo de álgebra que é usado para modelar objetos geométricos – pontos, linhas (retas), e círculos sendo o mais básico destes. A geometria analítica é uma grande invenção de Descartes e Fermat.
Na geometria analítica plana, os pontos são definidos como pares ordenados de números, digamos, (x, y), enquanto as retas são por sua vez definidas como os conjuntos de pontos que satisfazem equações lineares, veja as excelentes exposições de D. Pedoe ou D. Brannan et al. Do ponto de vista da geometria analítica, os axiomas geométricos são teoremas deriváveis. Por exemplo, para quaisquer dois pontos distintos (x1, y1) e (x2, y2), há um único eixo linear + por + c = 0 que passa por esses pontos. Seus coeficientes a, b, c podem ser encontrados (até um fator constante) do sistema linear de duas equações
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
ou directamente da equação determinante
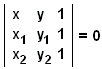 |
No entanto, nenhuma teoria axiomática pode escapar usando elementos indefinidos. Na Teoria dos Conjuntos que está subjacente a grande parte da matemática e, em particular, da geometria analítica, a noção mais fundamental de conjunto permanece indefinida.
A geometria do espaço tridimensional é modelada com triplos de números (x, y, z) e um eixo de equação linear 3D + por + cz + d = 0 define um plano. Em geral, a geometria analítica proporciona uma ferramenta conveniente para trabalhar em dimensões superiores.
No quadro da geometria analítica também se pode (e se faz) modelar geometrias não euclidianas. Por exemplo, em geometria projectiva plana um ponto é um triplo de coordenadas homogéneas (x, y, z), não todas 0, de tal forma que
| (tx, ty, tz) = (x, y, z), |
para todos t ≠ 0, enquanto uma linha é descrita por uma equação homogênea
| ax + bx + cz = 0. |
| ax² + bxy + cy² + dx + ey + f = 0, |
A parte da geometria analítica que lida principalmente com equações lineares chama-se Álgebra Linear.
A geometria analítica cartesiana é aquela em que os eixos x = 0 e y = 0 são perpendiculares.
Os componentes do n-tuplo x = (x1, …, xn) são conhecidos como suas coordenadas. Quando n = 2 ou n = 3, as primeiras coordenadas são chamadas abcissas e a segunda ordenada.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contact|||Front page|||Conteúdo|||Geometry|||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply