Matemática para as Artes Liberais
Realizações de Aprendizagem
- Definir e identificar a auto-similaridade em formas geométricas, plantas, e formações geológicas
- Gerar uma forma fractal dado um iniciador e um gerador
- Escalar um objecto geométrico por um factor de escala específico usando a relação de dimensão de escala
- Determinar a dimensão fractal de um objecto fractal
Além da auto-similaridade visual, os fractais exibem outras propriedades interessantes. Por exemplo, observe que cada passo da iteração da junta Sierpinski remove um quarto da área restante. Se este processo for continuado indefinidamente, acabaremos essencialmente removendo toda a área, ou seja, começamos com uma área bidimensional, e de alguma forma acabamos com algo menos do que isso, mas aparentemente mais do que apenas uma linha unidimensional.
Para explorar esta idéia, precisamos discutir dimensão. Algo como uma linha é unidimensional; ela só tem comprimento. Qualquer curva é unidimensional. Coisas como caixas e círculos são bidimensionais, já que têm comprimento e largura, descrevendo uma área. Objetos como caixas e cilindros têm comprimento, largura e altura, descrevendo um volume, e são tridimensionais.
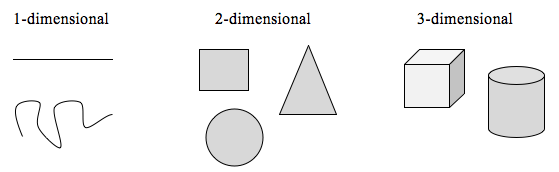
Regras certas se aplicam aos objetos de escala, relacionadas à sua dimensão.
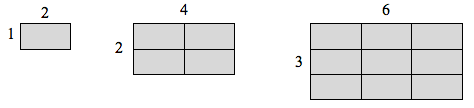
Se eu tivesse uma linha com comprimento 1, e quisesse escalar seu comprimento em 2, precisaria de duas cópias da linha original. Se eu tivesse uma linha com comprimento 1, e quisesse escalar o seu comprimento por 3, precisaria de três cópias do original.
Se eu tivesse um retângulo com comprimento 2 e altura 1, e quisesse escalar o seu comprimento e largura por 2, precisaria de quatro cópias do retângulo original. Se eu quisesse escalar o comprimento e a largura por 3, precisaria de nove cópias do retângulo original.
Se eu tivesse uma caixa cúbica com lados de comprimento 1, e quisesse escalar seu comprimento e largura por 2, eu precisaria de oito cópias do cubo original. Se eu quisesse escalar o comprimento e a largura por 3, precisaria de 27 cópias do cubo original.
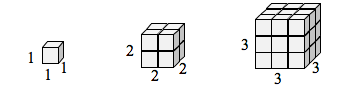
Notem que no caso tridimensional, cópias necessárias = escala.
No caso bidimensional, cópias necessárias = escala^{2}.
No caso tridimensional, cópias necessárias = escala^{3}.
Destes exemplos, podemos inferir um padrão.
Relação dimensional
Para dimensionar uma forma D-dimensional por um fator de escala S, o número de cópias C da forma original necessária será dado por:
\text{Copies}=\text{Scale}^{\text{Dimension}}, ou C=S^{D}
Exemplo
Utilizar a relação escala-dimensão para determinar a dimensão da junta Sierpinski.
>
Ponhamos que definimos a junta original para ter comprimento lateral 1. A junta maior mostrada é duas vezes mais larga e duas vezes mais alta, portanto foi escalada por um fator de 2,
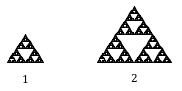
Notem que para construir a gaxeta maior, são necessárias 3 cópias da gaxeta original.
Usando a relação escala-dimensão C=S^{D}, obtemos a equação 3=2^{D}.
Desde 2^{1}=2 e 2^{2}=4, podemos ver imediatamente que D está algures entre 1 e 2; a junta é mais do que uma forma unidimensional, mas tirámos tanta área que agora é menos do que bidimensional.
Solucionar a equação 3=2^{D} requer logaritmos. Se você estudou logaritmos antes, você pode se lembrar como resolver esta equação (se não, basta pular para a caixa abaixo e usar essa fórmula com a chave log em uma calculadora):
Tirar o logaritmo de ambos os lados.
3={{{2}^{D}}
Utilizar a propriedade exponente dos logaritmos.
\log(3)={{2}^{D}}{Direita)
Dividir por log(2).
\log(3)=D\log(2)=Esquerda(2)
A dimensão da junta é cerca de 1.585.
D=frac{\log(3)}{\log(2)}approx1.585
Relação dimensional, para encontrar a dimensão
Para encontrar a dimensão D de um fractal, determinar o factor de escala S e o número de cópias C da forma original necessária, então use a fórmula
D=\frac{\log}esquerda(C\log(S)}
Try It
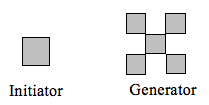
Determine a dimensão fractal do fractal produzido usando o iniciador e o gerador.
No vídeo seguinte, apresentamos um exemplo trabalhado de como determinar a dimensão da junta Sierpinski

Leave a Reply